Модуль random. Часть 1 | Программирование на Питоне

Все курсы > Программирование на Питоне > Занятие 11 (часть 1)

Библиотека Numpy предоставляет широкие возможности по работе со случайными числами. Для этого в ней предусмотрен модуль random.

Модуль random — это модуль, который позволяет генерировать псевдослучайные числа и таким образом имитировать случайные события.

При этом прежде чем перейти к изучению кода, давайте познакомимся с некоторыми ключевыми понятиями теории вероятностей.

Содержание занятия

Случайная величина

Рассмотрим некоторое событие (event) $A$, например, выпадение пятерки на игральной кости. Это событие случайно (random process), так как оно может произойти, а может не произойти.

Испытанием (trial) или экспериментом будет процесс бросания игральной кости, а элементарными исходами (outcomes) испытания $\omega_i$ («омега» малое) — возможные результаты, то есть грани с числами от одного до шести.

Совокупность элементарных исходов называется пространством элементарных исходов (sample space) $\Omega$ («омега» большое).

При этом случайная величина (random variable) $X$ — это численное значение результата испытания. Одновременно речь идет о функции $\xi$ («кси»), которая отображает множество элементарных исходов $\omega_i$ на некоторое числовое множество $x_i = \xi(\omega_i)$.

Вероятность случайной величины

Хотя по определению случайное событие предсказать нельзя, мы можем предположить, с какой вероятностью оно произойдет. Начнем с классического или как еще говорят теоретического определения вероятности.

Классическая (теоретическая) вероятность

Пусть $k$ — количество благоприятствующих событию A исходов (то есть исходов, которые влекут за собой наступление события $A$), а $n$ — общее количество равновозможных исходов, тогда теоретической вероятностью события $A$ будет

$$ P(A) = \frac{k}{n} $$

Разберем это определение на том же примере бросания игральной кости.

В частности, выпадение двойки или тройки благоприятствует (приводит к наступлению) случайного события $A$. Таких исходов два (либо двойка, либо тройка) и соответственно $k = 2$. Всего исходов шесть и вероятность их наступления одинакова (они равновозможны). Значит $n = 6$. Рассчитаем теоретическую вероятность такого события.

$$ P(A) = \frac{2}{6} = \frac{1}{3} $$

Аналогично, вероятность выпадения орла или решки на «честной» монете (fair coin) равна 1/2, а вероятность вытащить червы из колоды, в которой 36 карт, равна 9/36 или 1/4.

Вероятность любого события находится в диапазоне от 0 до 1. При этом событие с нулевой вероятностью называется невозможным, а с вероятностью равной единице — достоверным. В промежутке находятся случайные события.

Сумма вероятностей событий, образующих полную группу, всегда равна единице. Выпадение орла и выпадение решки образуют полную группу (других событий при подбрасывании монеты быть не может). Вероятность каждого из этих событий равна 1/2, сумма этих вероятностей — единице.

Относительная (эмпирическая) вероятность

Эмпирическая вероятность события — это отношение частоты наступления события А к общему числу испытаний. По большому счету, мы бросаем кости несколько раз и считаем, сколько раз выпала двойка или тройка по отношению к общему количеству бросков.

Предположим, мы бросали кость 10 раз и двойка или тройка выпали 4 раза. Рассчитаем эмпирическую вероятность такого события.

$$ P(A) = \frac{4}{10} = \frac{2}{5} $$

Испытаний (бросков) было проведено очень мало и эмпирическая вероятность довольно сильно отличается от теоретической. Что же будет, если кратно увеличить количество бросков?

Закон больших чисел

Закон больших чисел (Law of large numbers) утверждает, что при проведении множества испытаний эмпирическая вероятность начнет приближаться к теоретической. Другими словами, если бросать кость достаточное количество раз, то эмпирическая вероятность выпадения двойки или тройки приблизится к 1/3.

Откроем ноутбук к этому занятию⧉

Модуль random библиотеки Numpy

Начнем изучение модуля random с нескольких практических примеров. В частности посмотрим, как можно имитировать подбрасывание монеты и бросание игральной кости, убедимся в верности Закона больших чисел с помощью метода Монте-Карло, рассмотрим задачу о двух конвертах, а также познакомимся с методом случайных блужданий.

Подбрасывание монеты

Подбрасывание монеты можно имитировать, обозначив орел и решку через 0 и 1 и случайно генерируя соответствующие числа. Для этого подойдет функция np.random.randint().

На входе функция принимает границы диапазона (верхняя граница в диапазон не входит), на выходе — генерирует целые псевдослучайные числа в его пределах.

1 2	# при заданных границах от 0 до 2 функция генерирует 0 и 1 np.random.randint(0, 2)

Передав этой функции третий параметр, мы можем указать количество таких чисел.

1 2	# по сути, мы имитируем десять подбрасываний np.random.randint(0, 2, 10)

1	array([0, 1, 1, 0, 1, 1, 1, 1, 0, 0])

Бросание игральной кости

Бросание игральной кости можно имиритировать, изменив диапазон на [1, 7).

1 2	# аналогично имитируем десять бросков np.random.randint(1, 7, 10)

1	array([6, 4, 2, 6, 6, 5, 4, 5, 5, 1])

Метод Монте-Карло

Теперь давайте вернемся к Закону больших чисел. Для его проверки воспользуемся методом Монте-Карло.

Метод Монте-Карло позволяет исследовать какой-либо случайный процесс, многократно имитируя его с помощью компьютера.

В нашем случае мы будем многократно бросать игральную кость и для каждой серии испытаний рассчитывать эмпирическую вероятность выпадения двойки или тройки. Если с ростом количества испытаний в серии эмпирическая вероятность приблизится к теоретической, мы сможем подтвердить Закон больших чисел.

Будем создавать нашу программу поэтапно.

Шаг 1. Метод Монте-Карло

Вначале нам потребуется список серий с количеством испытаний в каждой из них. Причем для наглядности пусть количество испытаний от серии к серии увеличивается экспоненциально.

Создать такой список, вернее массив Numpy, можно с помощью функции np.logspace(). Она похожа на уже изученную нами функцию np.linspace() с той лишь разницей, что возвращает заданное количество чисел, которые равномерно распределены по логарифмической шкале в пределах заданного диапазона.

Пусть наша последовательность будет состоять из чисел 10, возведенных в степень от 1 до 6. То есть первым числом будет $10^1 = 10$, а последним $10^6 = 1 000 000$. Всего таких чисел будет 50 (значение функции np.logspace() по умолчанию).

# параметр dtype = 'int' позволит отбросить дробную часть

series = np.logspace(1, 6, dtype = 'int')

series

array([ 10, 12, 15, 20, 25, 32, 40,

51, 65, 82, 104, 132, 167, 212,

268, 339, 429, 542, 686, 868, 1098,

1389, 1757, 2222, 2811, 3556, 4498, 5689,

7196, 9102, 11513, 14563, 18420, 23299, 29470,

37275, 47148, 59636, 75431, 95409, 120679, 152641,

193069, 244205, 308884, 390693, 494171, 625055, 790604,

1000000])

Промежуточные числа Numpy рассчитает самостоятельно с помощью десятичного логарифма. Например, для получения числа 790604 мы возвели 10 в степень 5.897959007291967.

1	np.log10(790604)

1	5.897959007291967

Убедимся в верности вычислений.

1	10 ** np.log10(790604)

1	790604.0000000002

На графике такая последовательность демонстрирует экспоненциальный рост.

1	plt.plot(series)

Ровно то, что нам нужно.

Шаг 2. Напишем код для проведения испытаний

Используем два цикла:

С помощью первого (внешнего) цикла for мы можем имитировать серии бросков (всего 50 испытаний).
Второй (внутренний) цикл отвечает за броски каждой отдельной серии. В первый раз мы бросим кость 10 раз, во второй — 12 и так далее.

Пока ограничимся одной серией. Для этого в конце внешнего цикла поставим оператор break.

# обозначим точку отсчета

np.random.seed(42)

# во внешнем цикле пройдемся по сериям испытаний (их будет 50)

for i, trial in enumerate(series, 1):

# выведем серию и количество бросков внутри нее

print(f'Серия: {i}, количество испытаний: {trial}\n')

# во внутреннем цикле будем бросать кость

for n in range(trial):

# запишем результат каждого броска

result = np.random.randint(1, 7)

# выведем номер броска и соответствующий результат

print(f'Испытание: {n}, выпало число: {result}')

# прервемся после первой серии

break

Серия: 1, количество испытаний: 10

Испытание: 0, выпало число: 4

Испытание: 1, выпало число: 5

Испытание: 2, выпало число: 3

Испытание: 3, выпало число: 5

Испытание: 4, выпало число: 5

Испытание: 5, выпало число: 2

Испытание: 6, выпало число: 3

Испытание: 7, выпало число: 3

Испытание: 8, выпало число: 3

Испытание: 9, выпало число: 5

Шаг 3. Рассчитаем долю успешных испытаний

Создадим счетчик, в который будем записывать выпадения двойки или тройки. После окончания очередной серии испытаний разделим количество успешных бросков на общее количество испытаний.

# обозначим точку отсчета

np.random.seed(42)

# создадим счетчик для количества успешных испытаний

success = 0

# в двух циклах пройдемся по сериям и броскам в каждой серии

for trial in series:

for n in range(trial):

result = np.random.randint(1, 7)

# если результат будет равен двум или трем

if result == 2 or result == 3:

# обновим счетчик

success += 1

# в конце каждой серии посчитаем долю успешных испытаний

prob = success / trial

print(f'Серия: {i}\n') # и выведем номер серии,

print(f'Всего испытаний: {trial}') # общее количество испытаний,

print(f'Успешных исходов: {success}') # количество и

print(f'Эмпирическая вероятность: {prob}') # долю успешных испытаний

# прервемся после окончания первой серии

break

Серия: 1

Всего испытаний: 10

Успешных исходов: 5

Эмпирическая вероятность: 0.5

Обратите внимание, эмпирическая вероятность первой серии, в которой было только 10 бросков (1/2), далека от теоретической (1/3).

Шаг 4. Проведем полноценные испытания алгоритма

Теперь мы готовы протестировать наш алгоритм на всех 50-ти сериях. Дополним наш код списком, в который мы будем записывать долю успешных бросков (эмпирическую вероятность) в каждой серии.

Помимо этого будем замерять время исполнения кода с помощью магической команды %%time.

# замерим время исполнения ячейки

%%time

# обозначим точку отсчета

np.random.seed(42)

# создадим счетчик для испытаний в каждой серии

success = 0

# а также список для записи результатов в пределах одной серии

prob_list = []

# пройдемся по сериям

for trial in series:

# и броскам в каждой серии

for n in range(trial):

result = np.random.randint(1, 7)

# посчитаем количество успешных бросков

if result == 2 or result == 3:

success += 1

# вычислим долю успешных бросков

prob = success / trial

# добавим результат серии в список

prob_list.append(prob)

# обнулим счетчик для записи результата следующей серии

success = 0

# после проведения всех серий испытаний выведем их количество

print(f'Проведено серий испытаний: {len(prob_list)}')

# а также эмпирическую вероятность отдельных серий

print(f'Эмпирическая вероятность каждой пятой серии: {np.round(prob_list[::5], 2)}')

Проведено серий испытаний: 50

Эмпирическая вероятность каждой пятой серии: [0.5 0.22 0.34 0.37 0.34 0.33 0.34 0.34 0.33 0.33]

CPU times: user 21.5 s, sys: 51.1 ms, total: 21.5 s

Wall time: 26 s

Общее время выполнения кода составило 26 секунд.

Шаг 5. Оценим результат визуально

# зададим размер графика

plt.figure(figsize = (10, 8))

# выведем горизонтальную линию теоретической вероятности

plt.axhline(y = 1/3, c = 'r')

# а также эмпирическую вероятность по результатам 50-ти серий испытаний

plt.plot(prob_list)

# добавим подписи

plt.xlabel('Серии', fontsize = 16)

plt.ylabel('Вероятность', fontsize = 16)

plt.show()

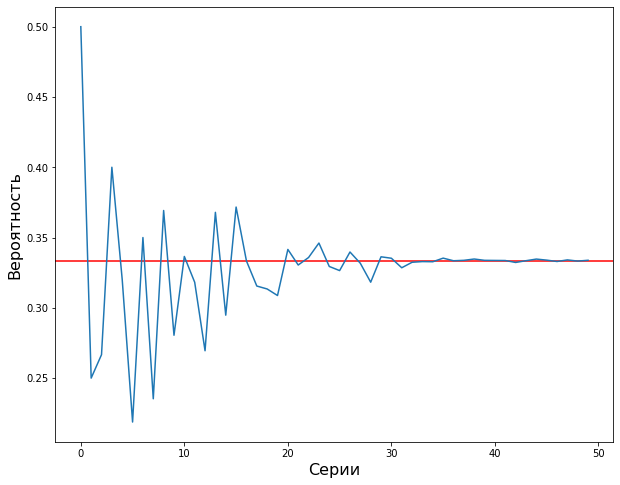
Как мы видим, если в первых сериях эмпирическая вероятность довольно сильно отличалась от теоретической, с увеличением количества бросков она вплотную приблизилась к 1/3.

Мы убедились в верности Закона больших чисел с помощью метода Монте-Карло.

Пример векторизованного кода

На прошлом занятии мы поговорили про векторизацию кода и выяснили, что векторизованный код исполняется быстрее, чем циклы for. Давайте посмотрим, нет ли возможности оптимизировать код с двумя циклами, написанный ранее.

%%time

np.random.seed(42)

# создадим новый список для записи результатов

prob_list_2 = []

# пройдемся по каждой из 50-ти серий

for trial in series:

# вместо второго цикла, передадим количество бросков

# непосредственно в функцию np.random.randint() через переменную trial

# и запишем полученные данные в массив result

result = np.random.randint(1, 7, trial)

# в переменную success запишем сумму выпавших двоек или троек из массива result

success = (result == 2).sum() + (result == 3).sum()

# посчитаем долю успешных исходов

prob = success / trial

# и запишем ее в список

prob_list_2.append(prob)

1 2	CPU times: user 77.1 ms, sys: 8.99 ms, total: 86 ms Wall time: 87.1 ms

Векторизованный код исполнился за 87,1 миллисекунды, то есть почти в 321 раз (26/0,081) быстрее, чем без использования векторизации.

Убедимся, что результат идентичен.

1 2	# разумеется, он будет одинаковым, если задать одну и ту же точку отсчета prob_list == prob_list_2

True

Задача о двух конвертах

Задача о двух конвертах (two envelopes problem) — популярная задача из области теории вероятностей. Сегодня мы рассмотрим один из ее вариантов и смоделируем решение с помощью модуля random.

Представьте, что вам дали конверт A, вы открыли его и увидели сумму X. После этого вам предлагают заменить этот конверт на другой конверт B, сумма в котором с одинаковой вероятностью либо в два раза меньше, либо в два раза больше суммы X. Стоит ли вам заменить конверт с A на B?

Аналитическое решение

Решим задачу аналитически. Пусть суммы в конверте B могут быть равны X/2 и 2X, тогда в среднем результат замены конвертов составит

$$ \frac{1}{2} \left( \frac{X}{2} \right) + \frac{1}{2} \left( 2X \right) = \frac{5}{4}X $$

Это больше, чем изначальная сумма X в конверте A, а значит нам стоит взять конверт B.

Теперь рассмотрим конкретный пример. Предположим, что в открытом нами конверте A было 5000 рублей, тогда в среднем при замене конвертов мы получим

$$ \frac{1}{2} \left( \frac{5000}{2} \right) + \frac{1}{2} \left( 2 \cdot 5000 \right) = \frac{5}{4} \cdot 5000 = 6250 $$

Моделирование с помощью модуля random

Проверим это решение с помощью Питона и Закона больших чисел.

# зададим точку отсчета и

np.random.seed(50)

# количество испытаний

trials = 100000

# создадим список для записи результатов

outcomes = []

# с помощью цикла for

for trial in range(trials):

# будем с одинаковой вероятностью генерировать числа 0 и 1

outcome = np.random.randint(0, 2)

# если выпадет ноль, то мы получим 2500 рублей

if outcome == 0:

# запишем этот результат в список

outcomes.append(2500)

else:

# в противном случае, запишем 10000

outcomes.append(10000)

# посчитаем среднее значение

sum(outcomes)/len(outcomes)

6249.475

Как мы видим, компьютер подтвердил, что в среднем (при достаточном количестве испытаний) будет выгоднее заменить конверт A на конверт B.

Парадокс двух конвертов

Добавлю, что если изменить условие задачи и не открывать конверт A, то задача превратится в парадокс двух конвертов (two envelopes paradox). Ведь если в среднем выгоднее заменить конверт A на B, то будет выгодно и обратное действие (заменить B на A).

Такой обмен конвертами может длиться бесконечно, а это приводит к противоречию поскольку выше мы доказали, что изначальная замена конверта A на B более выгодна.

Рассмотрение этого парадокса выходит за рамки сегодняшнего занятия.

Метод случайных блужданий

Генератор случайных чисел также применяется в так называемом методе случайных блужданий (random walk models, random walkers). С его помощью мы можем конструировать путь, состоящий из последовательности случайных шагов в определенном пространстве и, таким образом, моделировать различные процессы.

Случайное блуждание по числовой прямой

В самом простом варианте мы будем подбрасывать монету и смотреть, куда мы сдвинулись относительно предыдущего шага на числовой прямой. Посмотрим на алгоритм.

# поставим точку отсчета

np.random.seed(2)

# создадим список и запишем в него исходную позицию

moves = [0]

# для наглядности запишем результат бросания монеты

coins = []

for x in range(5):

# в цикле подбросим монету

coin = np.random.randint(0, 2)

# если выпадет 1, сдвинемся на одно значение от предыдущего результата

# если выпадет 0, останемся на месте

# запишем результат в список moves

moves.append(moves[x] + coin)

# также запишем результат подбрасывания монеты

coins.append(coin)

Выведем сделанные шаги.

moves

1	[0, 0, 1, 2, 2, 2]

И то, какой результат мы получали при подбрасывании монеты.

coins

1	[0, 1, 1, 0, 0]

Для наглядности давайте посмотрим на сделанные шаги на числовой прямой.

Начальное положение ($s_0$) находится в точке ноль. При первом подбрасывании монеты выпадает 0, и на первом шаге ($s_1$) мы остаемся на месте. На втором шаге ($s_2$) выпадает единица, и мы сдвигаемся в точку один. На третьем шаге ($s_3$) мы перемещаемся в точку два. После этого, на шагах четыре ($s_4$) и пять ($s_5$) мы остаемся на месте.

Доедем ли мы из Москвы до Санкт-Петербурга

метод случайных блужданий: путь от Москвы до Санкт-Петербурга

Теперь усложним задачу и посмотрим, сможем ли мы добраться из Москвы до Санкт-Петербурга на довольно необычном транспортном средстве, движение которого зависит от бросания игральной кости. Условия следующие:

Нам нужно преодолеть ровно 700 километров;
Если при бросании кости выпадет единица или двойка, мы сместимся на 5 километров вперед;
Если тройка или четверка, то на 5 километров назад;
В случае если выпадет пять или шесть, мы повторно бросим кость и сдвинемся на выпавшее число километров умноженное на пять;
Кроме того, есть вероятность внезапной поломки. Она составляет менее 0,001, то есть менее 0,1%. В этом случае на эвакуаторе нас отвезут обратно в Москву для ремонта.

Дополнительно договоримся, что в обратном направлении мы двигаться не можем, то есть если нам будет все время не везти, в минус мы не уйдем, число пройденных километров не должно быть отрицательным.

Теперь давайте с помощью Питона построим такой механизм.

Как уже было сказано, для бросания игральной кости мы будем использовать функцию np.random.randint() с параметрами 1 и 7.
Для того чтобы не уйти в минус, используем функцию max(). Первым параметром передадим 0, вторым — километр, на котором мы окажемся, если сдвинемся назад (то есть если выпадет твойка или четверка). В случае если второе число окажется отрицательным, то функция max() выберет ноль.
Поломку мы будем имитировать с помощью функции np.random.rand(). Эта функция генерирует равномерное распределение (об этом ниже) чисел в интервале [0, 1) и, если выпавшее число меньше, чем 0,001, мы вернемся в начало пути.

Посмотрим на код.

Функция случайного блуждания

# объявим функцию random_walk()

def random_walk():

# создадим список для записи перемещений от Москвы до Санкт-Петербурга

random_walk = [0]

# в цикле из 100 итераций

for m in range(99):

# запишем последний достигнутый километр в переменную move

move = random_walk[-1]

# бросим кость

dice = np.random.randint(1, 7)

# если выпадет 1 или 2, сместимся на пять вперед

if dice <= 2:

move = move + 5

# если выпадет 3 или 4, на пять назад, но в любом случае остановимся на нуле

elif dice <= 4:

move = max(0, move - 5)

# если выпадет 5 или 6, бросим кость еще раз и умножим результат на пять,

# это и будет следующее перемещение

else:

move = move + 5 * np.random.randint(1, 7)

# в случае внезапной поломки вернемся на нулевой километр

if np.random.rand() < 0.001:

move = 0

# запишем каждое движение в список random_walk

random_walk.append(move)

# вернем этот список при вызове функции

return random_walk

Создание одного случайного блуждания

Вызовем эту функцию для генерации одного случайного блуждания.

# зададим точку отсчета

np.random.seed(42)

# вызовем функцию random_walk() и поместим результат в переменную rw

rw = random_walk()

Выведем результат с помощью графика.

Посмотрим на расстояние, которое удалось преодолеть.

rw[-1]

430

Очевидно в этот раз мы не смогли доехать до Санкт-Петербурга.

Моделирование нескольких случайных блужданий

Давайте посмотрим на то, какова вероятность в среднем преодолеть этот путь.

# установим точку отсчета

np.random.seed(42)

# создадим список, в который будем помещать отдельные случайные блуждания

all_walks = []

# в цикле из 1000 итераций

for w in range(1000):

# сгенерируем случайное блуждание

rw = random_walk()

# и поместим его в список all_walks

all_walks.append(rw)

В переменной all_walks содержится список из списков. Преобразуем его в массив Numpy и транспонируем, чтобы отдельные случайные блуждания стали столбцами.

1 2	all_walks_T = np.array(all_walks).T all_walks_T.shape

1	(100, 1000)

Для наглядности мы можем использовать DataFrame библиотеки Pandas.

# импортируем библиотеку Pandas

import pandas as pd

# используем функцию pd.DataFrame()

df = pd.DataFrame(all_walks_T)

# и выведем последние пять строк

df.tail()

Первый столбец соответствует первому случайному блужданию и на шаге 100 (с индексом 99) мы достигли 430-ого километра.

Выведем результат на графике.

# зададим размер графика

plt.figure(figsize = (10, 8))

# и выведем каждое 30-ое блуждание

plt.plot(all_walks_T[:,::30])

# добавим подписи

plt.xlabel('Бросание кости', fontsize = 16)

plt.ylabel('Пройденный путь, км', fontsize = 16)

plt.show()

Обратите внимание на «упавшие» кривые. Это как раз те случаи, когда наше воображаемое транспортное средство ломалось, и мы возвращались в Москву на ремонт.

Вероятность преодоления пути

Теперь давайте возьмем достигнутые конечные точки каждого из 1000 испытаний и посмотрим на их распределение с помощью гистограммы.

# возьмем последнюю строку нашего массива

ends = all_walks_T[-1,:]

# и построим гистограмму с помощью plt.hist()

plt.hist(ends)

plt.show()

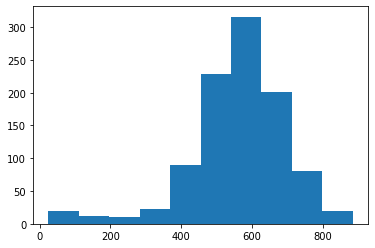
несколько случайных блужданий (гистограмма)

Выясним, какое расстояние в среднем проезжало наше транспортное средство.

1	ends.mean()

561.415

Кроме того, мы можем рассчитать вероятность преодоления 700 км. Для этого с помощью функции np.count_nonzero() рассчитаем количество блужданий, преодолевших расстояние между двумя столицами, и разделим получившийся результат на общее количество испытаний.

1	np.count_nonzero(ends >= 700)/len(ends)

0.128

Транспортное средство не слишком надежно, лишь в 12,8% случаев мы доезжали до конечной точки.

Продолжим знакомиться с теорией вероятностей и параллельно изучать возможности модуля random.