Все курсы > Программирование на Питоне > Занятие 9

Первое знакомство с библиотекой NumPy (Numerical Python) состоялось на двенадцатом занятии вводного курса. Затем мы несколько раз использовали эту библиотеку при построении моделей. Пришло время посвятить ее функционалу отдельный раздел.
Библиотека Numpy является основой для многих других библиотек в Питоне, например, Pandas, Matplotlib, scikit-learn или scikit-image. Главный объект библиотеки — массив Numpy (Numpy array). О нем мы поговорим сегодня.
На следующем занятии мы изучим математические операции над массивами, а через одно — рассмотрим работу со случайными числами.
Понятие массива Numpy
Массив Numpy — это многомерный массив (ndarray, n-dimensional array) данных, над которыми можно быстро и эффективно выполнять множество математических, статистических, логических и других операций.
Приведу пример массива с нулевым измерением, а также одно-, двух- и трехмерного массивов.

Теперь посмотрим как работать с этими массивами на практике.
Откроем ноутбук к этому занятию⧉
Вначале нужно импортировать библиотеку Numpy.
|
1 2 |
# библиотеку Numpy принято сокращать как np import numpy as np |
Как создать массив Numpy
Рассмотрим два варианта создания одномерного массива.
Функция np.array()
Во-первых, массив можно создать с помощью функции np.array(), которой мы передаем, например, список или кортеж элементов.
|
1 2 3 |
# создадим массив из списка arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) arr |
|
1 |
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) |
|
1 2 3 |
# или кортежа arr = np.array((0, 1, 2, 3, 4, 5, 6, 7, 8, 9)) arr |
|
1 |
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) |
Функция np.arange()
Кроме того, можно воспользоваться функцией np.arange(). Эта функция, как и функция range(), с которой мы уже знакомы, создает последовательность элементов. Обязательным параметром является верхняя граница, которая не входит в последовательность.
|
1 2 3 |
# создадим последовательность из 10 элементов arr = np.arange(10) arr |
|
1 |
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) |
Нижняя граница и шаг обязательными не являются.
|
1 2 3 |
# зададим нижнюю и верхнюю границу и шаг arr = np.arange(2, 10, 2) print(arr) |
|
1 |
array([2, 4, 6, 8]) |
Отличие range() от функции np.arange() заключается в том, что первая не допускает использования типа float.
|
1 2 |
# создадим список с помощью функций range() и list() list(range(2, 5.5, 0.5)) |

При этом в массиве Numpy тип float вполне может использоваться.
|
1 |
np.arange(2, 5.5, 0.5) |
|
1 |
array([2. , 2.5, 3. , 3.5, 4. , 4.5, 5. ]) |
Тип данных элементов массива
Как вы уже вероятно обратили внимание, в массивах тип данных определяется автоматически. При этом при создании массива мы можем задать этот параметр принудительно.
|
1 2 3 4 5 6 7 |
# создадим массив с элементами типа float arr_f = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], float) print(arr_f) # тип данных можно посмотреть через атрибут dtype print(arr_f.dtype) |
|
1 2 |
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] float64 |
Обратите внимание, в отличие, например, от списков, чаще всего в массивах содержатся элементы только одного типа (в частности, int или float).
Свойства (атрибуты) массива
Возьмем массив, который мы создали выше.
|
1 |
arr |
|
1 |
array([2, 4, 6, 8]) |
Важным свойством (или как правильнее говорить атрибутом) массива является количество его измерений, ndim. В данном случае это одномерный массив или вектор.
|
1 |
arr.ndim |
|
1 |
1 |
Теперь, с помощью атрибута shape, посмотрим на количество элементов в каждом измерении.
|
1 |
arr.shape |
|
1 |
(4,) |
Обратите внимание, даже когда массив одномерный, результат атрибута shape выводится в виде кортежа (на это указывают круглые скобки и запятая после цифры четыре).
Атрибут size показывает общее количество элементов во всех измерениях.
|
1 2 |
# пока что у нас одно измерение, в котором четыре элемента arr.size |
|
1 |
4 |
Как уже было сказано выше, атрибут dtype показывает тип данных отдельного элемента.
|
1 2 |
# в нашем случае - это целое число длиной 64 бита arr.dtype |
|
1 |
dtype('int64') |
Атрибут itemsize позволяет узнать размер в байтах (один байт состоит из 8 бит) одного элемента. В нашем случае, элемент (число) состоит из 64 бит, что составляет восемь байтов.
|
1 2 |
# 64 / 8 бит = 8 байтов arr.itemsize |
|
1 |
8 |
Общий размер массива в байтах (nbytes) позволяет понять, в частности, поместится ли массив в оперативную память компьютера.
|
1 2 |
# у нас четыре элемента по восемь байтов или 32 байта arr.nbytes |
|
1 |
32 |
Тот же результат можно получить, умножив общее количество элементов на размер одного элемента в байтах.
|
1 |
arr.size * arr.itemsize |
|
1 |
32 |
Измерения массива
Как уже было сказано, ndarray (массив Numpy) — это многомерный массив. Давайте еще раз взглянем на массивы с различными измерениями, добавив только что изученные атрибуты этих массивов.
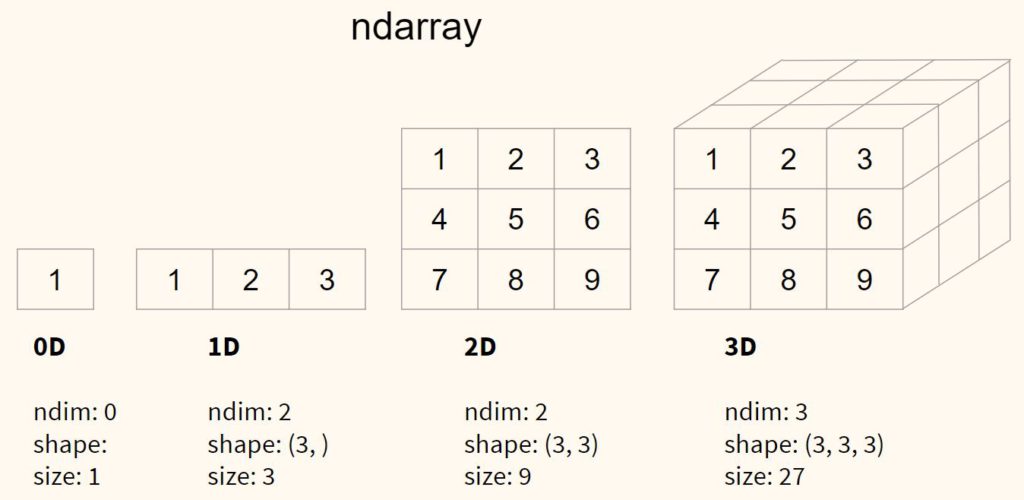
Теперь подробнее поговорим про размерность. Измерения (dimensions) создаются за счёт вложения одного массива в другой с помощью квадратных скобок []. Начнем с массива с нулевой размерностью.
Массив с нулевой размерностью
Массив с нулевой размерностью — это число (скаляр) и квадратных скобок не имеет.
|
1 2 |
arr_0D = np.array(42) arr_0D |
|
1 |
array(42) |
Посмотрим на свойства этого массива.
|
1 2 3 |
print(arr_0D.ndim) print(arr_0D.shape) print(arr_0D.size) |
Атрибут shape показывает отсутствие размерности, а size указывает на один элемент в массиве.
|
1 2 3 |
0 () 1 |
Одномерный массив (вектор)
Вложив несколько массивов с нулевой размерностью в квадратные скобки, мы получим одномерный массив или вектор.
|
1 2 |
arr_1D = np.array([1, 2, 3]) arr_1D |
|
1 |
array([1, 2, 3]) |
Снова воспользуемся атрибутами массива.
|
1 2 3 |
print(arr_1D.ndim) print(arr_1D.shape) print(arr_1D.size) |
|
1 2 3 |
1 (3,) 3 |
Двумерный массив (матрица)
Поместив во вторые квадратные скобки, например, два одномерных массива, мы получим двумерный массив или матрицу.
|
1 2 3 |
# с точки зрения синтаксиса - это просто вложенные списки arr_2D = np.array([[1, 2, 3], [4, 5, 6]]) arr_2D |
|
1 2 |
array([[1, 2, 3], [4, 5, 6]]) |
Посмотрим на свойства.
|
1 2 3 |
print(arr_2D.ndim) print(arr_2D.shape) print(arr_2D.size) |
|
1 2 3 |
2 (2, 3) 6 |
Атрибут size двумерного массива более интуитивно понятен. В данном случае два элемента одного измерения умножены на три элемента второго.
Добавлю, что с точки зрения Numpy матрица с одной строкой или одним столбцом — это разные объекты. Начнем с матрицы, которая имеет три вектора по одному элементу.
|
1 2 |
column = np.array([[1], [2], [3]]) column |
|
1 2 3 |
array([[1], [2], [3]]) |
|
1 2 |
# посмотрим на размерность column.shape |
|
1 |
(3, 1) |
Теперь наоборот, создадим матрицу с одной строкой, в которой три элемента.
|
1 2 |
row = np.array([[1, 2, 3]]) row |
|
1 |
array([[1, 2, 3]]) |
|
1 2 |
# размерность будет иной row.shape |
|
1 |
(1, 3) |
Трехмерный массив
Теперь создадим трехмерный массив, внутри которого будут два двумерных массива 2 х 3. Общее количество элементов будет равно двенадцати (2 х 2 х 3). Визуально это можно представить как стэк (наложение) двух матриц.

При этом, вместо того чтобы вручную прописывать все 12 значений, мы последовательно воспользуемся функцией np.arange() и методом np.reshape().
|
1 2 |
arr_3D = np.arange(12).reshape(2, 2, 3) arr_3D |
|
1 2 3 4 5 |
array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]]]) |
Функция np.arange(), как мы уже видели выше, создаст одномерный массив из 12 элементов, а метод np.reshape() распределит их по измерениям. Выведем атрибуты.
|
1 2 3 |
print(arr_3D.ndim) print(arr_3D.shape) print(arr_3D.size) |
|
1 2 3 |
3 (2, 2, 3) 12 |
Обратите внимание, атрибут shape сначала выводит размерность внешнего измерения, в нем две матрицы. Далее в каждую матрицу вложены два одномерных вектора. В каждом векторе по три элемента.
Аналогичным образом создаются четырехмерные массивы, а также массивы с большим количеством измерений.
Понятие тензора
Добавлю, что в математике n-мерный массив называется тензором, а числа (скаляры), векторы и матрицы являются его частными случаями для нуля, одного и двух измерений соответственно.

Другие способы создания массива
Массив из нулей
Иногда бывает полезно создать массив, все элементы которого равны нулю. Для этого используется функция np.zeros().
|
1 2 |
# ей мы можем передать одно значение для создания одномерного массива np.zeros(5) |
|
1 |
array([0., 0., 0., 0., 0.]) |
|
1 2 |
# или кортеж из чисел для указания количества нулей в каждом измерении np.zeros((2, 3)) |
|
1 2 |
array([[0., 0., 0.], [0., 0., 0.]]) |
Массив из единиц
В тех случаях когда нужно создать массив, заполненный единицами, можно воспользоваться функцией np.ones().
|
1 2 |
# создадим трехмерный массив np.ones((2, 2, 3)) |
|
1 2 3 4 5 |
array([[[1., 1., 1.], [1., 1., 1.]], [[1., 1., 1.], [1., 1., 1.]]]) |
Массив, заполненный заданным значением
Функция np.full() создает массив, заполненный заданным значением.
|
1 2 |
# создадим матрицу 2 х 3 и заполним ее цифрой четыре np.full((2, 3), 4) |
|
1 2 |
array([[4, 4, 4], [4, 4, 4]]) |
Пустой массив Numpy
В отличие от предыдущих инструментов, функция np.empty() возвращает массив заданной размерности, но без инициализации его значений. Другими словами, пустой массив.
|
1 2 |
# создадим пустую матрицу 3 х 2 np.empty((3, 2)) |
|
1 2 3 |
array([[4.65552661e-310, 0.00000000e+000], [0.00000000e+000, 0.00000000e+000], [0.00000000e+000, 0.00000000e+000]]) |
Кроме того, любой массив Numpy можно преобразовать в описанные выше массивы с помощью функций np.zeros_like(), np.ones_like(), np.full_like() и np.empty_like(). Приведу пример для np.zeros_like().
|
1 2 3 |
# создадим массив 2 x 3 с числами от 1 до 6 a = np.arange(1, 7).reshape(2, 3) a |
|
1 2 |
array([[1, 2, 3], [4, 5, 6]]) |
|
1 2 |
# и превратим его в массив с нулями np.zeros_like(a) |
|
1 2 |
array([[0, 0, 0], [0, 0, 0]]) |
Примеры работы с тремя оставшимися функциями можно посмотреть в ноутбуке⧉.
Функция np.linspace()
Функция np.linspace() позволяет указать диапазон начального и конечного значений, а также количество равноудаленных точек внутри этого диапазона (включая начальное и конечное значения).
|
1 2 3 |
# создадим диапазон от 0 до 0,9 и # разделим его на десять точек, включая 0 и 0,9 np.linspace(0, 0.9, 10) |
|
1 |
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]) |
Обратите внимание, функция np.linspace() сама определяет, где расставить точки. Нам нужно лишь указать их количество. Этим она отличается от функции np.arange(), в которой мы указываем шаг в пределах заданного диапазона.
|
1 2 |
# с функцией np.arange мы точно знаем, где будут расположены точки np.arange(0, 1, 0.1) |
|
1 |
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]) |
Функцию np.linspace() удобно использовать для построения графиков функций.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# импортируем библиотеку matplotlib import matplotlib.pyplot as plt # зададим размер графика в дюймах plt.figure(figsize = (8, 6)) # зададим интервал, например, от -5 до 5 и сформируем на нем 5000 точек # это будут наши координаты по оси x x = np.linspace(-5, 5, 5000) # по оси y отложим квадрат этих точек y = x ** 2 # создадим сетку plt.grid() # выведем кривую и подписи на графике plt.plot(x, y) plt.xlabel('x', fontsize = 14) plt.ylabel('y', fontsize = 14) # результатом будет парабола plt.show() |

В качестве примера выведем первые 10 точек, созданные функцией np.linspace().
|
1 |
x[:10] |
|
1 2 |
array([-5. , -4.9979996, -4.9959992, -4.9939988, -4.9919984, -4.989998 , -4.9879976, -4.9859972, -4.9839968, -4.9819964]) |
Функции np.random.rand() и np.random.randint()
Массивы можно также создавать с помощью функций, генерирующих псевдослучайные числа. В частности, функция np.random.rand() создает массив заданной размерности, заполненный числами от 0 до 1 (единица в диапазон не входит).
|
1 |
np.random.rand(4, 3) |
|
1 2 3 4 |
array([[0.13506003, 0.50671081, 0.48772983], [0.93478513, 0.31008048, 0.96621122], [0.7404316 , 0.81168816, 0.94700116], [0.18212183, 0.92247344, 0.2120635 ]]) |
Функция np.random.randint() формирует массив целых чисел в заданном диапазоне (верхняя граница не входит в диапазон) и с заданной размерностью.
|
1 2 |
# создадим массив размерностью 2 x 3 x 2 c числами [-3, 3) np.random.randint(-3, 3, size = (2, 3, 2)) |
|
1 2 3 4 5 6 7 |
array([[[-1, 0], [-1, 2], [-1, -1]], [[-2, 0], [ 0, 0], [-2, 1]]]) |
Более подробно с этими и другими похожими функциями мы познакомимся на одиннадцатом занятии.
Создание массива из функции
Помимо вышеупомянутых способов массив можно создавать с помощью собственных функций. Для того чтобы понять, как это работает, вначале давайте вспомним координаты массива Numpy.

Функция np.fromfunction() берет координаты (i, j) каждой ячейки и передает их в собственную функцию. Посмотрим, как это работает на практике.
|
1 2 3 4 |
# создадим собственную функцию, которая принимает два числа # и возводит первое число в степень второго def power(i, j): return i ** j |
Теперь применим эту функцию к каждой ячейке (координатам) массива с размерностью (3, 3).
|
1 |
np.fromfunction(power, (3, 3)) |
|
1 2 3 |
[[1. 0. 0.] [1. 1. 1.] [1. 2. 4.]] |
В np.fromfunction() можно передать и lambda-функцию.
|
1 2 3 |
# напишем lambda-функцию, которая принимает два числа и # проверяет равны ли они (тогда она выводит True) или нет (тогда False) lambda i, j : i == j |
|
1 2 3 |
array([[ True, False, False], [False, True, False], [False, False, True]]) |
Матрица csr и метод .toarray()
Кроме этого в случае если данные хранятся в формате csr (сжатое хранения строкой, compressed sparse row), то мы можем преобразовать их обратно в массив Numpy с помощью метода .toarray().
|
1 2 3 |
# создадим матрицу с преобладанием нулевых значений A = np.array([[2, 0, 0, 1, 0, 0, 0], [0, 0, 3, 0, 0, 2, 0], [0, 0, 0, 1, 0, 0, 0]]) A |
|
1 2 3 |
array([[2, 0, 0, 1, 0, 0, 0], [0, 0, 3, 0, 0, 2, 0], [0, 0, 0, 1, 0, 0, 0]]) |
Долю нулевых значений несложно посчитать через функцию np.count_nonzero() и атрибут size.
|
1 |
1.0 - np.count_nonzero(A) / A.size |
|
1 |
0.7619047619047619 |
Преобразуем матрицу в формат csr.
|
1 2 3 4 5 6 |
# импортируем функцию csr_matrix() from scipy.sparse import csr_matrix # и применим ее к матрице А B = csr_matrix(A) print(B) |
|
1 2 3 4 5 |
(0, 0) 2 (0, 3) 1 (1, 2) 3 (1, 5) 2 (2, 3) 1 |
Вернем матрицу csr обратно в формат массива Numpy.
|
1 2 |
C = B.toarray() C |
|
1 2 3 |
array([[2, 0, 0, 1, 0, 0, 0], [0, 0, 3, 0, 0, 2, 0], [0, 0, 0, 1, 0, 0, 0]], dtype=int64) |
Напомню, что с форматом csr мы впервые познакомились, когда изучали рекомендательные системы. Метод .toarray() мы активно применяли на занятии по обработке естественного языка.
Индексы и срезы
Индекс элемента массива
Подобно спискам, к элементам массива можно получить доступ по их индексу. Главное отличие — необходимо учитывать наличие измерений. Вначале рассмотрим индексы массива на схеме.
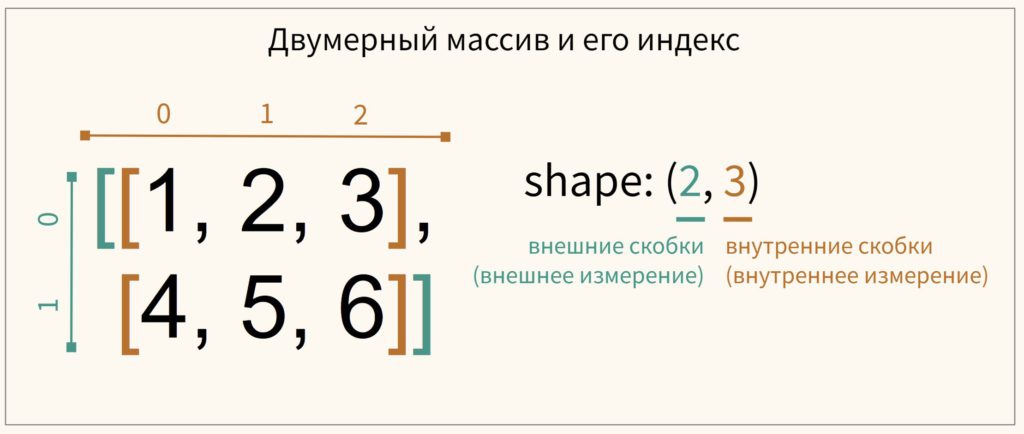
Если мы хотим получить доступ к элементу массива, то необходимо вначале указать индекс внешнего измерения (оно будет первым по счету в выводе атрибута shape), а затем индекс внутреннего.
Другими словами, мы двигаемся как бы снаружи вовнутрь, перемещаясь из одного измерения в другое.
Посмотрим, как это реализовать на Питоне. Создадим двумерный массив.
|
1 2 |
a = np.array([[1, 2, 3], [4, 5, 6]]) a |
|
1 2 |
array([[1, 2, 3], [4, 5, 6]]) |
Посмотрим на измерения и количество элементов в каждом из них.
|
1 |
a.shape |
|
1 |
(2, 3) |
Выведем первый элемент первого (внешнего) измерения.
|
1 2 |
# первый элемент представляет собой вектор a[0] |
|
1 |
array([1, 2, 3]) |
Второй индекс позволяет обратиться, например, к первому элементу первого вектора.
|
1 |
a[0][0] |
|
1 |
1 |
Теперь выведем значение шесть.
|
1 |
a[1][2] |
|
1 |
6 |
Срез массива
В массиве Numpy доступны и срезы (slice). Срез одномерного массива очень похож на срез списка.
|
1 2 3 |
# создадим одномерный массив b = np.array([1, 2, 3, 4, 5, 6, 7, 8]) b |
|
1 |
array([1, 2, 3, 4, 5, 6, 7, 8]) |
Возьмем каждый второй элемент в интервале с 1-го по 6-й индекс.
|
1 |
b[1:6:2] |
|
1 |
array([2, 4, 6]) |
Посмотрим на схему.

Когда измерений больше одного, внутри квадратных скобок измерения отделяются запятой. Создадим двумерный массив.
|
1 2 |
c = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) c |
|
1 2 |
array([[1, 2, 3, 4], [5, 6, 7, 8]]) |
Сделаем срез из первой строки (внешнее измерение) и первых двух столбцов (внутреннее измерение).
|
1 2 |
# 0 указывает на первую строку, диапазон :2 - на первые два столбца c[0, :2] |
|
1 |
array([1, 2]) |
Если нужно взять все элементы одного из измерений, достаточно поставить двоеточие без указания индекса.
|
1 2 |
# возьмем обе строки во втором столбце c[:, 1] |
|
1 |
array([2, 6]) |
С помощью среза можно вывести конкретный элемент массива.
|
1 2 |
# выведем элемент в первой строке и первом столбце c[0, 0] |
|
1 |
1 |
Другими словами, c[0, 0] == c [0][0].
Кроме того, обратите внимание, что индекс в формате array[i, j] и координаты элементов массива, которые мы рассмотрели ранее, это одно и то же.
Допускаются срезы с отрицательным индексом.
|
1 2 |
# выведем элемент в последней строке и последнем столбце c[-1, -1] |
|
1 |
6 |
Рассмотрим более сложный пример. Возьмем всю вторую строку [1] и каждый второй столбец [::2].
|
1 |
c[1, ::2] |
|
1 |
array([5, 7]) |
Теперь создадим массив с тремя измерениями.
|
1 2 3 |
# -1 означает, что Питон сам рассчитает количество элементов в этом измерении d = np.arange(16).reshape(4, 2, -1) d |
|
1 2 3 4 5 6 7 8 9 10 11 |
array([[[ 0, 1], [ 2, 3]], [[ 4, 5], [ 6, 7]], [[ 8, 9], [10, 11]], [[12, 13], [14, 15]]]) |
Можно сказать, что наш 3D массив состоит из четырех матриц 2 x 2.
Вначале выведем значение десять. Если идти снаружи вовнутрь, получается, что это третья матрица [2], второй вектор [1] и первый элемент [0].
|
1 |
d[2][1][0] |
|
1 |
10 |
Для срезов понадобится две запятых.
|
1 2 3 |
# выведем третью и четвертую матрицу [2:] # и в них вторую строку [1] и все столбцы [:] d[2:, 1, :] |
|
1 2 |
array([[10, 11], [14, 15]]) |
Если указать только один срез, мы будем работать только во внешнем измерении (с четырьмя матрицами).
|
1 2 |
# выведем первые две матрицы массива d[:2] |
|
1 2 3 4 5 |
array([[[0, 1], [2, 3]], [[4, 5], [6, 7]]]) |
Прежде чем завершить разговор про срезы, выведем первые строки каждой матрицы.
|
1 |
d[:, 0 , :] |
|
1 2 3 4 |
array([[ 0, 1], [ 4, 5], [ 8, 9], [12, 13]]) |
Оси массива
С концепцией измерения массива тесно связано понятие оси (axis, множественное число — axes). У массива столько же осей, сколько и измерений. Мы уже столкнулись с осями двух и трехмерного массивов, когда работали с изображениями.
Рассмотрим этот вопрос ещё раз.
Массив 2D
В двумерном массиве два измерения и соответственно две оси.
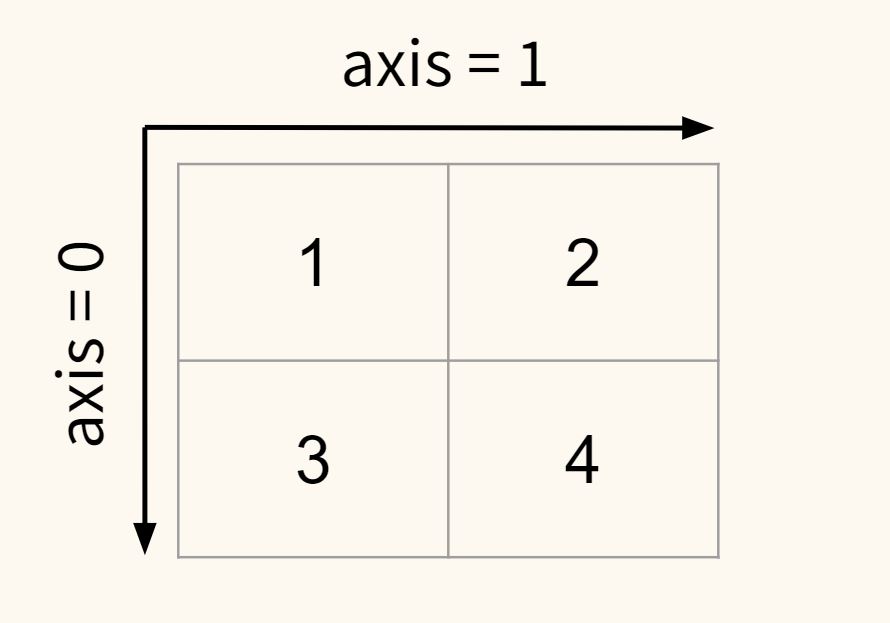
В документации Numpy существует такое понятие как первая и последняя ось. Применительно к двумерному массиву, ось 0 — это первая ось, а ось 1 — последняя.
Многие, в частности, математические и статистические методы в Numpy предполагают указание параметра оси. Продолжим работу с приведенным выше двумерным массивом.
|
1 2 |
arr_2D = np.array([[1, 2], [3, 4]]) arr_2D |
|
1 2 |
array([[1, 2], [3, 4]]) |
Сложение вдоль первой оси (axis = 0)
Найдем сумму по столбцам (вдоль оси 0).
|
1 |
np.sum(arr_2D, axis = 0) |
|
1 |
array([4, 6]) |

Сложение вдоль второй оси (axis = 1)
Теперь найдем сумму по строкам (вдоль оси 1).
|
1 |
np.sum(arr_2D, axis = 1) |
|
1 |
array([3, 7]) |

Обратите внимание, хотя axis = 0 принято ассоциировать со строками двумерного массива, сложение происходит вдоль вертикальной оси или по столбцам. Параметр axis = 1, отвечающий за столбцы, наоборот предполагает сложение вдоль горизонтальной оси по строкам.
При таких операциях говорят, что мы агрегируем (aggregate) данные и сворачиваем (collapse) или сокращаем (reduce) измерения вдоль определенной оси. И действительно, в каждой из описанных выше операций двумерный массив превратился в одномерный.
Сложение вдоль обеих осей (axis = (0, 1))
Если в параметр axis передать кортеж с указанием обеих осей (0, 1), сумма будет рассчитана сначала вдоль оси 0, затем вдоль оси 1.
|
1 |
np.sum(arr_2D, axis = (0, 1)) |
|
1 |
10 |

Если параметр axis не указывать, сумма также будет рассчитана по всем элементам массива.
|
1 |
np.sum(arr_2D) |
|
1 |
10 |
В этом случае «под капотом» стоит значение по умолчанию axis = None.
|
1 |
np.sum(arr_2D, axis = None) |
|
1 |
10 |
Отрицательные значения в параметре axis
Массив Numpy допускает отрицательное значение параметра axis. Параметр axis = −1 соответствует последней по счету оси, то есть оси 1.
|
1 |
np.sum(arr_2D, axis = -1) |
|
1 |
array([3, 7]) |
Сложение вдоль оси 0 соответствует параметру axis = −2.
|
1 |
np.sum(arr_2D, axis = -2) |
|
1 |
array([4, 6]) |
Массив 3D
Расположение осей трехмерного массива не всегда бывает очевидным.
Как уже было сказано, оси тесно связаны с измерениями и понять какая ось первая, какая вторая, а какая третья проще всего через атрибут shape. Вновь рассмотрим приведенный выше трехмерный массив.

Как мы видим, первая ось (axis = 0) в параметре shape всегда стоит на первом месте.
Сложение вдоль первой оси (axis = 0)
Применим функцию np.sum() с параметром axis = 0.
|
1 |
np.sum(arr_3D, axis = 0) |
|
1 2 |
array([[ 6, 8, 10], [12, 14, 16]]) |
Визуально это можно представить как поэлементное сложение двух матриц.
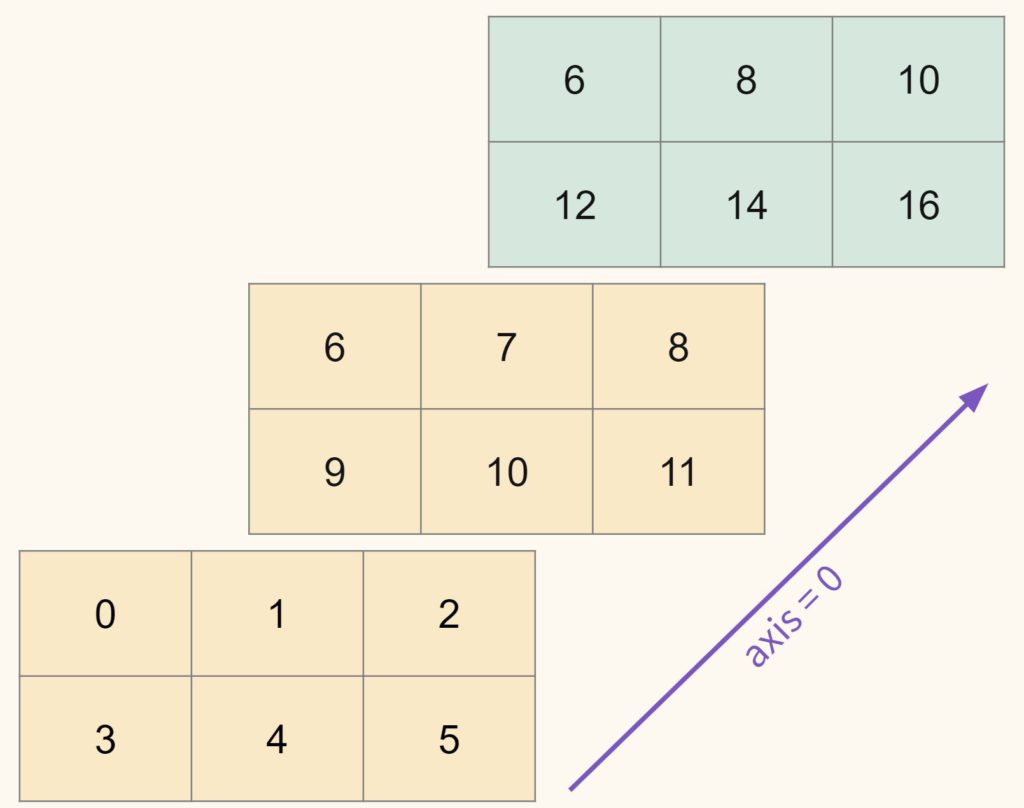
Если использовать индексы массива, то поэлементное сложение вдоль оси 0 можно реализовать следующим образом.
|
1 2 |
# возьмем первую матрицу arr_3D[0] |
|
1 2 |
array([[0, 1, 2], [3, 4, 5]]) |
|
1 2 |
# возьмем вторую матрицу arr_3D[1] |
|
1 2 |
array([[ 6, 7, 8], [ 9, 10, 11]]) |
|
1 2 |
# и поэлементно сложим их arr_3D[0] + arr_3D[1] |
|
1 2 |
array([[ 6, 8, 10], [12, 14, 16]]) |
Эту же задачу можно решить с помощью цикла for. Вначале нам нужно создать нулевую матрицу, размерность которой будет соответствовать желаемому результату сложения вдоль оси 0.
|
1 2 |
# создадим нулевую матрицу размером 2 x 3 total = np.zeros((2, 3)) |
Теперь создадим цикл for с двумя итерациями (потому что мы складываем две матрицы внутри трехмерного массива) через функцию range() с параметром 2.
|
1 2 |
for i in range(2): total += arr_3D[i] |
Внутри цикла мы на первой итерации (i равно 0) запишем в нулевой массив нашу первую матрицу, а на второй итерации (i равно 1) поэлементно прибавим вторую. Переменная i в данном случае стала индексом для массива arr_3D.
|
1 |
total |
|
1 2 |
array([[ 6., 8., 10.], [12., 14., 16.]]) |
Мы применили цикл for к массиву Numpy исключительно в учебных целях. На практике этого стоит избегать. Встроенные функции Numpy исполняются гораздо быстрее.
Сложение вдоль второй оси (axis = 1)
Теперь посмотрим на сложение с параметром axis = 1.
|
1 2 |
# применим np.sum() np.sum(arr_3D, axis = 1) |
|
1 2 |
array([[ 3, 5, 7], [15, 17, 19]]) |
Сложение вдоль оси 1 предполагает, что мы складываем столбцы каждой матрицы.

Посмотрим на сложение через индексы.
|
1 2 |
# сложим столбцы первой arr_3D[0][0] + arr_3D[0][1] |
|
1 |
array([3, 5, 7]) |
|
1 2 |
# и второй матрицы arr_3D[1][0] + arr_3D[1][1] |
|
1 |
array([15, 17, 19]) |
Теперь, опять же в учебных целях, решим эту задачу через цикл for.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# создадим нулевую матрицу 2 x 3 total = np.zeros((2, 3)) # вначале пройдемся по матрицам for i in range(2): # затем по строкам каждой матрицы for j in range(2): # и в первую строку total запишем сумму столбцов первой матрицы arr_3D, # а во вторую - сумму столбцов второй матрицы total[i] += arr_3D[i][j] total |
|
1 2 |
array([[ 3., 5., 7.], [15., 17., 19.]]) |
Сложение вдоль третьей оси (axis = 2)
|
1 2 |
# применим np.sum() np.sum(arr_3D, axis = 2) |
|
1 2 |
array([[ 3, 12], [21, 30]]) |
Сложение вдоль оси 2 предполагает, что мы складываем строки каждой матрицы.
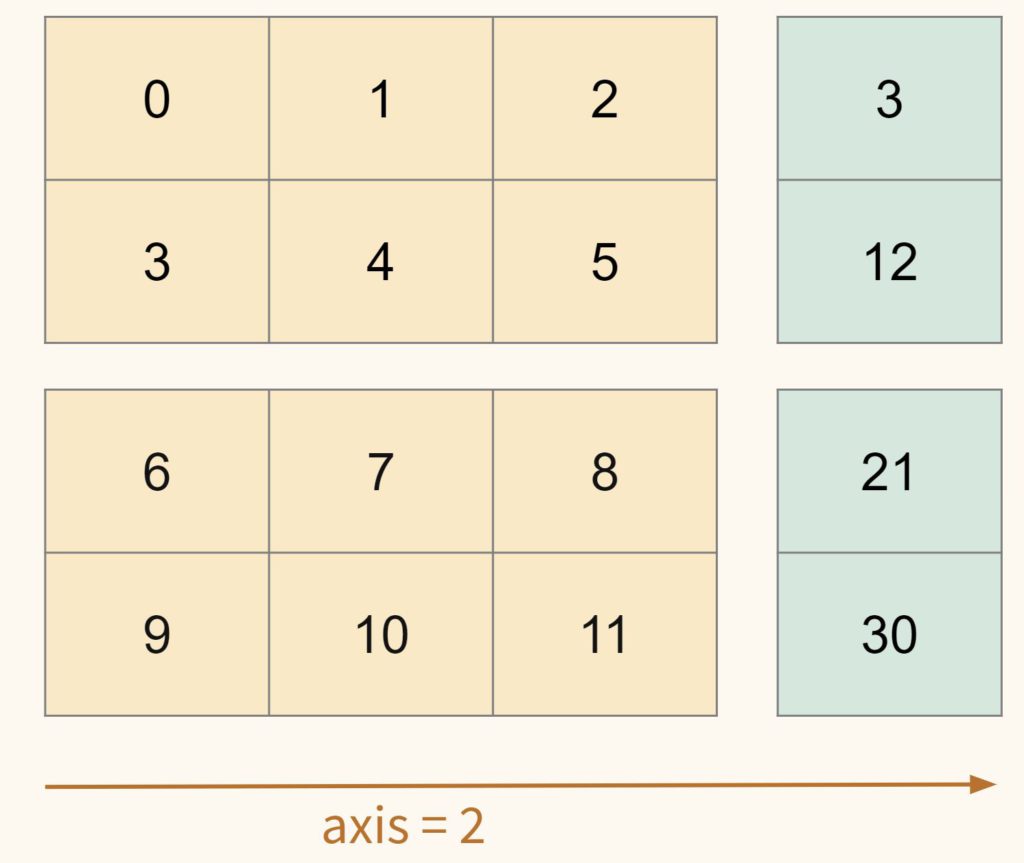
Покажем сложение строк через индексы для первой строки первой матрицы [0, 1, 2].
|
1 |
arr_3D[0][0][0] + arr_3D[0][0][1] + arr_3D[0][0][2] |
|
1 |
3 |
Сложение каждой строки можно посмотреть в ноутбуке⧉. Теперь применим цикл for.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# создадим нулевой массив 2 x 2 для записи результатов total = np.zeros((2, 2)) # пройдемся по матрицам for i in range(2): # по строкам матрицы for j in range(2): # и по столбцам for k in arr_3D[i][j]: # индексы i, j запишут результат сложения элементов строк k # в квадратную матрицу 2 x 2 total[i][j] += k total |
|
1 2 |
array([[ 3., 12.], [21., 30.]]) |
Сложение вдоль первой и второй осей (axis = (0, 1))
|
1 2 |
# применим функцию np.sum() np.sum(arr_3D, axis = (0, 1)) |
|
1 |
array([18, 22, 26]) |
Здесь мы объединили две операции сложения вначале вдоль оси 0, затем вдоль оси 1. Схемы этих операций можно посмотреть выше.
В цикле for этот алгоритм можно реализовать либо (1) через два отдельных цикла, либо (2) через вложенные друг в друга циклы. При использовании двух циклов (1) мы вначале складываем матрицы.
|
1 2 3 4 5 6 7 |
# произведем сложение по оси 0 total_0 = np.zeros((2, 3)) for i in range(2): total_0 += arr_3D[i] total_0 |
|
1 2 |
array([[ 6., 8., 10.], [12., 14., 16.]]) |
На втором этапе мы складываем столбцы предыдущего результата.
|
1 2 3 4 5 6 7 |
# произведем сложение по оси 1 total_1 = np.zeros(3) for j in range(2): total_1 += total_0[j] total_1 |
|
1 |
array([18., 22., 26.]) |
При использовании вложенных циклов (2) мы пройдемся по строкам каждой матрицы и поэлементно сложим их (т.е. произведем сложение по столбцам).
|
1 2 3 4 5 6 7 |
total = np.zeros(3) for i in range(2): for j in range(2): total += arr_3D[i][j] total |
|
1 |
array([18., 22., 26.]) |
Сложение вдоль всех трех осей (axis = (0, 1, 2))
При сложении вдоль всех трех осей мы можем указать каждую ось в параметре axis.
|
1 |
np.sum(arr_3D, axis = (0, 1, 2)) |
|
1 |
66 |
Кроме того, аналогично двумерному массиву, если параметр axis не указывать, сложение также будет произведено по всем измерениям.
|
1 |
np.sum(arr_3D) |
|
1 |
66 |
Реализация алгоритма через цикл for в данном случае достаточно проста.
|
1 2 3 4 5 6 7 8 9 10 11 |
total = 0 # в трех вложенных циклах мы пройдемся по всем элементам массива for i in range(2): for j in range(2): for k in range(3): # и запишем сумму этих элементов в переменную total total += arr_3D[i][j][k] total |
|
1 |
66 |
В целом, результатом сложения по всем измерениям для массива любой размерности будет скаляр (число).
Обратите внимание, при работе с трехмерным массивом также происходит агрегирование данных и сокращение измерений. Исчезает та ось или измерение, вдоль которого осуществлялось сложение.
Напоследок замечу, что мы использовали функцию np.sum() в большей степени для иллюстриции операций вдоль определенной оси. Математические возможности Numpy будут рассмотрены на следующем занятии.
Операции с массивами
Функция len()
Вновь возьмем трехмерный массив.
|
1 2 |
arr_3D = np.arange(12).reshape(2, 2, 3) arr_3D |
|
1 2 3 4 5 |
array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]]]) |
По умолчанию функция len() выводит длину внешнего измерения (ось 0). Это внешние скобки, в которых содержатся две матрицы 2 x 3.
|
1 |
len(arr_3D) |
|
1 |
2 |
Для того чтобы вывести, например, длину внутреннего измерения, т.е. вектора из трех элементов (ось 1), нужно воспользоваться индексом.
|
1 |
len(arr_3D[0][0]) |
|
1 |
3 |
Вхождение элемента в массив
Проверим, входит ли значение 3 в созданный выше массив arr_3D.
|
1 |
3 in arr_3D |
|
1 |
True |
Теперь проверим, не входит ли значение 11.
|
1 |
11 not in arr_3D |
|
1 |
False |
Распаковка массива
Возьмем матрицу из трех строк и девяти столбцов.
|
1 2 |
a = np.arange(1, 28).reshape(3, 9) a |
|
1 2 3 |
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9], [10, 11, 12, 13, 14, 15, 16, 17, 18], [19, 20, 21, 22, 23, 24, 25, 26, 27]]) |
Во внешнем измерении (ось 0) три элемента. Мы можем распаковать (unpack) их в три переменные.
|
1 |
x, y, z = a |
Выведем первую переменную (строку).
|
1 |
x |
|
1 |
array([1, 2, 3, 4, 5, 6, 7, 8, 9]) |
Теперь распакуем первый, последний и остальные элементы первой строки в отдельные переменные.
|
1 |
x, *y, z = a[0] |
Выведем каждую переменную.
|
1 2 3 |
print(x) print(y) print(z) |
|
1 2 3 |
1 [2, 3, 4, 5, 6, 7, 8] 9 |
С таким способом распаковки мы познакомились, когда говорили про списки.
Изменение элементов массива
Обратимся к двумерному массиву.
|
1 2 |
arr_2D = np.array([[1, 2, 3], [4, 5, 6]]) arr_2D |
|
1 2 |
array([[1, 2, 3], [4, 5, 6]]) |
Заменим первый элемент первой строки по его индексу.
|
1 2 |
arr_2D[0, 0] = 2 arr_2D |
|
1 2 |
array([[2, 2, 3], [4, 5, 6]]) |
Запишем значение 1 в первую строку.
|
1 2 |
arr_2D[0] = 1 arr_2D |
|
1 2 |
array([[1, 1, 1], [4, 5, 6]]) |
Пусть третий столбец массива состоит из нулей.
|
1 2 |
arr_2D[:,2] = 0 arr_2D |
|
1 2 |
array([[1, 1, 0, 1], [5, 6, 0, 8]]) |
Теперь потренируемся с трехмерным массивом.
|
1 2 |
arr_3D = np.arange(12).reshape(2, 2, 3) arr_3D |
|
1 2 3 4 5 |
array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]]]) |
Выберем второй столбец второй матрицы и заменим значения столбца 7 и 10 на 0 и 1.
|
1 2 3 4 |
# при такой операции размер среза должен совпадать # с количеством передаваемых значений arr_3D[1, :, 1] = [0, 1] arr_3D |
|
1 2 3 4 5 |
array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 0, 8], [ 9, 1, 11]]]) |
Заменим все элементы массива на число семь с помощью метода .fill().
|
1 2 |
arr_3D.fill(7) arr_3D |
|
1 2 3 4 5 |
array([[[7, 7, 7], [7, 7, 7]], [[7, 7, 7], [7, 7, 7]]]) |
Сортировка массива и обратный порядок его элементов
Функция np.sort()
Возьмем двумерный массив.
|
1 2 |
a = np.array([[4, 8, 2], [2, 3, 1]]) a |
Как и во многих других функциях главное разобраться с применением параметра axis. По умолчанию сортировка идет с параметром axis = −1 (последняя ось).
|
1 |
np.sort(a) |
|
1 2 |
array([[2, 4, 8], [1, 2, 3]]) |
Для двумерного массива это ось 1.
|
1 |
np.sort(a, axis = 1) |
|
1 2 |
array([[2, 4, 8], [1, 2, 3]]) |
Теперь посмотрим на сортировку по оси 0.
|
1 |
np.sort(a, axis = 0) |
|
1 2 |
array([[2, 3, 1], [4, 8, 2]]) |
Параметр axis = None вначале возвращает одномерный массив, а затем сортирует его.
|
1 |
np.sort(a, axis = None) |
|
1 |
array([1, 2, 2, 3, 4, 8]) |
Обратный порядок элементов массива
Для того чтобы задать обратный порядок элементов, можно использовать оператор среза с параметром шага −1.
|
1 |
np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])[::-1] |
|
1 |
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0]) |
Обратный порядок элементов можно совмещать со срезами.
|
1 2 |
# обратите внимание, мы используем и положительный, и отрицательный индексы np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])[-3: 3: -1] |
|
1 |
array([7, 6, 5, 4]) |
Теперь возьмем двумерный массив.
|
1 2 |
a = np.array([[4, 8, 2], [2, 3, 1], [1, 7, 2]]) a |
|
1 2 3 |
array([[4, 8, 2], [2, 3, 1], [1, 7, 2]]) |
С помощью оператора среза можно задать обратный порядок по двум измерениям.
|
1 2 |
# такая запись аналогична параметру axis = (0, 1) a[::-1, ::-1] |
|
1 2 3 |
array([[2, 7, 1], [1, 3, 2], [2, 8, 4]]) |
Разумеется, мы можем задать обратный порядок только по внешнему или только внутреннему измерениям.
|
1 2 |
# обратный порядок по внешнему (axis = 0) a[::-1] |
|
1 2 3 |
array([[1, 7, 2], [2, 3, 1], [4, 8, 2]]) |
|
1 2 |
# и внутреннему измерению (axis = 1) a[:, ::-1] |
|
1 2 3 |
array([[2, 8, 4], [1, 3, 2], [2, 7, 1]]) |
Помимо этого, обратный порядок можно задать через функцию np.flip(). По умолчанию эта функцию задает обратный порядок по двум измерениям.
|
1 2 |
# то же самое, что axis = (0, 1) np.flip(a) |
|
1 2 3 |
array([[2, 7, 1], [1, 3, 2], [2, 8, 4]]) |
Отдельно можно задать порядок по внешнему и внутреннему измерениям.
|
1 2 |
# внешнее измерение np.flip(a, axis = 0) |
|
1 2 3 |
array([[1, 7, 2], [2, 3, 1], [4, 8, 2]]) |
|
1 2 |
# внутреннее измерение np.flip(a, axis = 1) |
|
1 2 3 |
array([[2, 8, 4], [1, 3, 2], [2, 7, 1]]) |
Сортировка в убывающем порядке
Возможно вы обратили внимание, что при использовании функции np.sort() мы сортировали элементы только в возрастающем порядке. По другому она не умеет. Для того чтобы отсортировать элементы в убывающем порядке можно воспользоваться оператором среза.
|
1 2 |
# возьмем простой одномерный массив a = np.array([4, 2, 6, 1, 7, 3, 5]) |
Одновременно применим функцию np.sort() и оператор среза с параметром шага −1.
|
1 |
np.sort(a)[::-1] |
|
1 |
array([7, 6, 5, 4, 3, 2, 1]) |
Обращу ваше внимание, что исходный массив не изменился.
|
1 |
a |
|
1 |
array([4, 2, 6, 1, 7, 3, 5]) |
При этом можно воспользоваться и методом .sort().
|
1 2 |
# здесь нужно сначала задать обратный порядок, а потом отсортировать a[::-1].sort() |
|
1 |
array([7, 6, 5, 4, 3, 2, 1]) |
Изменится исходный массив.
|
1 |
a |
|
1 |
array([7, 6, 5, 4, 3, 2, 1]) |
Изменение размерности
Метод .reshape()
Возьмем простой трехмерный массив.
|
1 2 |
arr_3D = np.arange(12).reshape(2, 2, 3) arr_3D |
|
1 2 3 4 5 |
array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]]]) |
|
1 2 |
# в нем 12 элементов arr_3D.size |
|
1 |
12 |
С помощью метода .reshape() мы можем изменить количество измерений. Например, мы можем превратить этот массив в матрицу с размерностью 2 x 6.
|
1 2 3 |
# при этом важно, чтобы общее количество элементов было тем же arr_2D = arr_3D.reshape(2, 6) arr_2D |
|
1 2 |
array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11]]) |
Функция np.resize() и метод .resize()
С другой стороны, если мы хотим не только задать другую размерность, но и изменить общее количество элементов, то мы можем воспользоваться функцией np.resize() и методом .resize().
|
1 2 3 |
# функция np.resize() позволяет не сохранять прежнее количество элементов # существующие элементы копируются в новые ячейки np.resize(arr_2D, (3, 6)) |
|
1 2 3 |
array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [ 0, 1, 2, 3, 4, 5]]) |
Перед тем как воспользоваться методом .resize() нам необходимо создать копию массива arr_2D. Все дело в том, что переменная arr_2D ссылается на другой массив (в частности, на трехмерный массив arr_3D), а метод .resize() может работать только с исходным массивом.
|
1 |
arr_2D_copy = arr_2D.copy() |
Метод .resize() также создаст отдельную копию, изменит размерность и заполнит пропуски нулями.
|
1 2 |
arr_2D_copy.resize(4, 6) arr_2D_copy |
|
1 2 3 4 |
array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [ 0, 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0, 0]]) |
Методы .flatten() и .ravel()
Метод .flatten() переводит («вытягивает») массив в одно измерение и создает копию исходного массива (как метод .copy()).
|
1 |
arr_3D.flatten() |
|
1 |
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) |
Напомню, что концепцию вытягивания массива мы использовали при работе с изображениями на занятиях по компьютерному зрению и основам нейронных сетей.
Метод .ravel() делает то же самое, но не создает копию исходного массива и за счет этого быстрее, чем .flatten().
|
1 |
arr_3D.ravel() |
|
1 |
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) |
Метод .ravel() мы использовали на занятии по обработке естественного языка.
np.newaxis
Объект np.newaxis добавляет измерение в уже существующем массиве.
|
1 2 3 |
# создадим одномерный массив a = np.array([1, 2, 3]) a.shape |
|
1 |
(3,) |
Мы можем добавить в этот массив новое первое измерение и, таким образом, сделать существующее измерение вторым.
|
1 2 3 4 |
b = a[np.newaxis, :] print(b) print(b.shape) |
|
1 2 |
[[1 2 3]] (1, 3) |
Аналогично, мы можем добавить новое второе измерение, а существующее измерение оставить первым.
|
1 2 3 4 |
c = a[:, np.newaxis] print(c) print(c.shape) |
|
1 2 3 4 |
[[1] [2] [3]] (3, 1) |
Функция np.expand_dims()
Функция np.expand_dims() добавляет измерение, указанное в параметре axis. Возьмем двумерный массив.
|
1 2 |
a = np.array([[1,2], [3,4]]) a |
|
1 2 |
array([[1, 2], [3, 4]]) |
Добавим внешнее измерение.
|
1 |
np.expand_dims(x, axis = 0) |
|
1 2 |
array([[[1, 2], [3, 4]]]) |
Теперь добавим измерение «по середине».
|
1 |
np.expand_dims(x, axis = 1) |
|
1 2 3 |
array([[[1, 2]], [[3, 4]]]) |
А также внутреннее измерение.
|
1 |
np.expand_dims(x, axis = 2) |
|
1 2 3 4 5 |
array([[[1], [2]], [[3], [4]]]) |
Функция np.squeeze()
Возьмем массив 4D, в котором первое и последнее измерения содержат по одному элементу.
|
1 2 |
arr_4D = np.arange(9).reshape(1, 3, 3, 1) arr_4D |
|
1 2 3 4 5 6 7 8 9 10 11 |
array([[[[0], [1], [2]], [[3], [4], [5]], [[6], [7], [8]]]]) |
Удалим эти измерения с помощью функции np.squeeze().
|
1 |
np.squeeze(arr_4D) |
|
1 2 3 |
array([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) |
Новый массив имеет только два измерения.
|
1 |
np.squeeze(arr_4D).shape |
|
1 |
(3, 3) |
Этот метод мы использовали при создании рекомендательной системы.
Объединение массивов
Функция np.concatenate()
Предположим, что у нас есть два квардратных массива a и b размерностью 2 x 2.
|
1 2 |
a = np.arange(4).reshape(2, 2) a |
|
1 2 |
array([[0, 1], [2, 3]]) |
|
1 2 |
b = np.arange(4, 8).reshape(2, 2) b |
|
1 2 |
array([[4, 5], [6, 7]]) |
Объединим массивы вдоль оси 0 без добавления нового измерения.
|
1 |
np.concatenate((a, b), axis = 0) |
|
1 2 3 4 |
array([[0, 1], [2, 3], [4, 5], [6, 7]]) |
Точно так же массивы можно объединить вдоль оси 1.
|
1 |
np.concatenate((a, b), axis = 1) |
|
1 2 |
array([[0, 1, 4, 5], [2, 3, 6, 7]]) |
Функция np.stack()
Отличие функции np.stack() от np.concatenate() в том, что при объединении массивов мы добавляем новое измерение (новую ось).
|
1 2 |
# при axis = 0 мы просто добавляем внешнее измерение np.stack((a, b), axis = 0) |
|
1 2 3 4 5 |
array([[[0, 1], [2, 3]], [[4, 5], [6, 7]]]) |
Несколько более сложным оказывается поведение при axis = 1 и axis = 2.
|
1 2 |
# при axis = 1 мы объединяем первые и вторые строки двух массивов np.stack((a, b), axis = 1) |
|
1 2 3 4 5 |
array([[[0, 1], [4, 5]], [[2, 3], [6, 7]]]) |
|
1 2 |
# при axis = 2 объединяются элементы с одинаковыми индексами np.stack((a, b), axis = 2) |
|
1 2 3 4 5 |
array([[[0, 4], [1, 5]], [[2, 6], [3, 7]]]) |
Фильтр (маска) массива
Задача фильтрации массива (или как еще говорят создания маски массива) встречается довольно часто. К примеру, предположим, что мы собрали показания прибора, однако из-за ошибки датчика часть из них оказалась некорректной, и для последующего анализа эти значения нужно удалить.
Логическая маска (Boolean mask)
Пусть дан массив Numpy, и мы хотим удалить из него отрицательные значения.
|
1 |
a = np.array([5, 7, -3, 4, 2, -4]) |
Для того чтобы создать фильтр массива достаточно указать критерий отбора. На выходе мы получим массив из логических значений True и False, в котором нежелательные значения будут помечены как False.
|
1 |
a > 0 |
|
1 |
array([ True, True, False, True, True, False]) |
Применим маску к исходному массиву.
|
1 2 |
# останутся только те значения, которые в маске помечены как True a[a > 0] |
|
1 |
array([5, 7, 4, 2]) |
Кроме того, отфильтрованные значения можно заполнить, например, нулями.
|
1 2 |
a[a < 0] = 0 a |
|
1 |
array([5, 7, 0, 4, 2, 0]) |
Отдельно отмечу, что удаление или заполнение нулями некачественно собранных данных далеко не всегда является оптимальной стратегией. Более подробно мы поговорим об этом на курсе анализа и обработки данных.
Пороговое преобразование изображения
Еще одним примером использования фильтра массива является так называемое пороговое преобразование. Его мы изучали на занятии по компьютерному зрению. Рассмотрим этот код еще раз.
|
1 2 3 4 5 |
# импортируем фотографии из библиотеки skimage from skimage import data # загрузим изображение с оттенками серого camera = data.camera() |
Каждый пиксель изображения с оттенками серого (grayscale image), напомню, представляет собой значение в диапазоне от 0 до 255. Мы можем задать некоторый порог, пусть это будет число 87, и все значения выше этого порога сделать True или единицей, а ниже — False или нулем. Далее, если преобразовать единицы и нули в белый и черный цвета соответственно, то на выходе мы получим черно-белое изображение (binary image), в котором передний и задний планы разделены.
Подобный массив из значений False и True есть не что иное как маска исходного массива.
|
1 2 |
# создадим маску binary = camera > 87 |
Посмотрим на значения исходного массива.
|
1 2 |
# для наглядности возьмем небольшой срез из середины массива camera[150, 65:75] |
|
1 |
array([220, 219, 219, 196, 80, 54, 47, 45, 44, 44], dtype=uint8) |
И на значения его маски.
|
1 |
binary[150, 65:75] |
|
1 2 |
array([ True, True, True, True, False, False, False, False, False, False]) |
Остается визуально оценить результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# сравним исходное изображение и изображение после преобразования fig, ax = plt.subplots(1, 2, figsize = (8, 4)) # выведем первое изображение и зададим заголовок ax[0].imshow(camera, cmap = 'gray') ax[0].set_title('До') # для ч/б изображений не забудем про параметр cmap = 'gray' ax[1].imshow(binary, cmap = 'gray') ax[1].set_title('После') plt.show() |

Masked array
Альтернативный способ фильтрации массива Numpy предполагает использование модуля ma (masked array).
|
1 2 3 4 5 |
# импортируем модуль ma import numpy.ma as ma # вновь воспользуемся массивом с отрицательными числами a = np.array([5, 7, -3, 4, 2, -4]) |
В отличие от описанного выше логического фильтра, в masked array опускаются элементы, помеченные как 1 или True.
|
1 2 |
# функции masked_array мы передаем сам массив и его маску с 0 или 1 ma.masked_array(a, mask = [0, 0, 1, 0, 0, 1]) |
|
1 2 3 |
masked_array(data=[5, 7, --, 4, 2, --], mask=[False, False, True, False, False, True], fill_value=999999) |
|
1 2 |
# можно также передать значения False или True ma.masked_array(a, mask = [False, False, True, False, False, True]) |
|
1 2 3 |
masked_array(data=[5, 7, --, 4, 2, --], mask=[False, False, True, False, False, True], fill_value=999999) |
Обратите внимание, нежелательные значения не исчезают полностью, а заполняются --.
Кроме того, для некоторых логических условий есть отдельные функции. Например, мы можем опустить все элементы меньше определенного значения.
|
1 2 |
# в данном случае меньше 0 ma.masked_less(a, 0) |
|
1 2 3 |
masked_array(data=[5, 7, --, 4, 2, --], mask=[False, False, True, False, False, True], fill_value=999999) |
Рассмотрим еще одну возможность модуля ma. Возьмем массив, в котором есть пропущенные значения (NaN, Not a Number) и значение бесконечности (inf, infinity).
|
1 |
b = np.array([5, 7, np.nan, 4, 2, np.inf]) |
Если мы попробуем посчитать сумму этих значений, результатом будет пропущенное значение.
|
1 |
b.sum() |
|
1 |
nan |
Для решения этой проблемы мы можем применить функцию masked_invalid(). Она автоматически отфильтровывает пропущенные значения и значения бесконечности.
|
1 2 |
b_masked = ma.masked_invalid(b) b_masked |
|
1 2 3 |
masked_array(data=[5.0, 7.0, --, 4.0, 2.0, --], mask=[False, False, True, False, False, True], fill_value=1e+20) |
Теперь мы можем без труда сложить оставшиеся элементы.
|
1 |
b_masked.sum() |
|
1 |
18.0 |
Более того, с помощью метода .filled() мы можем заполнить образовавшиеся пропуски. Например, средним арифметическим оставшихся элементов.
|
1 2 3 |
# использование среднего значения часто является более предпочтительным # способом заполнения пропусков b_masked.filled(b_masked.mean()) |
|
1 |
array([5. , 7. , 4.5, 4. , 2. , 4.5]) |
Прежде чем завершить, рассмотрим еще одну дополнительную тему, а именно вызов справки непосредственно в Google Colab.
Документация
Справку по функции можно вызвать с помощью знака вопроса. Документация появится в отдельном окне.
|
1 2 |
# знак вопроса может стоять перед ?print |
|
1 2 |
# или после вызываемой функции print? |
Обратите внимание, мы не использовали круглых скобок.
Кроме того, можно применить функцию help(). В этом случае документация появится под вызываемой функцией.
|
1 |
help(print) |
|
1 2 3 4 5 6 7 8 9 10 11 |
Help on built-in function print in module builtins: print(...) print(value, ..., sep=' ', end='\n', file=sys.stdout, flush=False) Prints the values to a stream, or to sys.stdout by default. Optional keyword arguments: file: a file-like object (stream); defaults to the current sys.stdout. sep: string inserted between values, default a space. end: string appended after the last value, default a newline. flush: whether to forcibly flush the stream. |
С помощью функции np.lookfor() мы можем осуществить поиск непосредственно по документации Numpy.
|
1 2 3 |
# поиск будет выполнен по передаваемому ключевому слову, # а результаты отсортированы по важности np.lookfor('randint') |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Search results for 'randint' ---------------------------- numpy.random.RandomState.randint Return random integers from `low` (inclusive) to `high` (exclusive). numpy.chararray.item a.item(*args) numpy.chararray.itemset a.itemset(*args) numpy.random.tests.test_random.TestRandint.rfunc Return random integers from `low` (inclusive) to `high` (exclusive). numpy.random.Generator.integers Return random integers from `low` (inclusive) to `high` (exclusive), or numpy.random.RandomState.choice Generates a random sample from a given 1-D array ... |
Подведем итог
На сегодняшнем занятии мы достаточно подробно рассмотрели массив Numpy. В частности, мы узнали о том, как создавать массив, какие у него есть атрибуты и как реализована многомерность массива. Мы изучили индексы и оси, а также поговорили про основные операции с массивами.
Вопросы для закрепления
Вопрос. Как выяснить очередность осей массива?
Посмотреть правильный ответ
Ответ: атрибут shape на первое место ставит элементы внешнего измерения (внешних скобок), на последнее — внутренних. Внешнее измерение — это первая ось (axis = 0), внутренее — последняя (axis = −1).
Вопрос. Что происходит с осью (измерением), вдоль которой происходит сложение элементов массива?
Посмотреть правильный ответ
Ответ: это измерение исчезает (и соответственно перестает фигурировать в атрибуте shape) за счет агрегирования его элементов.
Вопрос. Как отсортировать массив в убывающем порядке?
Посмотреть правильный ответ
Ответ: применить функцию np.sort() или метод .sort() вместе с оператором среза с отрицательным шагом.
В ноутбуке к лекции приведены дополнительные упражнения⧉.
На следующем занятии мы сделаем акцент на математических и статистических возможностях библиотеки Numpy.