Модуль random. Часть 2 | Программирование на Питоне

Все курсы > Программирование на Питоне > Занятие 10 (часть 2)

Во второй части перейдем к изучению вероятностному распределению дискретных случайных величин.

Содержание занятия

Дискретные и непрерывные случайные величины

Случайные величины делятся на дискретные и непрерывные.

Дискретная случайная величина

Дискретная случайная величина — это случайная величина, значения которой конечны и счетны.

Помимо бросания игральной кости, классическими примерами дискретной случайной величины являются подбрасывания монеты или раздача колоды карт. Более жизненный пример — количество автомобилей, проезжающих по улице города за сутки.

На числовой прямой такая величина может быть отмечана только на определенных точках.

Непрерывная случайная величина

Непрерывная случайная величина может быть получена в результате измерений (например, рост человека, температура воздуха, время ожидания в очереди и так далее).

На числовой прямой такая величина может принимать любое значение в пределах заданного интервала.

Вероятностное распределение

А теперь давайте попробуем провести множество подсчётов (для дискретной) и измерений (для непрерывной) случайной величины и вывести их на одном графике. Начнем с дискретных величин.

Дискретное вероятностное распределение

Мы снова будем бросать игральную кость, но на этот раз существенно увеличим количество испытаний.

# зададим точку отсчета

np.random.seed(42)

# бросим кость 100 000 раз

dice = np.random.randint(1, 7, 100000)

# выведем первые 10 результатов

dice[:10]

1	array([4, 5, 3, 5, 5, 2, 3, 3, 3, 5])

С помощью функции np.unique() посчитаем, сколько раз выпадет каждый из шести возможных исходов.

# функция np.unique() возвращает перечень уникальных элементов массива

# и их количество при параметре return_counts = True

elements, counts = np.unique(dice, return_counts = True)

print(elements)

print(counts)

1 2	[1 2 3 4 5 6] [16592 16799 16390 16776 16810 16633]

Теперь рассчитаем долю каждого исхода в общем количестве испытаний.

# выполним поэлементное деление частоты каждого исхода на общее количество бросков

rel_freq = (counts / len(dice)).round(3)

rel_freq

1	array([0.166, 0.168, 0.164, 0.168, 0.168, 0.166])

Увидеть такое распределение можно с помощью столбчатой диаграммы.

# зададим размер графика

plt.figure(figsize = (7,5))

# передадим в plt.bar() категории (элементы) и их относительную частоту

# зададим параметр width, который контролирует ширину столбца

plt.bar(elements, rel_freq, width = 0.98)

plt.show()

Обратите внимание, с помощью графика мы можем оценить вероятность каждого из исходов. Именно для этого и нужно вероятностное распределение. Мы можем оценить случайный процесс в целом.

Равномерное дискретное распределение

Как вы видите, вероятность наступления каждого исхода примерно одинакова. Такое распределение называется равномерным (discrete uniform distribution). Именно его и использует функция np.random.randint() при генерации чисел.

Небольшие расхождения вероятностей каждого из шести исходов объясняются тем, что мы используем эмпирическую, а не теоретическую вероятность. Теоретически эти вероятности одинаковы.

Посмотрим на нотацию равномерного распределения

$$ X \sim U(a, b) $$

В данном случае a и b — минимальное и максимальное значения случайной величины X. При бросании кости a и b равны одному и шести соответственно.

$$ X \sim U(1, 6) $$

Функция вероятности

Помимо графика, дискретное вероятностное распределение удобно описывать с помощью функции вероятности (probability mass function, pmf). Такая функция возвращает вероятность того, что случайная величина примет определенное значение.

В случае равномерного распределения вероятность каждого исхода одинакова, а функция вероятности чрезвычайно проста.

$$ pmf = \frac {1}{n} $$

Параметр n можно рассчитать по формуле

$$ n = b-a+1 $$

Вероятность каждого исхода, таким образом, будет равна 1/6.

$$ pmf = \frac{1}{6-1+1} = \frac{1}{6} $$

Рассмотрим эту функцию на графике.

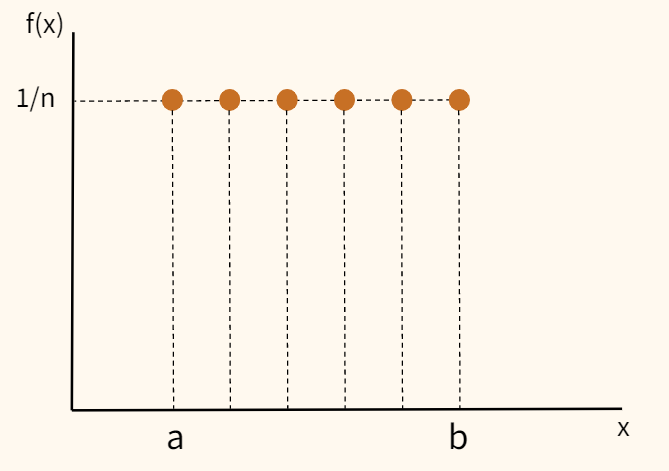
Функцию вероятности рассматриваемой нами дискретной величины также можно представить в форме таблицы.

Еще раз обращу ваше внимание на то, что сумма вероятностей любого распределения равна единице.

1	np.sum(rel_freq).round()

1.0

Функция распределения

Одновременно, вероятностное распределение бывает удобно описать с помощью (кумулятивной, накопительной) функции распределения (cumulative distribution function, cdf). Эта функция возвращает вероятность того, что случайная величина примет значение меньше заданного. Говоря неформально, она показывает «накопившуюся» вероятность исходов.

Для равномерного дискретного распределения функция распределения выглядит следующим образом

$$ cdf(k; a, b) = \frac{[k]-a+1}{b-a+1} $$

где k — это возможный исход в границах между а и b, то есть $k \in [a, b]$.

Приведем пример. При бросании кости рассчитаем вероятность выпадения тройки или меньшего значения (то есть 1, 2 или 3).

$$ cdf(3; 1, 6) = \frac{3-1+1}{6-1+1} = \frac{3}{6} = \frac{1}{2} $$

Посмотрим на эту вероятность на графике функции распределения.

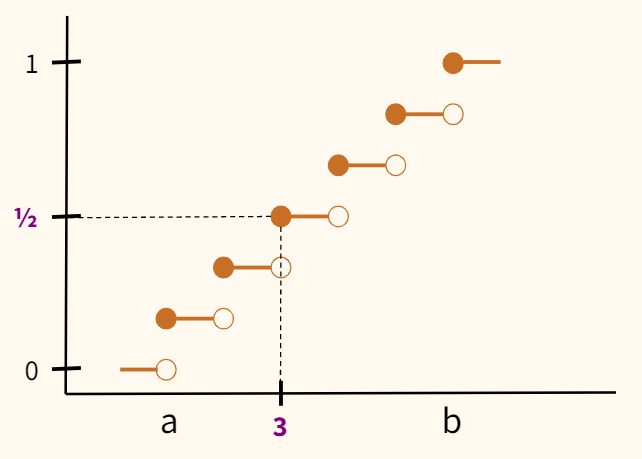
Математическое ожидание

Кроме того, вероятностное распределение характеризуется математическим ожиданием (expected value). Матожидание — это среднее значение (mean value) случайной величины X, взвешенное по вероятности каждого из возможных значений.

$$ {\mathbb E}[X] = \sum_{i=1}^{\infty} x_i p_i $$

В случае бросания игральной кости расчет будет выглядеть следующим образом.

$$ {\mathbb E}[X] = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} = 3.5 $$

Для равномерного распределения есть и сокращенная формула.

$$ {\mathbb E}[X] = \frac{a+b}{2} = \frac{1+6}{2} = 3.5 $$

На Питоне мы можем сложить результаты поэлементного умножения.

1	np.sum(rel_freq * elements).round(2)

3.5

Кроме того, можно использовать скалярное произведение.

1	np.dot(rel_freq, elements).round(2)

3.5

Посмотрим на среднее значение сгенерированного распределения.

1	np.mean(dice)

3.50312

Дисперсия

Еще одной характеристикой вероятностного распределения является дисперсия (variance). Для равномерного распределение она вычисляется по следующей формуле.

$$ {\mathbb D}[X] = \frac{n^2-1}{12} $$

В нашем случае дисперсия равна

$$ {\mathbb D}[X] = \frac{6^{2}-1}{12} = \frac{35}{12} \approx 2,917 $$

Сравним с нашим распределением

1	np.var(dice)

1	2.9156702656

Впрочем, далеко не все дискретные распределения равномерны. Посмотрим на распределение Бернулли.

Распределение Бернулли

Многие случайные процессы характеризуются только двумя исходами. Это и выпадение орла или решки при подбрасывании монет, и успех или неудача клинического испытания. Такие процессы можно моделировать с помощью распределения Бернулли (Bernulli distribution).

Давайте рассмотрим этот процесс на практике. На этот раз мы будем подбрасывать монету, но не обычную или «честную монету», а такую, в которой вероятность выпадения решки (обозначим ее p) равна 0,7, а вероятность орла — 0,3. После каждого подбрасывания запишем получившийся результат.

В Numpy нет отдельной функции для распределения Бернулли, поэтому напишем собственную функцию.

В следующей главе я покажу, как можно использовать функцию биномиального распределения для имитации эксперимента Бернулли.

Объявим функцию bernoulli() с двумя параметрами, p и iter. Первый параметр будет отвечать за выпадение орла, второй — за количество подбрасываний.
С помощью функции np.random.rand() мы будем генерировать значение непрерывной равномерной величины (об этом опять же чуть ниже) и если получившееся значение меньше p, мы запишем, что выпала решка (1), в противном случае, что орел (0).

Посмотрим на реализацию на Питоне.

# объявим функцию bernoulli() с параметрами p, iter

def bernoulli(p, iter = 1):

# создадим пустой массив

result = np.array([])

# в цикле с количеством итераций iter

for i in range(iter):

# если значение np.random.rand() в диапазоне [0, 1) меньше или равно p

if np.random.rand() <= p:

# запишем в массив result единицу

result = np.append(result, 1)

else:

# в противном случае, запишем ноль

result = np.append(result, 0)

# в результате выполнения функции вернем массив result

return result

Вызовем эту функцию с параметрами p и iter, равными 0,7 и 10000 соответственно.

# вызовем функцию

res = bernoulli(0.7, 10000)

# выясним количество нулей и единиц в получившемся массиве

_, counts = np.unique(res, return_counts = True)

# рассчитаем относительную частоту

counts / len(res)

1	array([0.7038, 0.2962])

Посмотрим на распределение Бернулли на графике. Воспользуемся столбчатой диаграммой.

# в качестве названия столбцов передадим '0' и '1' в формате строки,

# в качестве высоты - относительную частоту значений

plt.bar(['0', '1'], counts / len(res), width = 0.98)

plt.show()

Биномиальное распределение

Пример с одинаковой вероятностью

Продолжим подбрасывать монеты, но уже не по одному разу, а по три, и каждый раз записывать результат. Всего для каждой серии испытаний (по три подбрасывания в каждой) возможны восемь исходов.

Обозначим решку через H (head), а орла через T (tail).

Вероятность каждой из комбинаций равна 1/8, так как при одном подбрасывании вероятность выпадения орла или решки одинакова (монета симметрична, fair coin).

$$ P = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} $$

Какова вероятность выпадения двух орлов (вне зависимости от порядка, в котором они выпадали)? Вначале нам нужно посмотреть, в скольких комбинациях оказалось два орла (назовем такие испытания «успехами», successes).

Таких комбинаций три (HHT, HTH, THH). Осталось количество «успехов» умножить на вероятность каждого исхода.

$$ P(X = 2) = 3 \times \frac{1}{8} = \frac{3}{8} $$

Очевидно, таким образом мы можем посчитать вероятность выпадения любого количества орлов. Например, у нас только один случай выпадения всех решек, и соответственно вероятность остаться без орлов составляет

$$ P(X = 0) = \frac{1}{8} $$

Вероятность одного и трех орлов после трех испытаний равна

$$ P(X = 1) = 3 \times \frac{1}{8} = \frac{3}{8} $$

$$ P(X = 3) = \frac{1}{8} $$

Для полноты картины замечу, что, например, P(X = 3) читается как вероятность (P) того, что случайная величина (X) примет значение три.

Теперь давайте выведем эти вероятности на график. По оси x разместим возможные значения случайной величины X, а по оси y соответствующие вероятности P(X = x). У нас получился график биномиального распределения.

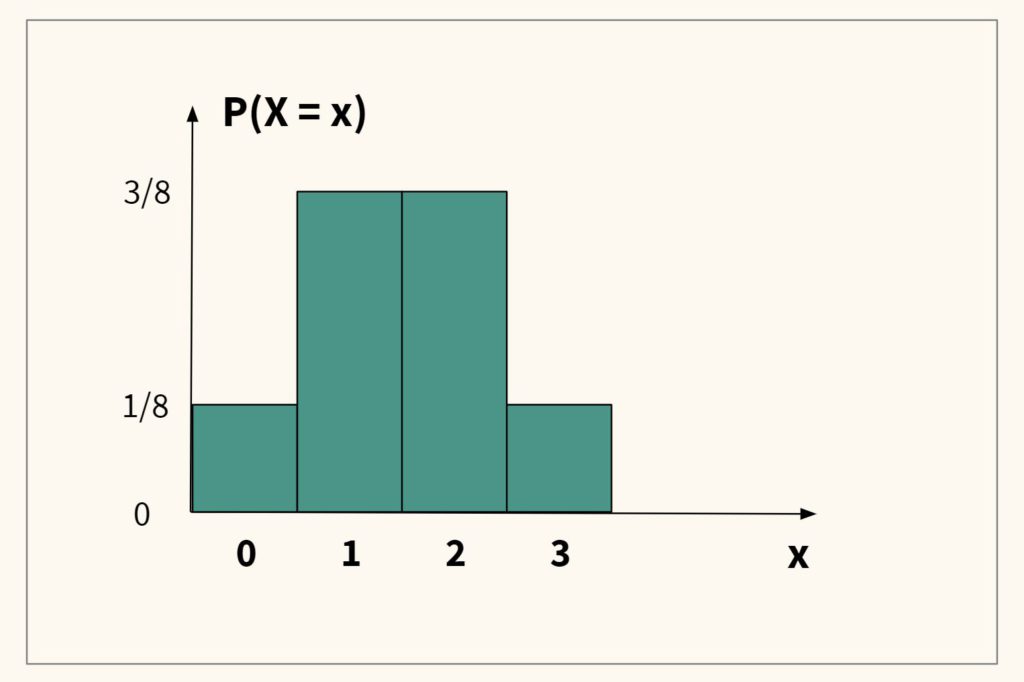
биномиальное распределение с одинаковой вероятностью (гистограмма)

Таким образом, биномиальное распределение (binomial distribution) показывает вероятность количества успехов каждой из возможных комбинаций исходов в серии одинаковых независимых испытаний Бернулли.

Пример с разной вероятностью

Давайте немного изменим условия эксперимента. На этот раз монета будет неправильной или несимметричной (biased coin) и вероятность выпадения решки составит 0,7, а орла — 0,3. Построим дерево вероятностей (tree diagram).

биномиальное распределение с разной вероятностью

Обратите внимание, несимметричность монеты повлияла на результат. Рассчитаем вероятности выпадения одного и двух орлов.

$$ P(X = 1) = 3 \times 0,063 = 0,189 $$

$$ P(X = 2) = 3 \times 0,147 = 0,441 $$

Аналогично рассчитаем вероятность, что орел вообще не выпал и что выпали только орлы.

$$ P(X = 0) = 0,027 $$

$$ P(X = 3) = 0,343 $$

Построим такое биномиальное распределение на графике.

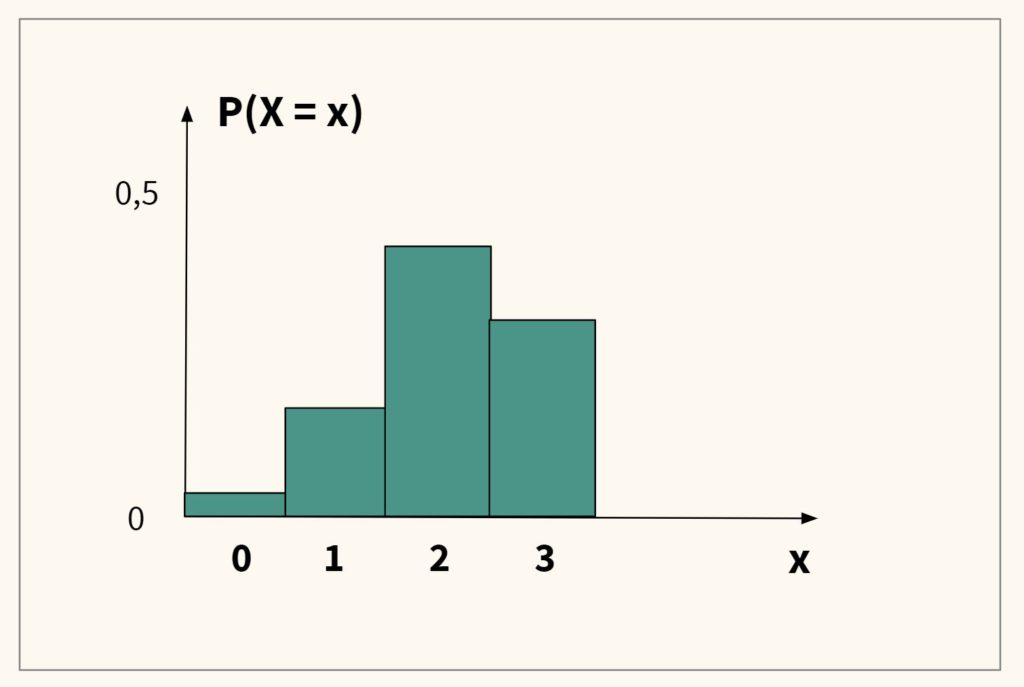
биномиальное распределение с разной вероятностью (гистограмма)

Обратите внимание, распределение несимметрично с более пологой частью слева. Еще говорят, что распределение скошено влево (skewed left). Если бы вероятность выпадения решки была 0,3, а орла — 0,7, то распределение имело бы обратную форму и было скошено вправо (skewed right).

Формула биномиального распределения

Пока мы бросали монету по три раза, то вероятность любой комбинации исходов несложно посчитать с помощью дерева вероятностей. При этом если подбрасывать, например, 10 раз, количество вариантов достигнет 2¹⁰ = 1024. Для такого распределения понадобится формула.

Возможно вы обратили внимание, что для выведения формулы нам нужно два компонента:

количество возможных комбинаций
вероятность каждой из них

Количество каждой из возможных комбинаций можно найти с помощью треугольника Паскаля. Например, при трех подбрасываниях (n = 3), мы видим, что количество возможных комбинаций будет равно {1, 3, 3, 1}, что соответствует нашему дереву вероятностей.

Можно также воспользоваться формулой биномиальных коэффициентов, в которой через n мы обозначим количество подбрасываний, а через k — количество «успехов» (выпадений орлов).

$$ \binom{n}{k} = \frac{n!}{k!(n-k)!} $$

Например, убедимся, что выпадение двух орлов (k = 2) при трех подбрасываниях (n = 3) возможно в трех комбинациях.

$$ \binom{3}{2} = \frac{3!}{2!(3-2)!} = 3 $$

Одновременно, нам нужно понимать вероятность каждой комбинации. Ее можно рассчитать по формуле

$$ p^k (1-p)^{n-k} $$

В данном случае мы возводим вероятность успеха (p) в степень количества успехов (k) и вероятность неудачи (1−p) в степень количества неудач (n−k). Например, если вероятность выпадения орла (p) равна 0,7, то вероятность выпадения двух орлов (k = 2) в трех бросках (n = 3) равна

$$ 0,7^2 (1-0,7)^{3-2} = 0,49 \times 0,3 = 0,147 $$

Остается перемножить количество комбинаций и вероятность каждой из них

$$ P(X = 2) = 3 \times 0,147 = 0,441 $$

Таким образом, вся формула целиком выглядит так

$$ P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} $$

Эта же формула описывает функцию вероятности (probability mass function, pmf) биномиального распределения.

Матожидание и дисперсия

Матожидание рассчитывается по формуле

$$ {\mathbb E}[X] = np $$

Например, после трех бросков мы можем ожидать, что в среднем орел выпадет 3 x 0,7 = 2,1 раза. Дисперсию можно рассчитать через

$$ {\mathbb D}[X] = np(1-p) \rightarrow {\mathbb D}[X] = 3 \times 0,7 \times (1-0,7) = 0,63 $$

Биномиальное распределение на Питоне

Выполним эти же расчеты с помощью Питона. Функция np.random.binomial() принимает три параметра:

n — количество испытаний в одном эксперименте (например, подбрасываний монеты)
p — вероятность успеха (например, выпадения орла)
size — количество экспериментов (серий по n подбрасываний)

# зададим точку отсчета

np.random.seed(42)

# и проведем 1 000 000 экспериментов (size) по три подбрасывания монеты (n)

# с вероятностью выпадения орла 0,7 (p)

res = np.random.binomial(n = 3, p = 0.7, size = 1000000)

# посмотрим на первые 10 значений

res[:10]

1	array([2, 1, 2, 2, 3, 3, 3, 1, 2, 2])

Теперь посмотрим, сколько раз выпали ноль, один, два или три орла и рассчитаем относительную частоту каждого из значений.

1 2	_, counts = np.unique(res, return_counts = True) counts / len(res)

1	array([0.027142, 0.188935, 0.441131, 0.342792])

Как вы видите, при достаточно большом количестве экспериментов эмпирическая вероятность приблизилась к рассчитанной выше теоретической вероятности.

Посмотрим на распределение на графике.

1 2	plt.bar(['0', '1', '2', '3'], counts / len(res), width = 0.98) plt.show()

Рассчитаем среднее значение и дисперсию.

1 2	# рассчитаем среднее значение np.mean(res)

2.099573

1 2	# рассчитаем дисперсию np.var(res)

1	0.6303802176710002

Дополнительно, как и обещал, покажу как можно повторить эксперимент Бернулли с помощью функции np.random.binomial(). Для этого достаточно указать параметр n = 1 (то есть только одно подбрасывание).

np.random.seed(42)

# вызовем функцию с параметром n = 1

res = np.random.binomial(n = 1, p = 0.7, size = 1000000)

# выясним количество нулей и единиц в получившемся массиве

_, counts = np.unique(res, return_counts = True)

# посмотрим на относительную частоту значений

counts / len(res)

1	array([0.30021, 0.69979])

Выведем распределение на графике.

1 2	plt.bar(['0', '1'], counts / len(res), width = 0.98) plt.show()

Существуют и другие дискретные вероятностные распределения, например, геометрическое распределение или распределение Пуассона. Теперь перейдем к вероятностным распределениям непрерывной случайной величины.