Описательная статистика | Вводный курс ML

Машинное обучение

Описательная статистика

Все курсы > Вводный курс > Занятие 8

На прошлом занятии мы уже начали работать с данными и статистикой. Сегодня мы продолжим этот путь.

Какая бывает статистика

виды статистики: описательная статистика и статистический вывод

Иногда данных бывает так много, что чтобы увидеть картину в целом, их нужно обобщить. Этим занимается описательная статистика (Descriptive Statistics).

Причем обобщить правильно, чтобы наши измерения отражали реальное положение вещей. Известное высказывание Марка Твена о том, что «существует три вида лжи: ложь, наглая ложь и статистика», верно лишь в той степени, в которой мы сознательно или по незнанию искажаем сбор и описание данных. Сама статистика здесь ни при чем.

Кроме того, довольно часто нам нужно составить представление о явлении, охватить которое наблюдением мы не можем. Например, мы хотим понять насколько эффективно новое лекарство, но обследовать всех, кто его принял, не представляется возможным. Статистический вывод (Statistical Inference) позволяет сделать обоснованное предположение о явлении в целом по ограниченному числу наблюдений.

На этом занятии мы поговорим про описательную статистику, на следующем — займемся статистическим выводом.

Вначале откроем ноутбук к этому занятию⧉

Начнем с того, что данные (или как еще говорят переменные) бывают двух видов, категориальные и количественные.

типы данных: категориальные и количестенные переменные

1. Категориальные (качественные) данные

Это данные, которые можно отнести к какой-то категории (categorical data). Например, людей можно разделить на мужчин и женщин, на детей и взрослых. Категориями могут быть профессии, группа крови, принадлежность к политической партии. Разделение книг по жанрам или потребителей по степени их удовлетворенности будет категориальной переменной.

Пример: сколько студентов учится на каждом курсе университета

Единицей наших данных в этом примере будут студенты. Категорией будет курс.

Самое простое, что мы можем сделать при работе с такой переменной, это взять наблюдения каждой категории и посчитать их количество. График, который помогает оценить такие данные, называется столбчатой диаграммой (bar chart).

Мы уже знакомы с библиотекой Matplotlib. Ей и воспользуемся.

Результат:

столбчатая диаграмма: распределение студентов по курсам университета

Какой вывод можно сделать на основе этих данных? До пятого курса доходят не все. Причем больше всего студентов отчисляется после второго курса, руководству вуза стоит обратить внимание именно на этих студентов. Без графика картина была бы не так очевидна.

Теперь про количественные данные.

2. Количественные данные

Примером количественных данных (quantitative data) может быть рост и вес людей, расстояние до объекта, уровень дохода и цена товара. Количественные данные — это всегда какое-то числовое значение, не категория.

Пример: рост мужчин в России

Давайте будем спрашивать у мужчин на улице, какой у них рост и поместим эти данные в питоновский список:

Теперь для удобства создадим группы или интервалы (bin) роста и посчитаем, сколько людей попадет в каждый из этих интервалов. В этом нам поможет функция hist из той же библиотеки Matplotlib.

Количество интервалов можно выбирать произвольно. Обычно останавливаются на том количестве, которое обеспечивает наглядность данных. В нашем случае интервалов будет 10. Ширину интервала Питон подберет сам.

Посмотрим на результат:

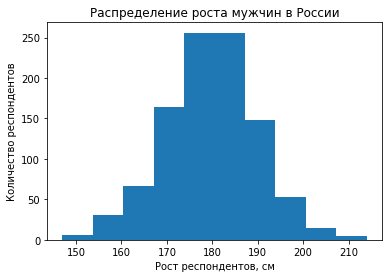
гистограмма, распределение роста мужчин в России.

Построенный нами график называется гистограммой (histogram).

Что мы можем сказать по этому графику? Средний рост мужчин вероятно составляет 180 см и довольно мало мужчин ростом ниже 160 см и выше двух метров. Картина выглядит логичной.

Обратите внимание, что столбчатая диаграмма и гистограмма — это два разных графика. Первый нужен для представления категориальных данных, второй — для количественных. Их часто путают.

В то же время, к сожалению, «на глаз» дать более точную оценку нашим данным будет сложно. Нам нужны количественные измерения. Давайте посмотрим, что можно измерить.

измерение количественных данных в описательной статистике: среднее и разброс (отклонение)

Поиск среднего

Первое количественное измерение, которое мы можем провести, это найти среднее.

Среднее арифметическое

С одним из видов средних значений, средним арифметическим, мы уже познакомились на прошлом занятии. Посчитаем его для наших данных.

Напомню, что среднее арифметическое (mean) — это сумма всех значений, поделенная на их количество. Для первых пяти значений среднее арифметическое будет следующим:

$$ \frac {185 + 179 + 186 + 195 + 178}{5} = 184.6 $$

Приведу также и формулу. Постепенно нам нужно будет привыкать ими пользоваться.

$$ \overline{x} = \frac {1}{n} \sum^{n}_{i=1} x_i= \frac {x_1 + x_2 + \dots + x_n}{n} $$

Для 1000 значений посчитать среднее арифметическое вручную сложнее. Воспользуемся Питоном и новым для нас модулем statistics, который вычислит среднее для питоновского списка.

Результат:

Медиана

Медиана (median) — еще одна мера среднего. Рассчитывают ее так: выстраивают все данные от меньшего к большему и берут то значение, которое находится посередине. Вычислим медиану для первых пяти значений. Для этого,

  1. Проранжируем наши данные по возрастанию: 178, 179, 185, 186, 195
  2. Медианой будет третий (средний) элемент списка. Этот элемент равен 185 сантиметрам

Чтобы рассчитать медиану для всех значений, снова воспользуемся модулем statistics.

Результат:

Мода

Третьей мерой среднего является мода (mode). Ее рассчитать несложно. Это просто наиболее часто встречающееся значение.

В пяти приведенных значениях моды нет. Все значения разные. При этом, если бы первое значение было равно 179, то именно это значение и стало бы модой. Оно встречалось бы дважды: 179, 179, 185, 186, 195.

Рассчитаем моду для всего набора данных:

Результат:

Зачем столько средних?

Возможно вам стало интересно, зачем столько измерений одного и того же. Дело в том, что иногда выбор типа среднего может очень сильно повлиять на наши выводы.

Допустим, у нас есть пять человек, доход которых (в тысячах рублей) мы поместили в питоновский список и рассчитали среднее арифметическое и медиану:

Результат:

Теперь предположим, что человек, получавший 100 тысяч рублей получил повышение, и теперь зарабатывает 200 тысяч. Означает ли это, что доход всех людей в среднем вырос? Среднее арифметическое и медиана дадут разные ответы на этот вопрос:

Результат:

Как мы видим, среднее арифметическое выросло очень существенно, медиана осталась прежней. Именно медиана в данном случае дает более адекватную оценку среднего, потому что в действительности доход большинства людей не изменился, и мы не можем говорить, что они стали богаче только потому, что один человек стал получать больший доход.

Обращайте на это внимание, когда будете слышать в новостях о росте средней зарплаты. Очень важно знать каким средним этот рост посчитали.

Разброс или отклонение от среднего

Помимо среднего значения нам было бы интересно узнать насколько данные отклоняются от среднего. Посмотрите на две гистограммы ниже, у них одинаковое среднее (примерно равно нулю) и одинаковое количество наблюдений (по 1000 в каждом), но разве эти графики идентичны? Нет, и виной всему разный разброс данных у variable_a и variable_b. В первом случае разброс от −5 до 5, во втором — от −10 до 10.

две гистограммы, пример одинакового среднего значения и разных СКО.

На этом занятии мы не будем считать разброс вручную, отложим это знакомство до последующих курсов. Скажу лишь, что наиболее популярной мерой разброса или отклонения от среднего является среднее квадратическое отклонение или СКО (standard deviation).

Для нашей 1000 наблюдений роста мужчин мы рассчитаем СКО с помощью Питона.

Результат.

Другими словами, рост отклоняется от среднего примерно на 10 см.

Интересный факт, почти все наблюдения укладываются в три стандартных отклонения в обе стороны от среднего. В нашем случае, они находятся в диапазоне от 180 − 3 х 10 и 180 + 3 х 10 или в диапазоне от 150 до 210 см.

наблюдения попадают в +/- три стандартных квадратических отклонения от среднего

Это все, что я хотел вам рассказать сегодня. Надеюсь, было интересно.

Подведем итог

Итак, вы узнали про описательную статистику и статистический вывод.

Кроме этого, вы познакомились с категориальными и количественными данными.

  • Для визуализации категориальных данных мы использовали столбчатую диаграмму
  • Количественные данные мы:
    • Во-первых, представили с помощью гистограммы
    • И, во-вторых, смогли описать с помощью точных метрик, средних значений (среднего арифметического, медианы и моды) и разброса (среднеквадратического отклонения)

Вопросы и упражнения для закрепления

Облигациям присваивают рейтинг надежности: высокий, средний и низкий. Это категориальные или количественные данные?

Посмотреть правильный ответ

Вы записывали показания измерительного прибора (пусть это будет штангенциркуль) и собрали следующие данные: 22, 24, 18, 17, 22 мм. Рассчитайте среднее арифметическое, медиану и моду.

Посмотреть правильный ответ

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

На следующем занятии мы посмотрим, что такое статистически значимый вывод.

Ответы на вопросы

Вопрос. Почему в расчете среднего арифметического используется код np.round(statistics.mean(height), 2), а при расчетах медианы и моды соответственно statistics.median(height) и statistics.mode(height).

В моем понимании код для вычисления СА должен быть statistics.mean(height)

Ответ. Конечно можно и так, функция np.round() просто округляет значение.