Все курсы > Вводный курс > Занятие 18
Компьютерное зрение (computer vision) — это область, занимающаяся анализом фото и видео изображений. Построенные на основе этого анализа модели помогают смартфонам узнавать своих владельцев, дорожным камерам распознавать номера автомобилей, а роботам объезжать препятствия.
На этом занятии мы рассмотрим основы черно-белого и цветного цифрового изображения, способы обработки изображений в Питоне, а также начнем изучать такую область компьютерного зрения, как классификация изображений.
Работа с изображениями в Питоне
Любое цифровое изображение — это по сути матрица, а в случае Питона, массив Numpy, в котором положение пикселей (составных частей, pixel или picture element) задано координатами.

Значениями такой матрицы будут оттенки цветов. Сочетание пикселей разных оттенков и создает цифровое изображение.
Для работы с изображениями мы, главным образом, будем использовать библиотеку scikit-image.
По традиции вначале откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 |
# импортируем имеющиеся в библиотеке skimage фотографии from skimage import data # и уже известные нам библиотеки matplotlib и numpy import matplotlib.pyplot as plt import numpy as np |
Черно-белые изображения
В случае черно-белого изображения, или правильнее сказать, изображения в оттенках серого (grayscale image), речь идет об одном слое матрицы.

Для каждого пикселя у нас есть 256 оттенков от черного (0) до белого (255). С точки зрения Питона, речь идет о двумерном массиве (координаты пикселя по вертикали и горизонтали).
Вначале давайте импортируем уже встроенное в эту библиотеку изображение и выведем его на экран.
|
1 2 3 4 5 |
# импортируем черно-белую фотографию camera_img = data.camera() # воспользуемся функцией imshow для показа изображения plt.imshow(camera_img, cmap = 'gray') |

По умолчанию, imshow преобразует черно-белые фото в цветные. Чтобы этого избежать, нужно указать параметр цветовой схемы cmap = 'gray'.
|
1 2 |
# посмотрим на тип данных type(camera_img) |
|
1 |
numpy.ndarray |
Повторюсь, отдельного класса для изображений в Питоне нет, мы работаем с массивами Numpy.
Посмотрим на его размерность. Должно быть два измерения.
|
1 2 |
# размерность (вертикаль х горизонталь) camera_img.shape |
|
1 |
(512, 512) |
А также на общее количество пикселей.
|
1 2 |
# 512 х 512 camera_img.size |
|
1 |
262144 |
Мы можем вывести тип значения нашей матрицы, общий диапазон оттенков, а также значение (оттенок) конкретного пикселя.
|
1 2 |
# каждое значение состоит из целых чисел длиной 8 бит camera_img.dtype |
|
1 |
dtype('uint8') |
|
1 2 |
# диапазон этого значения (т.е. оттенков), как мы и говорили, от черного (0) до белого (255) camera_img.min(), camera_img.max() |
|
1 |
(0, 255) |
|
1 2 |
# задав координаты конкретного пикселя, мы можем посмотреть его оттенок camera_img[50,50] |
|
1 |
207 |
Для того чтобы вывести этот оттенок на экран, воспользуемся библиотекой PIL (Python Imaging Library).
|
1 2 3 4 5 6 7 |
# посмотрим, что это за цвет, создав картинку в библиотеке PIL from PIL import Image # mode = 'L' указывает, что это ч/б изображение, размером 200 х 100 # и оттенком серого как раз 158 sample1 = Image.new(mode = 'L', size = (200, 100), color = 158) sample1 |

Цветные изображения
У цветного изображения (color image) таких слоев, или правильнее говорить каналов (channels), три: красный, зелёный и синий (red, green, blue или RGB).
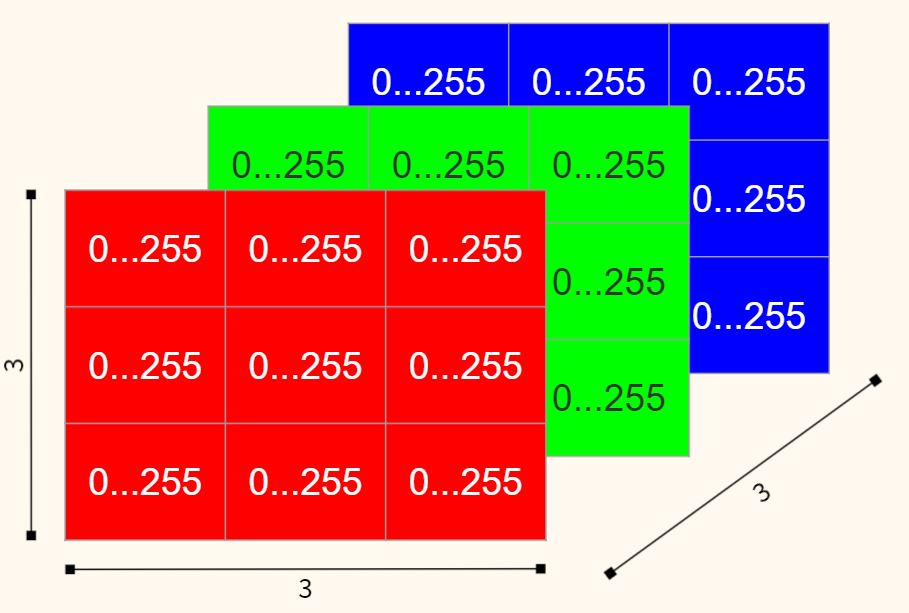
Комбинация интенсивности этих цветов и определяет цвет каждого пикселя. Вот несколько примеров.
Теперь поработаем с цветными изображениями в Питоне.
|
1 2 3 4 5 |
# импортируем цветную фотографию cat_img = data.chelsea() # и выведем ее на экран plt.imshow(cat_img) |

|
1 2 |
# посмотрим на размерность cat_img.shape |
|
1 |
(300, 451, 3) |
В данном случае измерений у массива Numpy уже три, координата по вертикали, по горизонтали и слой. Значениями будет интенсивность каждого из трёх цветов (также от 0 до 255).
|
1 2 |
# аналогично черно-белому изображению, мы можем посмотреть оттенки красного, зелёного и синего конкретного пикселя cat_img[50, 50] |
|
1 |
array([138, 98, 63], dtype=uint8) |
|
1 2 3 |
# опять же воспользуемся PIL для визуализации этого цвета sample2 = Image.new(mode = 'RGB', size = (200, 100), color = (138, 98, 63)) sample2 |

Каждый из трёх базовых цветов или каналов можно изолировать.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# функция subplots дает возможность вывести сразу несколько изображений # в качестве параметров передаем количество строк и столбцов сетки изображений (1 x 3) # и размер графиков fig, ax = plt.subplots(1, 3, figsize = (12, 4)) # и выводим каждое изображение по отдельности # сначала только красные оттенки, слой [0] # также нужно принудительно задать cmap = 'Reds' ax[0].imshow(cat_img[:,:,0], cmap = 'Reds') # также зададим заголовок ax[0].set_title('Оттенки красного') # потом только зеленые, слой [1] ax[1].imshow(cat_img[:,:,1], cmap = 'Greens') ax[1].set_title('Оттенки зеленого') # и наконец только синие, слой [2] ax[2].imshow(cat_img[:,:,2], cmap = 'Blues') ax[2].set_title('Оттенки синего'); |

Если эти картинки наложить друг на друга, мы восстановим исходное изображение.
Гистограмма
Как чёрно-белое, так и цветное изображение можно визуализировать с помощью гистограммы. По горизонтали будут отложены оттенки от 0 до 255, а по вертикали количество пикселей каждого из оттенков. Начнем с черно-белого.
|
1 2 3 4 5 |
# воспользуемся еще одной библиотекой популярной библиотекой OpenCV import cv2 # и создадим гистограмму с помощью calcHist hist_gray = cv2.calcHist([camera_img], [0], None, [256], [0, 256]) |
Функции calcHist мы передаем следующие параметры:
- image: само изображение [camera_img]
- channels: для ч/б фотографии это [0]
- mask: так как мы строим гистограмму всего изображения, то фильтр или срез (mask) равен None
- histSize: количество интервалов (bins) [256]
- ranges: диапазон оттенков [0,256]
|
1 |
plt.plot(hist_gray) |
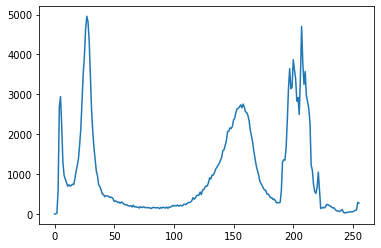
Аналогичным образом создадим гистограмму цветного изображения.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# цветной гистограмме мы передадим параметры в формате "синий, зеленый, красный" color = ('b','g','r') # в цикле for пройдемся по цветам ('b','g','r') # и соответствующим каналам [0, 1, 2] с помощью enumerate for channel, col in enumerate(color): # здесь параметры схожи, только каналов теперь три hist_color = cv2.calcHist([cat_img], [channel], None, [256], [0, 256]) # строим на каждой итерации цикла по кривой и берем для нее цвет из color plt.plot(hist_color, color = col) |
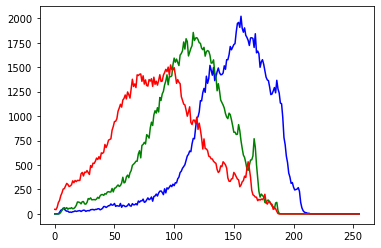
Гистограмма может использоваться, например, при поиске порогового значения (threshold) в процессе обработки изображения (об этом ниже).
Обработка изображений
Начнем с простых операций. Например, мы можем вырезать часть изображения по координатам.
|
1 2 3 |
# например, покажем только глаза кошки eyes = cat_img[70:185, 115:355] plt.imshow(eyes) |

Кроме того, мы можем изменить цвет конкретного пикселя или закрасить целую область.
|
1 2 3 |
# например, создать черную полосу, задав цвет 0 (черный) первым 40 строкам массива camera_img[:40] = 0 plt.imshow(camera_img, cmap = 'gray') |

Также ожидаемо библиотека skimage позволяет преобразовывать цветные изображения в черно-белые.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# библиотека skimage также позволяет преобразовывать цветные изображения в черно-белые from skimage.color import rgb2gray # импортируем еще одно фото из библиотеки color_img = data.astronaut() # воспользуемся функцией rgb2gray grayscale_img = rgb2gray(color_img) # снова возьмем уже знакомую функцию subplots fig, ax = plt.subplots(1, 2, figsize = (8, 4)) # выведем первое изображение и зададим заголовок ax[0].imshow(color_img) ax[0].set_title('Цветное') # для ч/б изображения не забудем про параметр cmap = 'gray' ax[1].imshow(grayscale_img, cmap = 'gray') ax[1].set_title('Черно-белое') plt.show() |

|
1 2 |
# проверим print (color_img.shape, grayscale_img.shape) |
|
1 |
(512, 512, 3) (512, 512) |
Так как наши изображения не что иное, как матрицы, мы можем применять к ним матричные вычисления и благодаря этому трансформировать их. В частности, матрицы можно транспонировать (т.е. каждую строчку исходной матрицы записать в виде столбцов в том же порядке).

Если транспонировать первые две оси цветного изображения (не трогая при этом третью, цветовую ось) картинка повернется.
|
1 2 3 |
# по большому счету, меняем местами 0 и 1 color_img = np.transpose(color_img, (1, 0, 2)) plt.imshow(color_img) |

Помимо этого, решая задачи сегментации изображения (то есть выделения однородных областей, image segmentation), мы можем применить пороговое преобразование (image thresholding). Например, для того чтобы разделить передний и задний план изображения.
На практике мы задаем некий порог, и все пиксели, значение (оттенок) которых ниже порога, делаем черными, а выше — белыми. Таким образом, мы создаем по-настоящему черно-белое изображение (binary image).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# вновь импортируем ч/б изображение camera_img_2 = data.camera() # если значение пикселя ниже 87, сделаем его черным, выше - белым binary = camera_img_2 > 87 # теперь сравним исходное изображение и изображение после преобразования fig, ax = plt.subplots(1, 2, figsize = (8, 4)) # выведем первое изображение и зададим заголовок ax[0].imshow(camera_img_2, cmap = 'gray') ax[0].set_title('До') # для ч/б изображения не забудем про параметр cmap = 'gray' ax[1].imshow(binary, cmap = 'gray') ax[1].set_title('После') plt.show() |

На гистограмме это бы выглядело следующим образом.
|
1 2 3 4 5 |
# воспользуемся уже известной функцией calcHist t_hist = cv2.calcHist([camera_img_2], [0], None, [256], [0, 256]) # и добавим прямую с пороговым значением красного цвета plt.axvline(87, color = 'r') plt.plot(t_hist) |
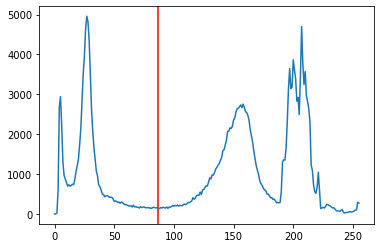
Вопрос поиска оптимального порогового значения выходит за рамки вводного курса.
Классификация изображений на примере датасета MNIST
Классификация изображений (image classification) — это задача машинного обучения с учителем. У нас есть набор изображений (наши признаки) и описание того, что представлено на этих изображениях (наша целевая переменная).
Для наших целей мы возьмём классический датасет MNIST, содержащий изображения написанных от руки цифр от 0 до 9.

После обучения модель сможет самостоятельно определять, что представлено на изображении.
Обращу ваше внимание на то, что в данном случае классов уже не два, как было в случае с датасетом о раке груди, а десять (т.е. речь идёт о мультиклассовой классификации).
В качестве алгоритма мы будем использовать метод опорных векторов (support vector machine или SVM).
Про метод опорных векторов (SVM)
Принцип этого классификатора заключается в том, чтобы построить плоскость (а вернее гиперплоскость, потому что мы работаем в многомерном пространстве) между несколькими точками каждого класса. Эти точки называются опорными векторами (support vectors).
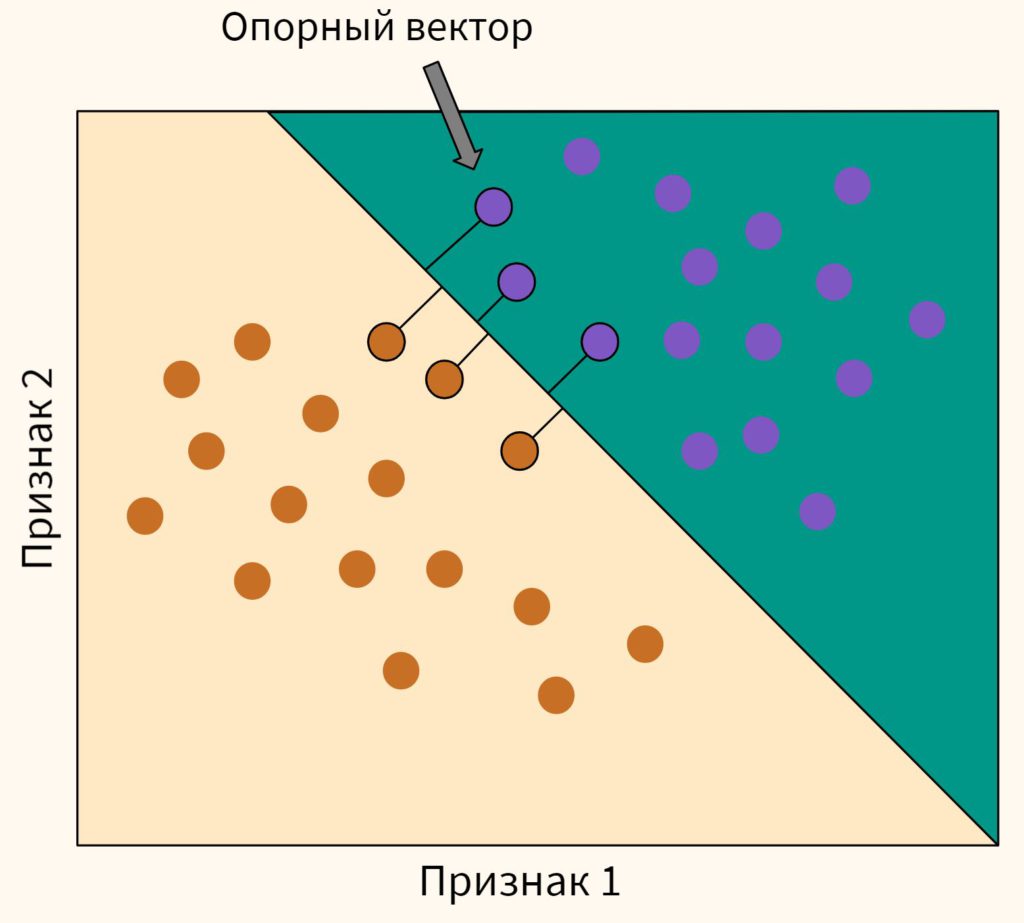
Плоскость строится таким образом, чтобы максимизировать «зазор» или расстояние между опорными векторами.
В случае если линейную плоскость провести невозможно, алгоритм предварительно трансформирует данные так, чтобы их все-таки можно было разделить с помощью гиперплоскости, т.е. линейно.

Это называется kernel trick (метод ядра). Помимо возведения в квадрат существуют и другие функции ядра.
Практика
Для начала импортируем необходимые библиотеки и сам набор данных из библиотеки Scikit-learn.
|
1 2 3 4 5 6 |
# импортируем датасеты, модуль SVM, метрики и функцию train_test_split from sklearn import datasets, svm, metrics from sklearn.model_selection import train_test_split # загрузим данные digits = datasets.load_digits() |
Посмотрим, что внутри. Традиционно для Scikit-learn встроенный набор данных представляет собой объект Bunch. Вот его компоненты.
|
1 |
digits.keys() |
|
1 |
dict_keys(['data', 'target', 'target_names', 'images', 'DESCR']) |
Изображения хранятся в компоненте images. Всего у нас 1797 изображений.
|
1 |
len(digits.images) |
|
1 |
1797 |
Каждое изображение представлено двумерным массивом 8 x 8 (что соответствует 64 пикселям).
|
1 |
digits.images[0].shape |
|
1 |
(8, 8) |
Сам массив выглядит следующим образом.
|
1 2 |
# выведем матрицу первого изображения digits.images[0] |
|
1 2 3 4 5 6 7 8 |
array([[ 0., 0., 5., 13., 9., 1., 0., 0.], [ 0., 0., 13., 15., 10., 15., 5., 0.], [ 0., 3., 15., 2., 0., 11., 8., 0.], [ 0., 4., 12., 0., 0., 8., 8., 0.], [ 0., 5., 8., 0., 0., 9., 8., 0.], [ 0., 4., 11., 0., 1., 12., 7., 0.], [ 0., 2., 14., 5., 10., 12., 0., 0.], [ 0., 0., 6., 13., 10., 0., 0., 0.]]) |
Давайте посмотрим на первые четыре изображения.
|
1 2 3 4 5 6 7 8 9 10 11 |
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, digits.images, digits.target): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = 'gray') # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f'Target: {label}') |
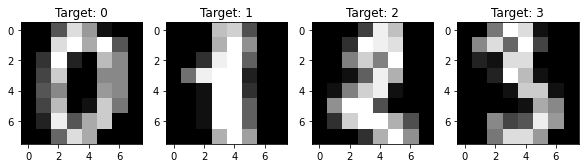
Теперь необходимо подготовить данные. В первую очередь, двумерные матрицы каждого изображения нужно преобразовать в одномерные.
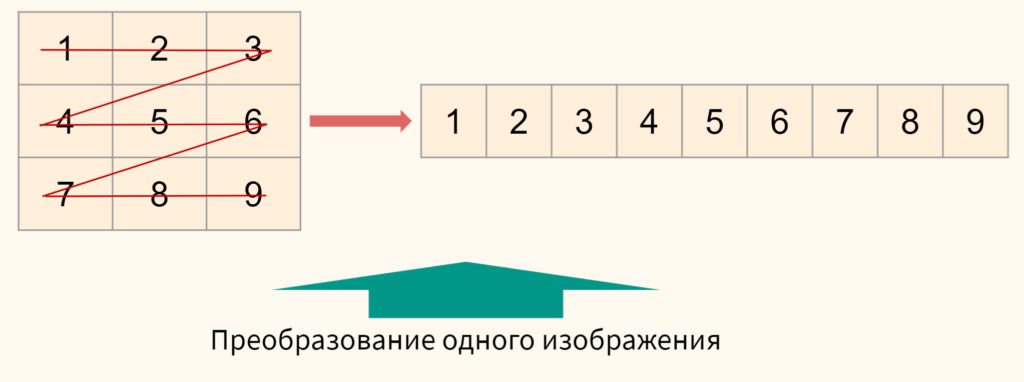
После эти матрицы нужно соединить и тогда все наши изображения поместятся в один двумерный массив.

Теперь наши цифровые изображения ничем не отличаются от стандартных данных в задачах классификации (по горизонтали отложены изображения, т.е. точки данных, по вертикали — признаки (оттенки пикселей)). На Питоне это выглядит так.
|
1 2 3 4 5 6 7 8 9 10 11 |
# превратим двумерную матрицу в одномерный массив (flatten the images) # для этого создадим переменную с количеством изображений n_samples = len(digits.images) # и превратим каждое изображение в одномерный массив # по горизонтали будут изображения, по вертикали - их признаки (пиксели) digits_t = digits.images.reshape((n_samples, -1)) # снова выведем первое изображение digits_t[0] |
|
1 2 3 4 5 |
array([ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.]) |
Как мы видим, массив «вытянулся». Удостоверимся, что мы все сделали правильно.
|
1 2 |
# посмотрим на размерность первого изображения digits_t[0].shape |
|
1 |
(64,) |
|
1 2 |
# и на размерность всего датасета digits_t.shape |
|
1 |
(1797, 64) |
В процессе обучения модели в первую очередь разобьём данные на обучающую и тестовую выборки.
|
1 2 3 4 5 6 7 8 9 10 11 |
# подготовим данные в формате X и y для наглядности X = digits_t y = digits.target # создадим объект классификатора (Support Vector Classifier) из модуля SVM svc_model = svm.SVC() # разделим выборки на обучающую и тестовую, размер тестовой выборки 30% X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42) |
Затем используем метод опорных векторов для обучения модели и формирования прогноза.
|
1 2 3 4 5 |
# обучим классификатор с помощью метода fit() svc_model.fit(X_train, y_train) # сделаем прогноз того, что представлено на картинке y_pred = svc_model.predict(X_test) |
С помощью атрубута support_ мы можем посмотреть на индексы точек (изображений), которые использовались в качестве опорных векторов при обучении модели.
|
1 2 |
# посмотрим на первые 15 индексов опорных векторов svc_model.support_[:15] |
|
1 2 |
array([ 79, 93, 126, 229, 325, 345, 402, 409, 428, 443, 455, 478, 485, 582, 608], dtype=int32) |
Если применить индексы support_ к нашему датасету, то мы выберем (отфильтруем) изображения, которые использовал классификатор.
|
1 2 |
# их было 613 X[svc_model.support_].shape |
|
1 |
(613, 64) |
Всего же в обучающей выборке в два раза больше данных.
|
1 |
X_train.shape |
|
1 |
(1257, 64) |
Для оценки качества модели вначале воспользуемся метрикой accuracy. Напомню, что она показывает долю правильных предсказаний. В случае с мультиклассовой классификацией она рассчитывается как среднее арифметическое accuracy по всем классам.
|
1 |
print("Accuracy:", np.round(metrics.accuracy_score(y_test, y_pred), 2)) |
|
1 |
Accuracy: 0.99 |
Accuracy по каждому классу будет удобно посмотреть с помощью матрицы ошибок.
|
1 2 3 4 5 6 |
# чтобы вывести матрицу ошибок, мы вначале создаем для нее пространство нужного нам размера fig, ax = plt.subplots(figsize = (8, 8)) # а затем используем метод .from_estimator() класса ConfusionMatrixDisplay, которому передаем объект модели, # данные для проверки, цветовую схему и переменную пространства, куда мы и поместим матрицу metrics.ConfusionMatrixDisplay.from_estimator(svc_model, X_test, y_test, cmap = plt.cm.Blues, ax = ax) |
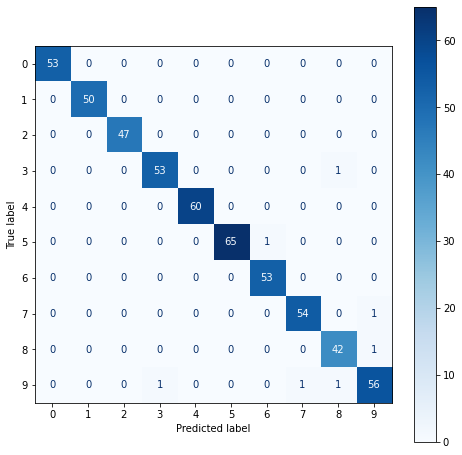
В частности, мы видим, что алгоритм дважды ошибся с цифрой 9, классифицировав ее как 7 и 8.
Мы также можем посмотреть на результат нашей работы визуально.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
fig, axes = plt.subplots(1, 4, figsize = (10, 3)) for ax, image, prediction in zip(axes, X_test, y_pred): # мы можем убрать рамку вокруг изображений ax.set_axis_off() # каждое изображение нужно восстановить до массива 2D image = image.reshape(8, 8) # в функции imshow изменим параметр cmap = plt.cm.gray_r # это обратная серой гамме цветовая схема ax.imshow(image, cmap = plt.cm.gray_r) # и выведем прогноз для каждого изображения ax.set_title(f'Prediction: {prediction}') |
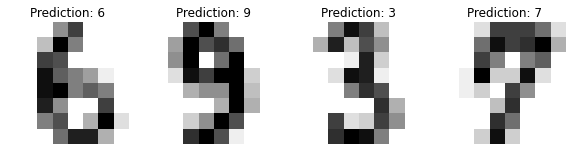
Подведем итог
Повторим пройденный материал. На сегодняшнем занятии мы узнали как устроено цифровое изображение, изучили основы обработки изображений с помощью библиотеки skimage, а также построили модель классификации изображений с помощью метода опорных векторов.
Конечно, построенная нами модель очень проста и в реальной жизни задачи классификации, а также более сложные задачи, например, распознавание изображений (image recognition) чаще решаются с помощью глубокого обучения и нейронных сетей.
Однако для первого знакомства с областью компьютерного зрения, полученных знаний должно быть достаточно.
Вопросы для закрепления
Сколько оттенков серого есть в черно-белой (grayscale) фотографии? Сколько слоев и оттенков есть в цветной фотографии?
Посмотреть правильный ответ
Ответ: в черно-белой фотографии 256 оттенков от 0 (черный) до 255 (белый). Цветная фотография имеет три слоя (красный, зеленый, синий) и каждый слой также имеет 256 оттенков.
Что такое гистограмма изображения?
Посмотреть правильный ответ
Ответ: гистограмма изображения — это график, на котором по горизонтальной оси отложены оттенки, а по вертикальной — количество пикселей каждого из оттенков.
Что такое изображение с точки зрения компьютера и Питона?
Посмотреть правильный ответ
Ответ: изображение — это матрица, в случае Питона — массив Numpy. Изначально это двумерный (ч/б) или трехмерный (цветное изображение) массив, который мы «вытягиваем» до одномерного прежде чем передать его алгоритму машинного обучения.
На следующем занятии мы познакомимся с обработкой естественного языка.
Ответы на вопросы
Вопрос. Вы не могли бы более подробно рассказать про функцию plt.subplots()? Не очень понятно, что передается в переменные fig и ax.
Ответ. Добавил небольшое объяснение и несколько примеров в конце ноутбука к этому занятию⧉.
Вопрос. Я правильно понимаю, что изображения разделяют на черно-белые, серые и цветные?
Ответ. Да, совершенно верно, на черно-белые (binary), с оттенками серого (grayscale) и цветные (color).
Вопрос. Расскажите, пожалуйста, подробнее, почему в 8 битах содержится 256 значений.
Ответ. Смотрите, предположим у нас только два бита, первый может получить значение 0 или 1 и второй также — 0 или 1. Тогда всего у нас есть четыре возможных комбинации: 00, 10, 01, 11. Рассчитать это можно, возведя 2 в степень, равную количеству имеющихся битов. Если у нас два бита, то $2^2=4.$
Аналогично, если у нас 8 битов, то $2^8=256.$
Вопрос. Можете еще раз объяснить, как используется метод .reshape()?
Ответ. Метод .reshape() применяется к массивам Numpy и меняет их размерность. Например, переводит одномерные массивы в двумерные.
Я добавил несколько примеров в дополнительных материалах в конце ноутбука⧉. Мы также будем более подробно разбираться с массивами Numpy на курсе программирования на Питоне.