Предисловие

Все курсы > Линейная алгебра > Предисловие

Начнем с того, что вспомним основные понятия тригонометрии (trigonometry).

Синус, косинус и тангенс

Пусть дан прямоугольный треугольник со сторонами $a, b, c$ и углом $\alpha$.

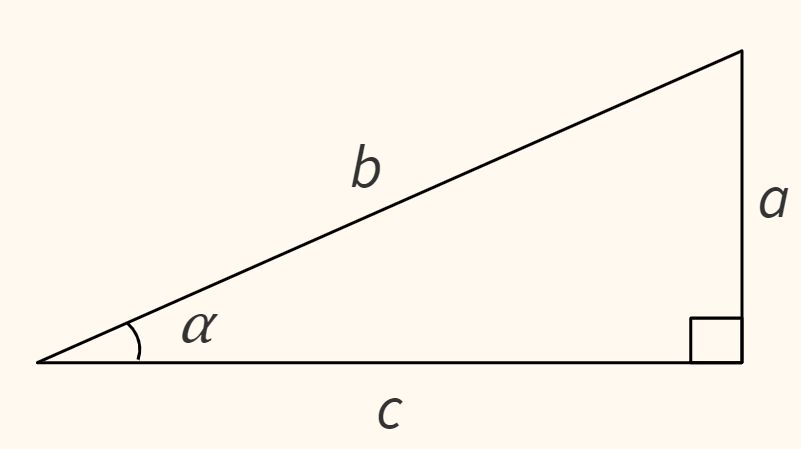
Тогда синусом (sine) угла $\alpha$ будет отношение противолежащего катета $a$ (opposite side) к гипотенузе $b$ (hypotenuse), косинусом (cosine) — отношение прилежащего катета $c$ (adjacent side) к гипотенузе, а тангенсом (tangent) — отношение противолежащего катета к прилежащему.

$$ \sin{\alpha} = \frac{a}{b} $$

$$ \cos{\alpha} = \frac{c}{b} $$

$$ \tan{\alpha} = \frac{a}{c} $$

Единичная окружность

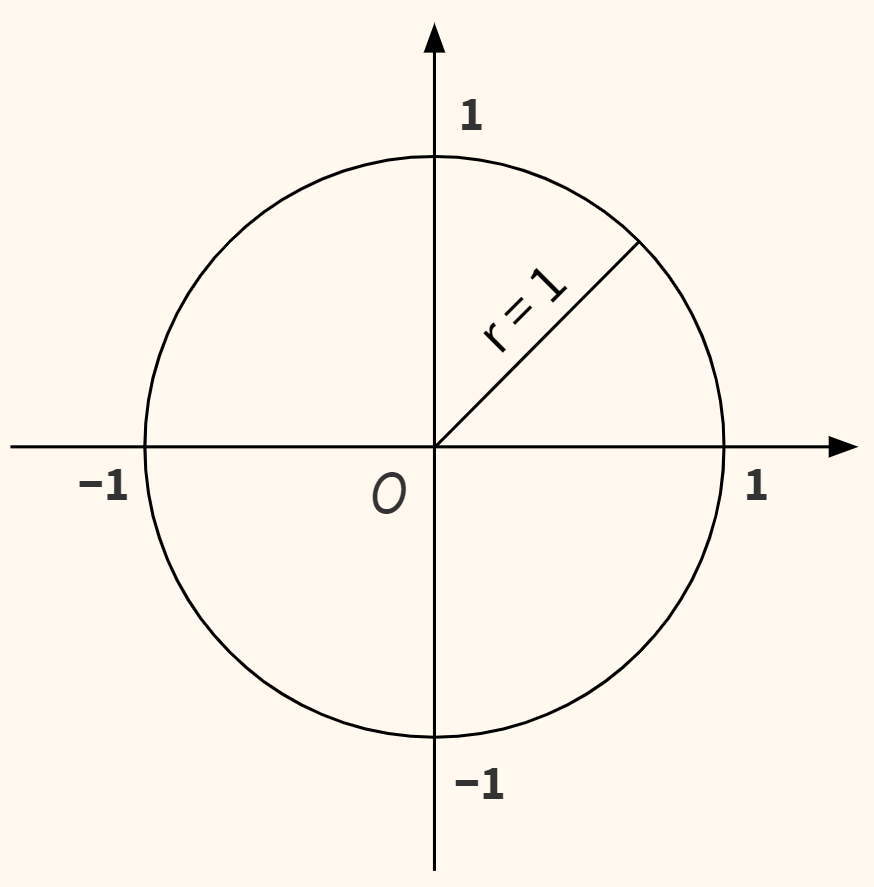
Теперь отложим треугольник в сторону и построим окружность с радиусом, равным единице (единичная окружность, unit circle). Дополнительно поместим окружность на координатную плоскость с центром $O$ в начале координат.

Углы в градусах

Такую окружность, в частности, можно разделить на 360 равных частей, называемых градусами.

Из курса дискретной математики мы уже знаем, что выбору именно такого числа частей мы, скорее всего, обязаны шестидесятеричной системе счисления.

Приведем некоторые углы, которые можно образовать с помощью оси абсцисс и луча $OA$.

Заметим, что положительный угол принято откладывать против часовой стрелки.

Длина единичной окружности

Кроме того, известно, что длина любой окружности $C$ больше ее диаметра $d$ в $\pi$ раз. То есть,

$$ C = \pi d $$

Так как диаметр в два раза больше радиуса $d =2r$, то $C = 2 \pi r$. В единичной окружности радиус по определению равен $r=1$. Длина самой окружности, таким образом, равна $C = 2 \pi$.

Как следствие, несложно найти длину дуги (arc), образованную каждым из этих углов. Например, длина дуги $L$ угла в 180 градусов равна половине длины окружности, или

$$ L = \frac{C}{2} = \frac{2\pi}{2} = \pi $$

Найдем длину дуг остальных углов, приведенных выше.

Еще раз обратим внимание на то, что $ \frac{\pi}{4}, \frac{\pi}{2}, \pi, \frac{3 \pi}{2}, 2 \pi $ определяют длину дуги и не измеряют угол.

Мера же углов, основанная на длине окружности, называется радианом.

Углы в радианах

Сколько радиусов можно отложить на окружности? Число $\pi$ приблизительно равно $3,14$. Значит на окружности можно отложить $ \frac{C}{r} = 2\pi \approx 6,28 $ радиусов.

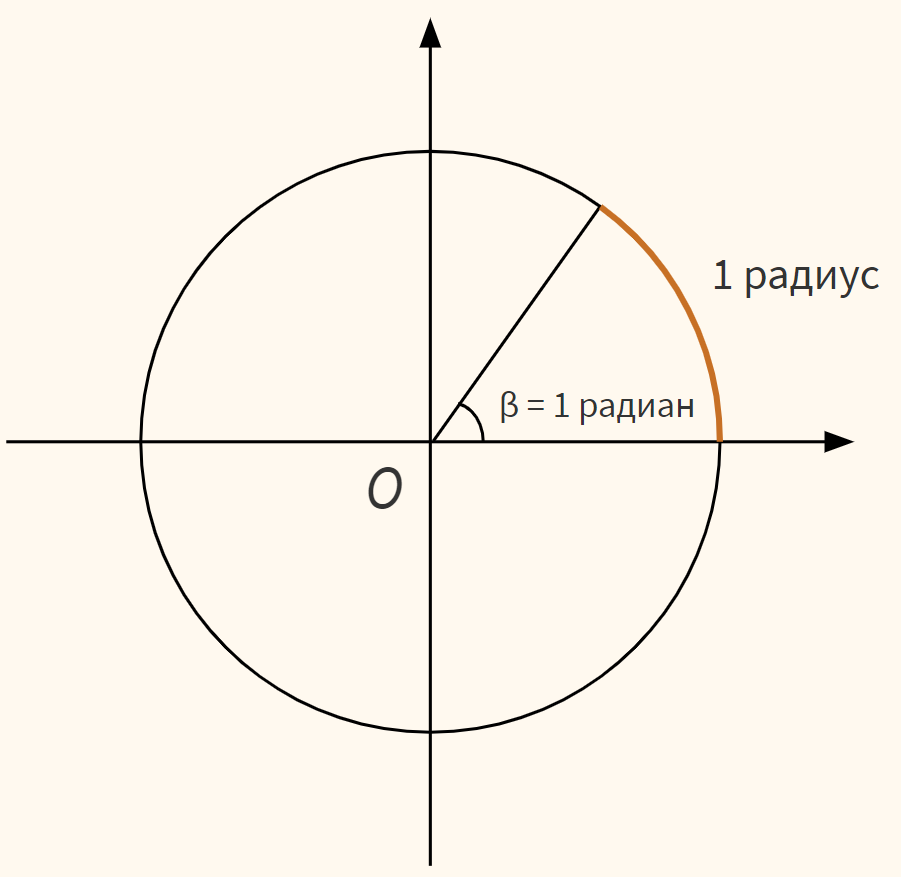
Радианом (radian) называется угол, соответствующий дуге, равной длине одного радиуса.

Радианы и градусы

Радианы в градусы

Как связаны радианы и градусы? Выше мы сказали, что в единичной окружности углу в 360 градусов соответствует длина дуги $2 \pi$ или угол в примерно $6,28$ радианов. Воспользуемся пропорцией и найдем, чему равен один радиан:

$$ \frac{360^{\circ}}{2 \pi \text{ rad} } = \frac{x}{1 \text{ rad}} $$

$$ x = \frac{1 \text{ rad} \cdot 360^{\circ}}{2 \pi \text{ rad} } \approx 57,3^{\circ} $$

Несложно перевести в градусы и другие углы, выраженные в радианах. Для этого достаточно умножить радианную меру на $\frac{360}{2 \pi}$ или $\frac{180}{\pi}$. Приведем два примера.

$$ \frac{\pi}{12} \text{ rad} = \frac{\pi}{12} \times \frac{180^{\circ}}{\pi} = 15^{\circ} $$

$$ 6,5 \text{ rad} = 6,5 \times \frac{180^{\circ}}{\pi} \approx 372,4^{\circ} $$

Градусы в радианы

Найдем, чему равен один градус в радианах.

$$ \frac{360^{\circ}}{2 \pi \text{ rad} } = \frac{1^{\circ}}{x} $$

$$ x = \frac{1^{\circ} \cdot 2 \pi \text{ rad} }{ 360^{\circ} } \approx 0,017 \text{ rad} $$

Таким образом, для перевода в радианную меру градусы необходимо умножать на $ \frac{2\pi}{360} $ или $ \frac{\pi}{180} $.

$$ 90^{\circ} = 90 \times \frac{\pi}{180} \text{ rad} = \frac{\pi}{2} \text{ rad} $$

$$ 30^{\circ} = 30 \times \frac{\pi}{180} \text{ rad} = \frac{\pi}{6} \text{ rad} $$

Угол между векторами

Окружность и треугольник

Наконец объединим прямоугольный треугольник и единичную окружность, расположив треугольник внутри окружности таким образом, чтобы

• вершина с углом $\alpha$ находилась в начале координат;
• гипотенуза совпадала с радиусом; а
• прилежащий к углу $\alpha$ катет $c$ лежал на оси абсцисс.

Так как радиус (соответствующий гипотенузе треугольника) равен единице, косинус угла $\alpha$ равен отрезку на оси $x$.

Функция косинуса

Другими словами, зная угол, мы всегда можем найти его косинус (отрезок на оси $x$), который находится в пределах от $-1$ до $1$. Такая функция называется функцией косинуса (cosine) и обозначается $ x = \cos \alpha $.

Например, косинус $45^{\circ}$ или $ \frac{\pi}{4} \text{ rad} $ равен

$$ x = \cos{45}^{\circ} = \cos{ \frac{\pi}{4} \text{ rad} } = \frac{\sqrt{2}}{2} \approx 0,71 $$

В этом несложно убедиться, так как в данном случае мы имеем дело с прямоугольным равнобедренным треугольником.

Если обозначить боковую сторону (она же $\cos \alpha$) как $l$, то по теореме Пифагора можно найти, что

$$ l^2 + l^2 = 1^2 $$

$$ 2l^2 = 1 $$

$$ l = \sqrt{ \frac{1}{2} } = \frac{ 1 }{ \sqrt{2} } = \frac{\sqrt{2}}{2} $$

Арккосинус

Если же нам дан сам отрезок, то есть косинус, то мы наоборот можем найти соответствующий угол. Такая функция обратна функции косинуса и называется арккосинусом (arc cosine), $ \alpha = \cos^{-1} x $ или $\alpha = \arccos x $.

Например, отрезок $\frac { \sqrt{3} }{2} \approx 0,87 $ соответствует углу в

$$ \alpha = \arccos \frac { \sqrt{3} }{2} = \frac{ \pi }{ 3 } \text{ rad} = 60^{\circ} $$

Векторы на плоскости

Представим, что ось абсцисс и гипотенуза/радиус являются направленными отрезками или векторами. В этом случае косинус можно использовать для нахождения угла между ними.

И действительно, рассмотрим векторы с координатами

$$ \textbf{v} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad \textbf{w} = \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{bmatrix} $$

Приведем эти векторы на графике.

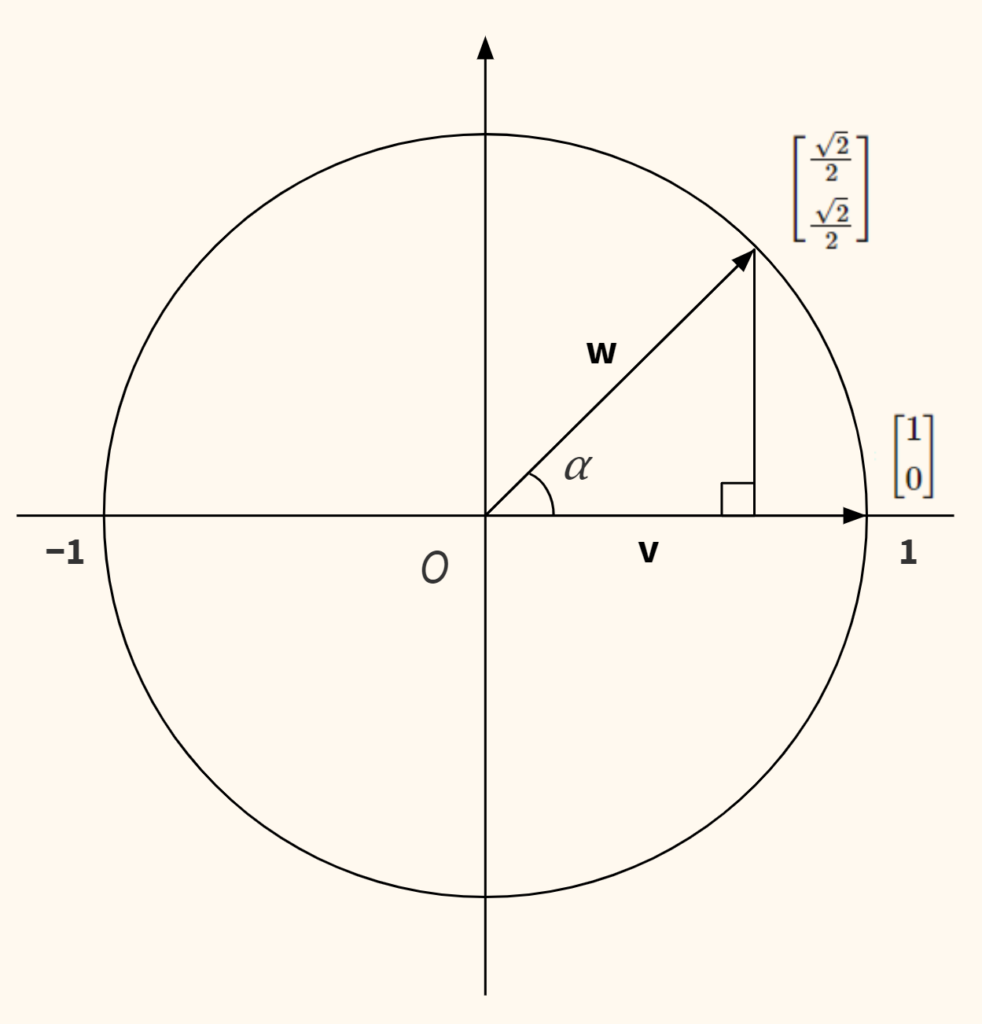
Угол между векторами

В данном случае, так как вектор $ \textbf{v} $ является осью абсцисс, то первая координата вектора $ \textbf{w} $ как раз будет косинусом угла между ними.

Зная, что $\cos \alpha = \frac{\sqrt{2}}{2}$, несложно выяснить, что

$$ \alpha = \arccos \frac{ \sqrt{2} } {2} = \frac{\pi}{4} \text{ rad} = 45^{\circ} $$

Заметим также, что это расстояние является проекцией (projection) вектора $ \textbf{w} $ на $ \textbf{v} $. К этому факту мы ещё вернёмся.

Теорема косинусов

До сих пор мы имели дело с прямоугольным треугольником. Оказывается, косинус угла можно найти для любого плоского треугольника. Сделать это можно через теорему косинусов (Law of cosines), которая обобщает теорему Пифагора.

Рассмотрим треугольник ABC.

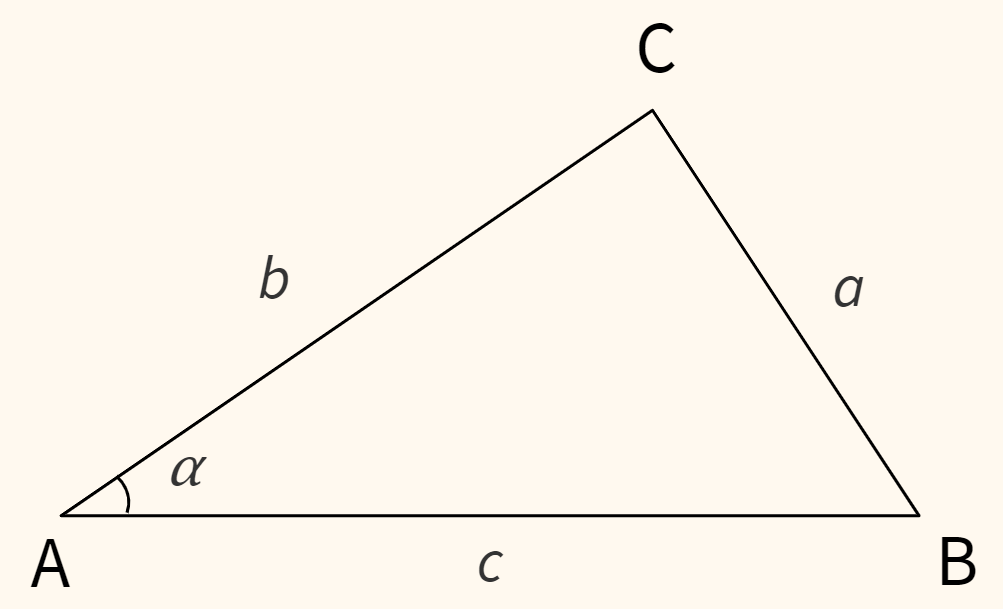
По теореме косинусов

$$ a^2 = b^2 + c^2-2bc \cdot \cos \alpha $$

$$ \cos \alpha = \frac{ b^2 + c^2-a^2 }{2bc} $$

$$ \alpha = \arccos \left( \frac{ b^2 + c^2-a^2 }{2bc} \right) $$

Приведем несложное доказательство. Вначале из вершины $C$ на сторону $AB$ опустим высоту $CD$.

Рассмотрим треугольник $ADC$ и выразим сторону $AD$ через косинус угла $\alpha$.

$$ \cos \alpha = \frac{AD}{b}, \quad AD = b \cdot \cos \alpha $$

Следовательно,

$$ DB = c-b \cdot \cos \alpha $$

По теореме Пифагора найдем, чему равна сторона $h$ в прямоугольных треугольниках $ADC$ и $BDC$.

$$ h^2 = b^2-(b \cdot \cos \alpha)^2 $$

$$ h^2 = a^2-(c-b \cdot \cos \alpha)^2 $$

Приравняем правые части уравнений.

$$ b^2-(b \cdot \cos \alpha)^2 = a^2-(c-b \cdot \cos \alpha)^2 $$

$$ a^2 = b^2 + c^2-2bc \cdot \cos \alpha $$

Косинусное сходство

Теперь представим стороны треугольника в виде векторов.

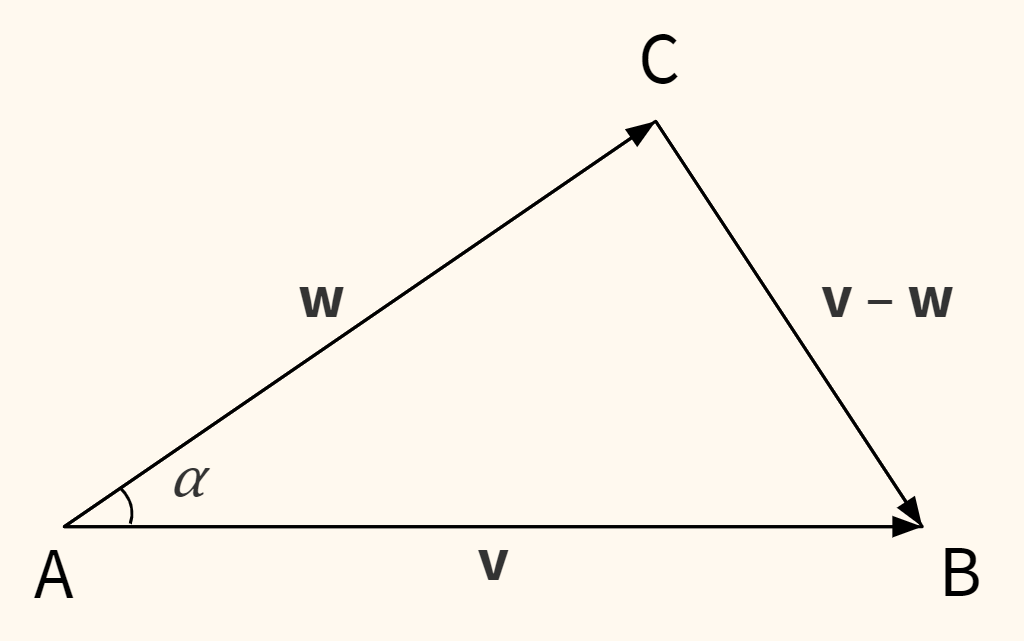
Пока примем без доказательства, что сторона $CD$ является разностью векторов $\mathbf v$ и $\mathbf{w}.$ Тогда из теоремы косинусов (опять же мы докажем это позднее) можно вывести формулу скалярного произведения как произведения длин векторов любой размерности на косинус угла между ними

$$ \mathbf w \cdot \mathbf v = || \mathbf w || \cdot || \mathbf v || \cdot \cos \alpha $$

и, как следствие, косинусного сходства между этими векторами

$$ \cos \alpha = \frac{\mathbf w \cdot \mathbf v}{|| \mathbf w || \cdot || \mathbf v ||} $$

Проверим с помощью косинусного сходства угол между приведенными выше двумерными векторами, а также ещё раз разберём уже знакомый пример трехмерных векторов.

Двумерные векторы

Ещё раз приведем исходные векторы.

$$ \textbf{v} = \begin{bmatrix} \frac{ \sqrt{2} } {2} \\ \frac{ \sqrt{2} } {2} \end{bmatrix}, \quad \textbf{w} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} $$

Так как векторы единичной длины, т.е. $|| \mathbf w || = || \mathbf v || = 1$, то косинус угла просто равен скалярному произведению этих векторов.

$$ \cos \alpha = \mathbf w \cdot \mathbf v = \frac{ \sqrt{2} } {2} \cdot 1 + \frac{ \sqrt{2} } {2} \cdot 0 = \frac{ \sqrt{2} } {2} $$

$$ \alpha = \arccos \frac{ \sqrt{2} } {2} = \frac{\pi}{4} \text{ rad} = 45^{\circ} $$

Многомерные векторы

Теперь вернемся к примеру, рассмотренному в рамках вводного курса, и выполним его заново. Напомню, нам были даны два трехмерных вектора.

$$ \mathbf b = \begin{bmatrix} 1,72 \\ 54 \\ 36,2 \end{bmatrix}, \quad \mathbf c = \begin{bmatrix} 1,56 \\ 47 \\ 30 \end{bmatrix} $$

Параллельно будем проверять себя с помощью Питона.

Откроем ноутбук к этому занятию⧉

Еще раз приведем рабочую формулу.

$$ \cos \theta = \frac{\mathbf b \cdot \mathbf c}{|| \mathbf b || \cdot || \mathbf c ||} $$

Вначале вычислим скалярное произведение векторов.

$$ \mathbf b \cdot \mathbf c = 1,72 \times 1,56 + 54 \times 47 +36,2 \times 30 \approx 3626,6832 $$

Теперь найдем длину или L2 норму каждого из векторов.

$$ || \mathbf b || = \sqrt{x_1^2 + x_2^2 + x_3^2} = \sqrt{1,72^2 + 54^2 + 36,2^2} \approx 65,03 $$

$$ || \mathbf c || = \sqrt{1,56^2 + 47^2 + 30^2} \approx 55,78 $$

Перемножим длины векторов.

$$ 65,03 \times 55,78 \approx 3627 $$

Далее найдем косинус угла $\theta$.

$$ \cos \theta = \frac{3626}{3627} \approx 0,9997 $$

Остается найти угол $\theta$. Вначале найдем угол в радианах с помощью функции np.arccos().

Наконец, для целей практики, найдем приближенное значение угла в градусах, а затем сделаем более точное вычисление с помощью Питона. Итак,

$$ \frac{225}{10 000} \text{ rad} = \frac{225}{10 000} \times \frac{180}{\pi} \approx 1,3^{\circ} $$

Промежуточный итог

Выше мы показали, как перейти от понятия синуса, косинуса и тангенса к измерению углов на окружности, углов прямоугольного и наконец любого плоского треугольника.

После этого мы перешли от измерения угла, образованного сторонами треугольника, к углу между векторами, более подробно разобрав формулу косинусного сходства и пример из вводного курса.

На курсе линейной алгебры мы продолжим знакомиться с векторами и операциями над ними.