Векторы

Все курсы > Линейная алгебра > Занятие 1

На первом занятии мы более подробно рассмотрим понятие вектора.

Ноутбук к сегодняшнему занятию⧉

Понятие вектора

Вектор (vector) — это направленный отрезок, и для нас будет важно, что любой вектор обладает длиной (magnitude) и направлением (direction).

На курсе мы будем обозначать векторы полужирной строчной буквой, например $\textbf{a}$, а матрицы заглавной буквой, например, А.

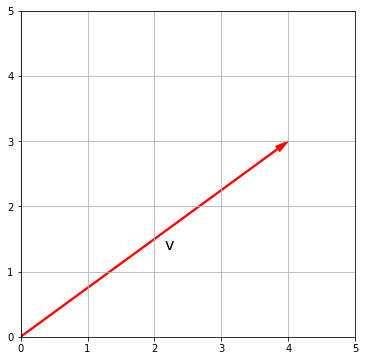
Возьмём двумерный вектор $\textbf{v}$

$$ \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix} $$

Вектор $\textbf{v}$ удобно изобразить на координатной плоскости, исходящим из начала координат.

Добавлю, что вектор — частный случай матрицы. В случае вектор-столбца речь идет о матрице размерностью n x 1. В случае вектор-строки — 1 x n. Вектор $\textbf{v}$ — это матрица 2 х 1.

Операции над векторами

Сложение векторов

Складывать векторы очень несложно. Достаточно сложить их компоненты или координаты.

$$ \begin{bmatrix} 4 \\ 3 \end{bmatrix} + \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 6 \\ 2 \end{bmatrix} $$

Графически, если поставить начало второго вектора в конец первого, сложение можно представить как расстояние от начала первого вектора до конца второго. Своего рода путь, пройденный двумя векторами.

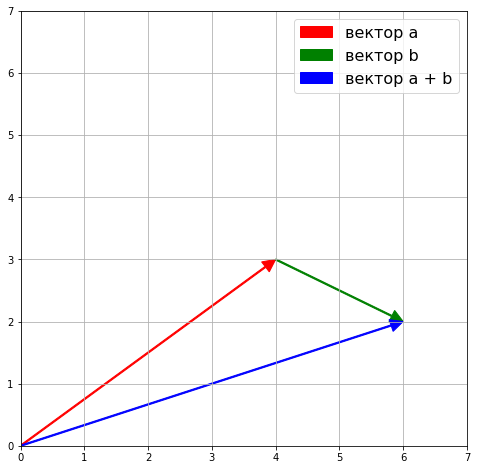
Сложение векторов ассоциативно $\textbf{a} + \textbf{b} = \textbf{b} + \textbf{a}$.

Умножение на скаляр

Умножение на скаляр просто удлиняет или укорачивает вектор.

$$ 2 \cdot \textbf{v} = 2 \cdot \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} 8 \\ 6 \end{bmatrix} $$

Умножение на отрицательное число не только удлиняет или укорачивает вектор, но и переворачивает его направление.

$$ -0,5 \cdot \textbf{v} = -0,5 \cdot \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ -1,5 \end{bmatrix} $$

Очевидно, что умножение на −1 просто переворачивает направление вектора, но не меняет его длины.

$$ -1 \cdot \textbf{v} = -1 \cdot \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} -4 \\ -3 \end{bmatrix} $$

Вычитание и деление на число

Вычитание векторов можно представить как сумму первого вектора со вторым вектором, умноженным на −1.

$$ \begin{bmatrix} 4 \\ 3 \end{bmatrix} + \left( -1 \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} \right) = \begin{bmatrix} 2 \\ 4 \end{bmatrix} $$

Графически мы сначала находим вектор $\textbf{-b}$ (зеленая стрелка), а затем прибавляем его к вектору $\textbf{a}$ (красная стрелка).

Остается добавить, что деление вектора на число, это всего лишь умножение на обратное число (multiplicative inverse). Разделим вектор $\textbf{v}$ на семь.

$$ \frac{\textbf{v}}{7} = \begin{bmatrix} 4 \\ 3 \end{bmatrix} \cdot \frac{1}{7} = \begin{bmatrix} \frac{4}{7} \\ \frac{3}{7} \end{bmatrix} $$

Тот факт, что мы выразили вычитание через сложение и умножение на скаляр, а деление через умножение на обратное число позволило нам остаться в пределах операций сложения и умножения на скаляр.

Видео про векторы⧉.

Длина вектора

Длину или норму вектора (norm, length, magnitude or size of a vector) рассчитать не сложно, достаточно вспомнить теорему Пифагора. Снова возьмем вектор $\textbf{v}$

$$ \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix} $$

Как видно на графике, вектор $\textbf{v}$, смещение вдоль оси x и смещение вдоль оси y образуют прямоугольный треугольник. Значит, длина вектора (гипотенуза) равна квадратному корню из суммы квадратов смещений (катетов или в нашем случае координат).

$$ ||\textbf{v}|| = \sqrt{4^2 + 3^2} = \sqrt{25} = 5 $$

Для n-мерного вектора ничего не меняется.

$$ ||\textbf{v}|| = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2} $$

Например, найдем длину трехмерного вектора $\textbf{w}$.

$$ \textbf{w} = \begin{bmatrix} 6 \\ 3 \\ 2 \end{bmatrix} \rightarrow ||\textbf{w}|| = \sqrt{6^2 + 3^2 + 2^2} = \sqrt{49} = 7 $$

Единичный вектор

Вектор с длиной, равной единице, называют единичным вектором (unit vector). Примерами единичных векторов, с которыми мы будем часто встречаться в пространстве $ R^2 $, являются следующие два вектора

$$ \hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $$

Единичный вектор принято обозначать строчной буквой с знаком циркумфлекса, «крышечки» (hat).

Проверим, равна ли их длина единице.

$$ ||\hat{i}|| = \sqrt{1^2 + 0^2} = \sqrt{1} = 1, ||\hat{j}|| = \sqrt{0^2 + 1^2} = \sqrt{1} = 1 $$

Интересно, что с помощью векторов $ \hat{i}, \hat{j} $ можно выразить любой другой вектор в $ R^2 $. Например, вектор $\textbf{v}$ можно представить как

$$ 4 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 3 \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 3 \end{bmatrix} \rightarrow 4\hat{i} + 3 \hat{j} $$

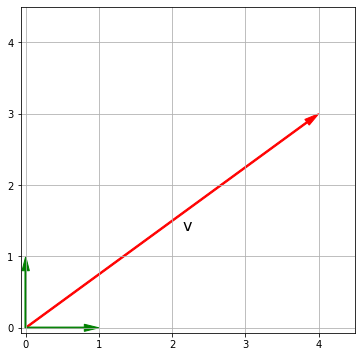
Это обстоятельство нам пригодится в будущем.

Нормализация вектора

Длина нормализованного вектора равна единице. Для того чтобы нормализовать вектор, достаточно разделить вектор на его длину. Создадим единичный вектор $\hat{v}$ для вектора $\textbf{v}$.

$$ \hat{v} = \frac{\textbf{v}}{||\textbf{v}||} = \frac{1}{5} \cdot \begin{bmatrix} 4 \\ 3 \end{bmatrix} = \begin{bmatrix} \frac{4}{5} \\ \frac{3}{5} \end{bmatrix} $$

Скалярное произведение

Важной операцией над векторами является уже знакомое нам скалярное произведение (dot product). В качестве напоминания того, как работает скалярное произведение приведем несложный пример. Пусть даны два вектора $\textbf{v}$ и $\textbf{w}$.

$$ \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}, \textbf{w} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} $$

Найдем их скалярное произведение.

$$ \textbf{v} \cdot \textbf{w} = 4 \cdot 2 + 3 \cdot 1 = 11 $$

Как вы видите, мы перемножаем компоненты векторов и складываем получившиеся произведения.

Скалярное произведение как длина вектора

Интересно, что корень из скалярного произведения вектора на самого себя есть его длина.

$$ \sqrt{ \textbf{v} \cdot \textbf{v} } = \sqrt{4 \cdot 4 + 3 \cdot 3 } = \sqrt{ 4^2 + 3^2 } = \sqrt{25} = 5 $$

Угол между векторами

В предисловии мы сказали, что скалярное произведение также определяется как произведение длин векторов на косинус угла между ними.

$$ \mathbf a \cdot \mathbf b = || \mathbf a || \cdot || \mathbf b || \cdot \cos \theta $$

Именно это свойство привело нас к расчету косинусного сходства между векторами.

$$ \cos \theta = \frac{\mathbf a \cdot \mathbf b}{|| \mathbf a || \cdot || \mathbf b ||} $$

Выведем эту формулу. Вначале вспомним теорему косинусов.

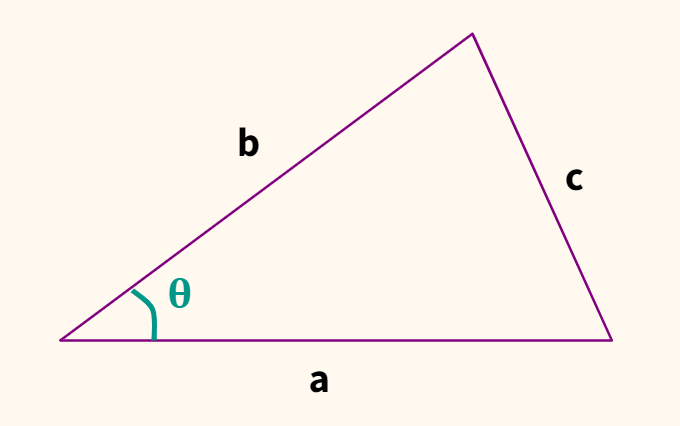
$$ c^2 = a^2 + b^2-2ab \cdot \cos \theta $$

Теперь представим, что у нас не стороны треугольника, а векторы. Если сторону а обозначить как вектор $ \textbf{a} $, сторону b — как вектор $ \textbf{b} $, то сторона с станет разностью между $ \textbf{a} $ и $ \textbf{b} $ (чтобы убедиться в этом, найдите $ \textbf{-b} $ и приставьте его к окончанию $ \textbf{a} $).

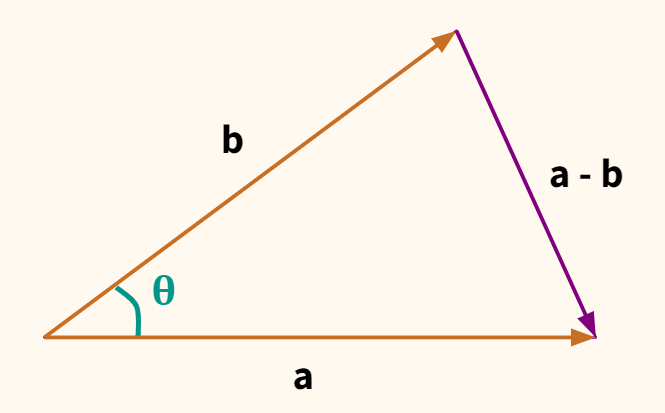
Выразим теорему косинусов через длины векторов. Другими словами, представим, что мы имеем дело не с отрезками на плоскости, а с многомерными векторами (для удобства не будем выделять векторы полужирным шрифтом).

$$ || a-b ||^2 = ||a||^2 + ||b||^2-2 \cdot ||a|| \cdot ||b|| \cdot \cos \theta $$

Помня, что длина есть скалярное произведение вектора на самого себя, мы можем выразить левую часть $ || a-b || $ как

$$ (a-b)(a-b) = a \cdot a-a \cdot b-b \cdot a + (-b) \cdot (-b) = ||a||^2-2ab + ||b||^2 $$

Поместим результат в исходное выражение.

$$ ||a||^2-2ab + ||b||^2 = ||a||^2 + ||b||^2-2 \cdot ||a|| \cdot ||b|| \cdot \cos \theta $$

Сократив подобные члены получим

$$ a \cdot b = ||a|| \cdot ||b|| \cdot \cos \theta $$

Выводы. Из тригонометрии мы помним, что косинус 90 градусов равен нулю. Как следствие, скалярное произведение перпендиклярных (правильнее сказать ортогональных (orthogonal)) векторов $ \textbf{a} \perp \textbf{b} $ равно нулю.

$$ a \cdot b = ||a|| \cdot ||b|| \cdot \cos 90^{\circ} = 0 $$

Очевидно, что если угол между двумерными векторами меньше 90 градусов, косинус, а значит и скалярное произведение положительны. В противном случае — отрицательны. Для n-мерных векторов положительное скалярное произведение говорит, что они в целом смотрят в одну строну, отрицательное — противоположные.

Для коллинеарных (сонаправленных) векторов скалярное произведение равно произведению их длин, потому что косинус нуля равен единице.

$$ a \cdot b = ||a|| \cdot ||b|| \cdot \cos 0^{\circ} = ||a|| \cdot ||b|| $$

Добавлю, что если $ \textbf{a} $ и $ \textbf{b} $ — единичные векторы, то косинус угла между векторами просто равен его их скалярному произведению.

$$ \cos \theta = a \cdot b $$

Рассчитаем косинусное расстояние для векторов

$$ \textbf{v} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}, \textbf{w} = \begin{bmatrix} 1 \\ 7 \end{bmatrix} $$

Внешнее произведение

Под внешним произведением (outer product) понимается умножение вектор-столбца на вектор-строку по обычным правилам матричного умножения. Результатом такого произведения будет матрица, а не число, как в случае скалярного произведения.

Ортогональность векторов

Еще раз продемонстрируем, почему если векторы ортогональны, их скалярное произведение будет равно нулю. Возьмем три вектора, образовывающих прямоугольный треугольник.

Тогда, по теореме Пифагора,

$$ || \mathbf x ||^2 + || \mathbf y ||^2 = || \mathbf x + \mathbf y ||^2 $$

$$ \mathbf x^T \mathbf x + \mathbf y^T \mathbf y = (\mathbf x + \mathbf y)^T (\mathbf x + \mathbf y) $$

$$ \mathbf x^T \mathbf x + \mathbf y^T \mathbf y = \mathbf x^T \mathbf x + \mathbf y^T \mathbf y + \mathbf x^T \mathbf y + \mathbf y^T \mathbf x $$

$$ \mathbf x^T \mathbf x + \mathbf y^T \mathbf y = \mathbf x^T \mathbf x + \mathbf y^T \mathbf y + 2 \mathbf x^T \mathbf y $$

$$ \mathbf 0 = 2 \mathbf x^T \mathbf y $$

$$ \mathbf x^T \mathbf y = \mathbf 0 $$

Проекция вектора на вектор

Подойдем к скалярному произведению с другой стороны. Рассмотрим два вектора $ \textbf{a} $ и $ \textbf{b} $ и найдем проекцию первого вектора на второй.

Проекция через угол между векторами

Говоря неформально, проекцией вектора $ \textbf{a} $ на вектор $ \textbf{b} $ будет такой участок вектора $ \textbf{b} $, что расстояние от точки A до точки B минимально. Минимальным оно будет, если угол OAB будет равен 90 градусов. Получается прямоугольный треугольник. Найдем отрезок OB.

$$ \cos \theta = \frac {OB}{OA} = \frac {OB}{|| \mathbf a ||} \rightarrow OB = || \mathbf a || \cdot \cos \theta $$

Выразим то же самое через формулу скалярного произведения, заменив $|| \mathbf a || \cdot \cos \theta $ на OB.

$$ \mathbf b \cdot \mathbf a = || \mathbf b || \cdot || \mathbf a || \cdot \cos \theta \rightarrow \mathbf b \cdot \mathbf a = || \mathbf b || \cdot OB $$

Так мы нашли длину проекции OB. Ее называют числовой или скалярной проекцией (scalar projection).

$$ \frac{\mathbf b \cdot \mathbf a}{|| \mathbf b ||} = || \mathbf a || \cdot \cos \theta = OB $$

Более того, если длина вектора $ \textbf{b} $ равна единице, то длина проекции OB просто равна скалярному произведению.

$$ || \mathbf b || = 1 \rightarrow \mathbf b \cdot \mathbf a = OB $$

Это объясняет, почему скалярное произведение еще называют projection product.

Очевидное и тем не менее интересное примечание. Обратите внимание на связь понимания скалярного произведения как проекции одного вектора на другой и произведения длин векторов на косинус угла между ними. Если векторы перпендикулярны, проекция одного вектора на другой равна нулю, а значит и произведение проекции второго вектора на первый равно нулю.

Предположим, нас интересует не только длина проекции, но и ее направление. В этом случае говорят про векторную проекцию (vector projection).

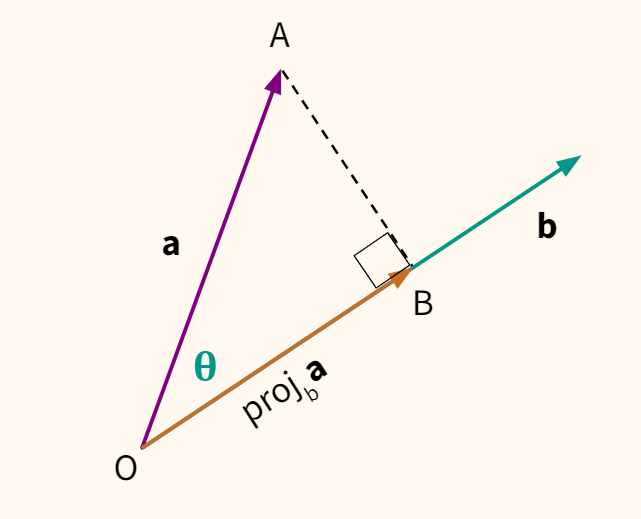
Она выражается как произведение нормализованного вектора $ \textbf{b} $ на длину проекции (то есть скалярную проекцию) OB.

$$ proj_\mathbf{b} \textbf{a} = OB \cdot \hat{b} $$

Перепишем OB через скалярное произведение, а $\hat{b}$ через частное вектора $ \textbf{b} $ на его длину.

$$ proj_\mathbf{b} \textbf{a} = \frac{\mathbf b \cdot \mathbf a}{|| \mathbf b ||} \cdot \frac{\mathbf b}{|| \mathbf b ||} $$

Таким образом, можно сказать, что векторная проекция показывает, длину вектора $ \textbf{a} $ в направлении вектора $ \textbf{b} $.

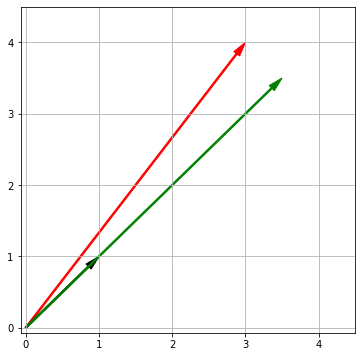
Пример. Возьмем два вектора $ \mathbf a$ и $ \mathbf b$ и найдем вначале скалярную, затем векторную проекцию вектора $ \mathbf a$ на вектор $ \mathbf b$.

Матрица проекции

Векторную проекцию можно выразить с помощью матрицы проекции $P$.

$$ proj_\mathbf{b} \textbf{a} = P \cdot \mathbf a = \frac{\mathbf b \mathbf b^T}{\mathbf b^T \mathbf b} \cdot \mathbf a $$

В знаменателе находится скалярное произведение и результатом умножения будет число. В числителе — внешнее произведение и результатом будет матрица. Найдем внешнее произведение из примера выше.

Найдем скалярное произведение.

Создадим матрицу проекции $P$ и умножим ее на вектор $\mathbf a$.

Симметрия скалярного произведения

Продемонстрируем с точки зрения проекции, почему $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a $. Возьмем два вектора $\mathbf a$ и $\mathbf b$.

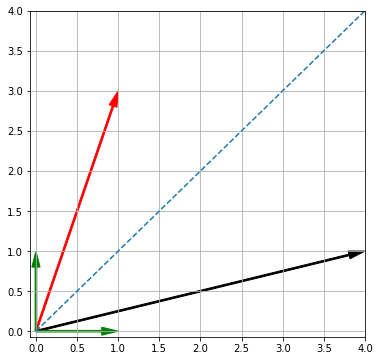
Выше мы сказали, что $ \mathbf a \cdot \mathbf b = OB \cdot || \mathbf b|| $. То есть скалярное произведение вектора $\mathbf a$ на вектор $\mathbf b$ равно произведению проекции $\mathbf a$ на $\mathbf b$, умноженной на длину вектора $\mathbf b$.

Продемонстрируем, что произведение проекции вектора $\mathbf a$ на вектор $\mathbf b$, умноженное на длину вектора $\mathbf b$, равно произведению проекции вектора $\mathbf b$ на вектор $\mathbf a$, умноженному на длину вектора $\mathbf a$.

$$ proj_b \mathbf a \times || \mathbf b || = proj_a \mathbf b \times || \mathbf a || $$

Видео про скалярное произведение векторов⧉.

Векторное произведение

Векторное произведение (cross product) задано только в трехмерном пространстве. Результатом такого произведения будет вектор, перпендикулярный каждому из исходных векторов. Приведем иллюстрацию из Википедии⧉.

Математически векторное произведение задается формулой

$$ \mathbf a \times \mathbf b = || \mathbf a || \cdot || \mathbf b || \cdot \sin \theta $$

Геометрически — это площадь параллелограмма, сформированного из исходных векторов $\mathbf a$ и $\mathbf b$.

Приведем пример.

Подведем итог

Сегодня мы ввели понятие вектора, познакомились с базовыми операциями с векторами, в частности, изучили скалярное произведение векторов и научились находить скалярную и векторную проекцию одного вектора на другой.

Перейдем к рассмотрению векторного пространства.