Преобразование данных. Часть 1 | Анализ и обработка данных

Все курсы > Анализ и обработка данных > Занятие 8 (часть 1)

Для многих моделей машинного обучения важно, чтобы количественные данные имели одинаковый масштаб (same scale). Это справедливо для

алгоритмов, рассчитывающих расстояние (например, алгоритм k-ближайших соседей или метод k-средних), а также
моделей, оптимизирующих веса методом градиентного спуска и использующих регуляризацию (в частности, это линейная или логистическая регрессия).

Кроме того, в некоторых случаях нам может понадобиться преобразовать данные так, чтобы привести их к распределению, более похожему на нормальное. Это может быть важно для

проведения статистических тестов
превращения нелинейной зависимости в линейную (что важно, в частности, для вычисления линейной корреляции или использования линейной модели)
стабилизации дисперсии, например, при выявлении гетероскедастичности остатков модели линейной регрессии

Сегодняшнее занятие в большей степени посвящено способам и инструментам преобразования данных и выявления выбросов. Практикой их применения мы займемся на последующих занятиях.

Содержание занятия

Откроем ноутбук к этому занятию⧉

Подготовка данных

Скачаем и подгрузим данные о недвижимости в Бостоне.

boston.csv Скачать

Подготовим данные.

# возьмем признак LSTAT (процент населения с низким социальным статусом)

# и целевую переменную MEDV (медианная стоимость жилья)

boston = pd.read_csv('/content/boston.csv')[['LSTAT', 'MEDV']]

boston.shape

(506, 2)

Визуализируем распределения с помощью гистограммы.

1	boston.hist(bins = 15, figsize = (10, 5));

преобразование количественных переменных, датасет о недвижимости в Бостоне

Посмотрим на основные статистические показатели.

1	boston.describe()

метод .describe(), датасет о недвижимости в Бостоне

Линейные и нелинейные преобразования

Ключевое отличие масштабирования от приближения одного распределения к другому, например, нормальному распределению (а именно эти два типа преобразования мы в основном будем рассматривать на сегодняшнем занятии), заключается в том, что первая трансформация линейна, вторая — нелинейна.

Линейные преобразования (linear transformation) не меняют структуру распределения, нелинейные преобразования (non-linear transformation) — меняют.

Возьмем скошенное вправо распределение LSTAT и применим к нему один из способов масштабирования, стандартизацию, и нелинейное преобразование Бокса-Кокса (смысл этих преобразований мы подробно рассмотрим ниже).

# создадим сетку подграфиков 1 x 3

fig, ax = plt.subplots(nrows = 1, ncols = 3, figsize = (12,4))

# на первом графике разместим изначальное распределение

sns.histplot(data = boston, x = 'LSTAT',

bins = 15,

ax = ax[0])

ax[0].set_title('Изначальное распределение')

# на втором - данные после стандартизации

sns.histplot(x = (boston.LSTAT - np.mean(boston.LSTAT)) / np.std(boston.LSTAT),

bins = 15, color = 'green',

ax = ax[1])

ax[1].set_title('Стандартизация')

# наконец скачаем функцию степенного преобразования power_transform()

from sklearn.preprocessing import power_transform

# и на третьем графике покажем преобразование Бокса-Кокса

sns.histplot(x = power_transform(boston[['LSTAT']],

method = 'box-cox').flatten(),

bins = 12, color = 'orange',

ax = ax[2])

ax[2].set(title = 'Степенное преобразование', xlabel = 'LSTAT')

plt.tight_layout()

plt.show()

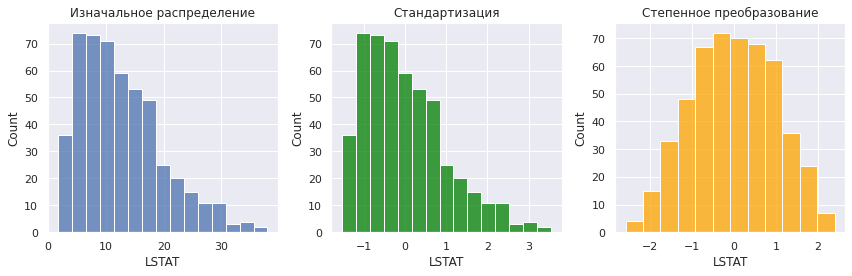
пример стандартизации и степенного преобразования

Как вы видите, в первом случае скошенность (skewness) и в целом форма распределения сохранилась, изменился только масштаб (среднее значение сместилось к нулю, изменился разброс). Во втором случае, изменилась сама структура распределения, то есть соотношение расстояний между точками.

Замечу, что в основном сегодня мы будем пользоваться модулем preprocessing⧉ библиотеки sklearn или трансформационными инструментами⧉ Scipy.

Добавление выбросов

Как уже было сказано выше, выбросы очень сильно влияют на качество данных. Для того чтобы посмотреть, как рассматриемые нами инструменты справляются с выбросами, добавим несколько сильно отличающихся от общей массы наблюдений.

# сделаем копию датафрейма

boston_outlier = boston.copy()

# создадим два отличающихся наблюдения

outliers = [pd.Series([45, 70], index = boston_outlier.columns),

pd.Series([50, 72], index = boston_outlier.columns)]

# добавим их в датафрейм

boston_outlier = boston_outlier.append(outliers, ignore_index = True)

# посмотрим на размерность нового датафрейма

boston_outlier.shape

(508, 2)

1 2	# убедимся, что наблюдения добавились boston_outlier.tail()

Посмотрим на данные с выбросами и без.

fig, ax = plt.subplots(1, 2, figsize = (12,6))

sns.scatterplot(data = boston, x = 'LSTAT', y = 'MEDV', ax = ax[0]).set(title = 'Без выбросов')

sns.scatterplot(data = boston_outlier, x = 'LSTAT', y = 'MEDV', ax = ax[1]).set(title = 'С выбросами');

точечная диаграмма: данные с выбросами и без

Линейные преобразования (масштабирование)

Рассмотрим несколько способов масштабирования признаков (feature scaling).

Стандартизация

Если данные имеют нормальное или близкое к нормальному распределение (что желательно для многих моделей ML), имеет смысл прибегнуть к стандартизации (standartazation): то есть приведению к нулевому среднему значению и единичному СКО (так называемое стандартное нормальное распределение). Приведем формулу.

$$ x’ = \frac{x-\mu}{\sigma} $$

На практике стандартизация оказывается полезна и в тех случаях, когда данные не следуют нормальному распределению.

Стандартизация вручную

Замечу, что часто бывает удобно стандартизировать данные без использования класса sklearn.

1	((boston - np.mean(boston)) / np.std(boston)).head(3)

StandardScaler

Преобразование данных

Точно такой же результат можно получить через класс StandardScaler модуля preprocessing библиотеки sklearn. Создадим объект этого класса и применим метод .fit().

# из модуля preprocessing импортируем класс StandardScaler

from sklearn.preprocessing import StandardScaler

# создадим объект класса StandardScaler и применим метод .fit()

st_scaler = StandardScaler().fit(boston)

st_scaler

1	StandardScaler()

При вызове метода .fit() алгоритм рассчитывает среднее арифметическое и СКО каждого из столбцов. Их можно посмотреть через соответствующие атрибуты.

1 2	# выведем среднее арифметическое st_scaler.mean_

1	array([12.65306324, 22.53280632])

1 2	# и СКО каждого из столбцов array([7.13400164, 9.18801155])

Метод .transform() соответственно использует рассчитанные значения среднего и СКО для стандартизации данных.

# метод .transform() возвращает массив Numpy с преобразованными значениями

boston_scaled = st_scaler.transform(boston)

# превратим массив в датафрейм с помощью функции pd.DataFrame()

pd.DataFrame(boston_scaled, columns = boston.columns).head(3)

Метод .fit_transform() сразу вычисляет статистические показатели и применяет их для масштабирования данных.

1 2	boston_scaled = pd.DataFrame(StandardScaler().fit_transform(boston), columns = boston.columns)

# аналогичным образом стандиртизируем данные с выбросами

boston_outlier_scaled = pd.DataFrame(StandardScaler().fit_transform(boston_outlier),

columns = boston_outlier.columns)

Визуализация преобразования

Объявим две вспомогательные функции, которые помогут нам визуализировать эту и ряд последующих трансформаций для данных с выбросами и без. Первая фунция будет выводить точечные диаграммы.

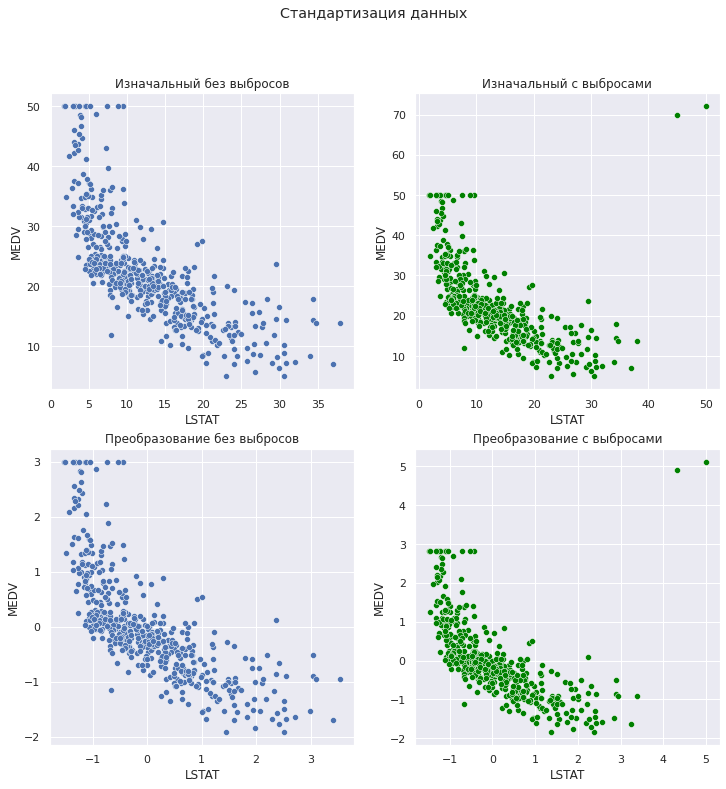
# первая функция будет принимать на вход четыре датафрейма

# и визуализировать изменения с помощью точечной диаграммы

def scatter_plots(df, df_outlier, df_scaled, df_outlier_scaled, title):

fig, ax = plt.subplots(2, 2, figsize = (12,12))

sns.scatterplot(data = df, x = 'LSTAT', y = 'MEDV', ax = ax[0, 0])

ax[0, 0].set_title('Изначальный без выбросов')

sns.scatterplot(data = df_outlier, x = 'LSTAT', y = 'MEDV', color = 'green', ax = ax[0, 1])

ax[0, 1].set_title('Изначальный с выбросами')

sns.scatterplot(data = df_scaled, x = 'LSTAT', y = 'MEDV', ax = ax[1, 0])

ax[1, 0].set_title('Преобразование без выбросов')

sns.scatterplot(data = df_outlier_scaled, x = 'LSTAT', y = 'MEDV', color = 'green', ax = ax[1, 1])

ax[1, 1].set_title('Преобразование с выбросами')

plt.suptitle(title)

plt.show()

# вторая функция будет визуализировать изменения с помощью гистограммы

def hist_plots(df, df_outlier, df_scaled, df_outlier_scaled, title):

fig, ax = plt.subplots(2, 2, figsize = (12,12))

sns.histplot(data = df, x = 'LSTAT', ax = ax[0, 0])

ax[0, 0].set_title('Изначальный без выбросов')

sns.histplot(data = df_outlier, x = 'LSTAT', color = 'green', ax = ax[0, 1])

ax[0, 1].set_title('Изначальный с выбросами')

sns.histplot(data = df_scaled, x = 'LSTAT', ax = ax[1, 0])

ax[1, 0].set_title('Преобразование без выбросов')

sns.histplot(data = df_outlier_scaled, x = 'LSTAT', color = 'green', ax = ax[1, 1])

ax[1, 1].set_title('Преобразование с выбросами')

plt.suptitle(title)

plt.show()

Применим эти функции к стандартизированным данным.

scatter_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'Стандартизация данных')

точечная диаграмма: стандартизация данных с выбросами и без

hist_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'Стандартизация данных')

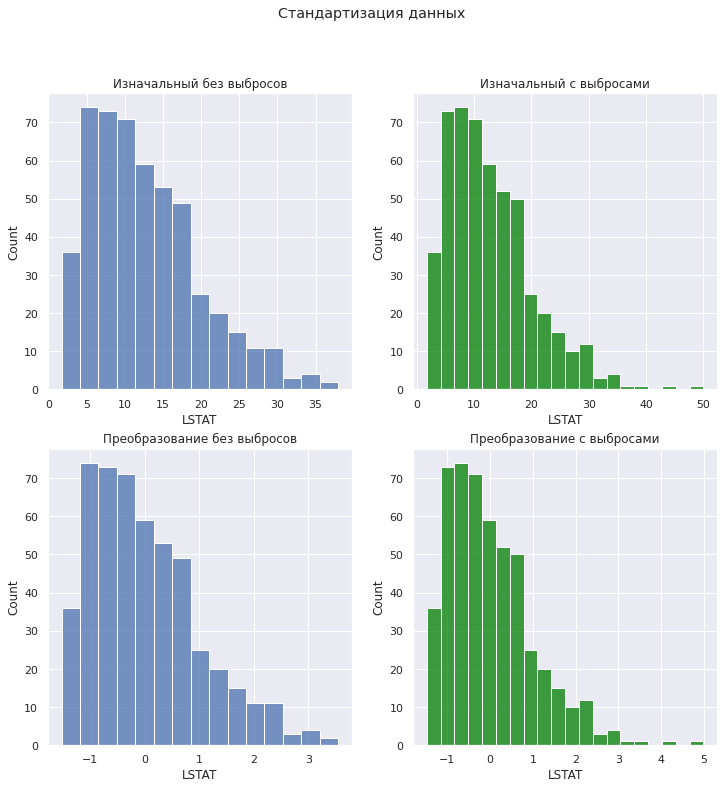
Обратите внимание, что стандартизация не ограничивает данные определенным диапазоном и допускает отрицательные значения. Кроме того, этот метод чувствителен к выбросам в том смысле, что влияет на расчет СКО, и диапазон двух признаков с выбросами после стандартизации все равно будет различаться.

Как следствие, при наличии выбросов стандартизация не гарантирует одинаковый масштаб признаков.

Хорошая иллюстрация этого факта есть на сайте библиотеки sklearn⧉.

Обратное преобразование

Вернуть исходный масштаб можно с помощью метода .inverse_transform().

1 2	boston_inverse = pd.DataFrame(st_scaler.inverse_transform(boston_scaled), columns = boston.columns)

Иногда возникает вопрос, почему исходные и преобразованные к исходному виду данные не будут идентичными.

1 2	# используем метод .equals(), чтобы выяснить, одинаковы ли датафреймы boston.equals(boston_inverse)

False

Это связано лишь с особенностями округления (как видно ниже различия минимальны).

1 2	# вычтем значения одного датафрейма из значений другого (boston - boston_inverse).head(3)

обратное преобразование после стандартизации

Одновременно не всегда бывает понятно, зачем использовать класс StandardScaler, когда быстрее написать код самостоятельно.

Проблема утечки данных

В ответах на вопросы к занятию по классификации (в рамках вводного курса), мы уже поднимали вопрос применения стандартизации к обучающей и тестовой выборкам и упомянули проблему утечки данных (data leakage). Рассмотрим этот вопрос еще раз.

Если мы сразу отмасштабируем все данные (и обучающую, и тестовую выборки), то информация из тестовой части «утечет» в обучающую просто потому, что, в случае стандартизации, среднее и СКО будет рассчитываться на основе всех данных. Как следствие, модель на этапе обучения уже «увидит» тестовые данные, а значит качество модели «на тесте» может быть неоправданно завышено.

Для того чтобы тестовые данные никак не влияли на обучающую часть, нужно:

рассчитать среднее и СКО обучающей выборки
отмасштабировать обучающие данные
обучить на них модель
использовать ранее рассчитанные среднее и СКО для масштабирования тестовых данных
сделать прогноз на отмасштабированных тестовых данных и оценить качество модели

Именно такое разделение и обеспечивают методы .fit() и .transform().

Перейдем к практике.

# импортируем данные о недвижимости в Калифорнии

from sklearn.datasets import fetch_california_housing

# при return_X_y = True вместо объекта Bunch возвращаются признаки (X) и целевая переменная (y)

# параметр as_frame = True возвращает датафрейм и Series вместо массивов Numpy

X, y = fetch_california_housing(return_X_y = True, as_frame = True)

# убедимся, что данные в нужном нам формате

type(X), type(y)

1	(pandas.core.frame.DataFrame, pandas.core.series.Series)

1 2	# посмотрим на признаки X.head(3)

# разделим данные на обучающую и тестовую выборки

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y,

random_state = 42)

# импортируем класс для стандартизации данных

from sklearn.preprocessing import StandardScaler

# и создания модели линейной регрессии

from sklearn.linear_model import LinearRegression

# создадим объект класса StandardScaler

scaler = StandardScaler()

scaler

1	StandardScaler()

# масштабируем признаки обучающей выборки

X_train_scaled = scaler.fit_transform(X_train)

# убедимся, что объект scaler запомнил значения среднего и СКО

# для каждого признака

scaler.mean_, scaler.scale_

(array([ 3.87831412e+00, 2.85959948e+01, 5.43559839e+00, 1.09688116e+00,

1.42749729e+03, 3.10665968e+00, 3.56467196e+01, -1.19583736e+02]),

array([1.90372658e+00, 1.26109222e+01, 2.42157219e+00, 4.38789636e-01,

1.14289394e+03, 1.19554480e+01, 2.13388067e+00, 2.00237697e+00]))

# применим масштабированные данные для обучения модели линейной регрессии

model = LinearRegression().fit(X_train_scaled, y_train)

model

1	LinearRegression()

# преобразуем тестовые данные с использованием среднего и СКО, рассчитанных на обучающей выборке

# так тестовые данные не повляют на обучение модели, и мы избежим утечки данных

X_test_scaled = scaler.transform(X_test)

# сделаем прогноз на стандартизированных тестовых данных

y_pred = model.predict(X_test_scaled)

y_pred[:5]

1	array([0.72412832, 1.76677807, 2.71151581, 2.83601179, 2.603755 ])

1 2	# и оценим R-квадрат (метрика (score) по умолчанию для класса LinearRegression) model.score(X_test_scaled, y_test)

1	0.5910509795491352

Применение пайплайна

По мере увеличения количества этапов работы с данными, количество кода также увеличилось. Сделать запись более экономной можно с помощью пайплайна.

Пайплайн (pipeline) последовательно применяет заданные преобразования данных (transformer) и выдает прогноз или метрику последнего по порядку инструмента, как правило, класса модели (estimator).

В нашем случае инструмента два: StandardScaler (transformer) и LinearRegression (estimator). Вначале рассмотрим более простой с точки зрения синтаксиса способ.

Класс make_pipeline

Создадим с помощью класса make_pipeline объект-контейнер, в который поместим необходимые нам инструменты.

# импортируем класс make_pipeline (упрощенный вариант класса Pipeline) из модуля pipeline

from sklearn.pipeline import make_pipeline

# создадим объект pipe, в который поместим объекты классов StandardScaler и LinearRegression

pipe = make_pipeline(StandardScaler(), LinearRegression())

pipe

1 2	Pipeline(steps=[('standardscaler', StandardScaler()), ('linearregression', LinearRegression())])

Применим метод .fit() к объекту pipe и используем обучающую выборку. Этот метод:

вызывает соответствующие методы .fit() и .transform() класса StandardScaler, т.е. рассчитывает среднее и СКО и масштабирует данные
затем вызовет метод .fit() класса LinearRegression, обучит модель на преобразованных данных и «запомнит» коэффициенты

1	pipe.fit(X_train, y_train)

1 2	Pipeline(steps=[('standardscaler', StandardScaler()), ('linearregression', LinearRegression())])

Теперь если мы применим к объекту pipe метод .predict() и передадим ему признаки тестовой части, то пайплайн вначале стандартизирует выборку с помощью рассчитанных ранее среднего и СКО обучающей выборки, а затем сделает прогноз.

1	pipe.predict(X_test)

1 2	array([0.72412832, 1.76677807, 2.71151581, ..., 1.72382152, 2.34689276, 3.52917352])

Обратите внимание, что пайплайн также позволил избежать утечки данных.

Аналогично, мы можем применить метод .score() и передать ему тестовую выборку. Этот метод выполнит масштабирование, обучит модель, сделает прогноз и посчитает метрику качества.

1	pipe.score(X_test, y_test)

1	0.5910509795491352

Замечу, что метод .score() применим только в том случае, если последний класс внутри пайплайна располагает таким методом. В нашем случае, для класса LinearRegression метод .score() задан и выдает коэффициент детерминации $R^2$.

Сделать масштабирование данных и прогноз или оценку качества модели можно в одну строчку.

1	make_pipeline(StandardScaler(), LinearRegression()).fit(X_train, y_train).predict(X_test)

1 2	array([0.72412832, 1.76677807, 2.71151581, ..., 1.72382152, 2.34689276, 3.52917352])

1	make_pipeline(StandardScaler(), LinearRegression()).fit(X_train, y_train).score(X_test, y_test)

1	0.5910509795491352

Класс make_pipeline является упрощенной версией класса Pipeline.

1	type(pipe)

1	sklearn.pipeline.Pipeline

Класс Pipeline

Для того чтобы создать объект класса Pipeline, этому классу нужно передать кортежи из названия инструмента и соответствующего класса.

# испортируем класс Pipeline

from sklearn.pipeline import Pipeline

# задаем названия и создаем объекты используемых классов

pipe = Pipeline(steps = [('scaler', StandardScaler()),

('lr', LinearRegression())],

verbose = True)

Обратите внимание на параметр verbose. Он используется во многих классах и функциях. Изначально, verbose по-английский означает «склонный к многословности, болтливый [человек]», применительно к программированию — это детальный вывод хода выполнения программы.

1 2	# рассчитаем коэффициент детерминации pipe.fit(X_train, y_train).score(X_test, y_test)

[Pipeline] ............ (step 1 of 2) Processing scaler, total= 0.0s

[Pipeline] ................ (step 2 of 2) Processing lr, total= 0.0s

0.5910509795491352

Нормализация среднего

Нормализация среднего (mean normalization) предполагает деление разности между значением и средним признака не на СКО, а на диапазон от минимального до максимального значения.

$$ x’ = \frac{x-\mu}{x_{max}-x_{min}} $$

Перейдем к другим способам масштабирования.

Приведение к диапазону

Приведение признаков к заданному диапазону (scaling features to a range) является альтернативой стандартизации в тех случаях, когда нормальное распределение не является условием для обучения алгоритма. Рассмотрим два инструмента: MinMaxScaler и MaxAbsScaler.

MinMaxScaler

MinMax Scaler приводит данные к заданному диапазону (по умолчанию к промежутку от 0 до 1). Приведем формулу.

$$ x’ = \frac{x-x_{min}}{x_{max}-x_{min}} $$

Если мы хотим привести данные к произвольному диапазону [a, b], то можем воспользоваться общей формулой.

$$ x’ = a+\frac{(x-x_{min})(b-a)}{x_{max}-x_{min}} $$

Дополнительно замечу, что при работе с изображениями, если скажем на черно-белой фотографии каждый пиксель имеет диапазон от 0 до 255, то для приведения всех пикселей к диапазону от 0 до 1 достаточно разделить каждое значение на 255.

Применим класс MinMaxScaler к нашим данным.

# импортируем класс MinMaxScaler

from sklearn.preprocessing import MinMaxScaler

# создаем объект этого класса,

# в параметре feature_range оставим диапазон по умолчанию

minmax = MinMaxScaler(feature_range = (0, 1))

minmax

1	MinMaxScaler()

# применим метод .fit() и

minmax.fit(boston)

# найдем минимальные и максимальные значения

minmax.data_min_, minmax.data_max_

1	(array([1.73, 5. ]), array([37.97, 50. ]))

# приведем данные без выбросов (достаточно метода .transform())

boston_scaled = minmax.transform(boston)

# и с выбросами к заданному диапазону

boston_outlier_scaled = minmax.fit_transform(boston_outlier)

# преобразуем результаты в датафрейм

boston_scaled = pd.DataFrame(boston_scaled, columns = boston.columns)

boston_outlier_scaled = pd.DataFrame(boston_outlier_scaled, columns = boston.columns)

Визуально оценим результат.

# построим точечные диаграммы

scatter_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'MinMaxScaler')

# и гистограммы

hist_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'MinMaxScaler')

Этот метод также чувствителен к выбросам и при их наличии не обеспечивает⧉ единого масштаба признаков.

MaxAbsScaler

Стандартизация разреженных данных

Работая с рекомендательными системами, мы увидели, что данные могут храниться в разреженных матрицах (sparse matrices). Приведем простой пример.

# создадим разреженную матрицу с пятью признаками

sparse_data = {}

sparse_data['F1'] = [0, 0, 1.25, 0, 2.15, 0, 0, 0, 0, 0, 0, 0]

sparse_data['F2'] = [0, 0, 0, 0.45, 0, 1.20, 0, 0, 0, 1.28, 0, 0]

sparse_data['F3'] = [0, 0, 0, 0, 2.15, 0, 0, 0, 0.33, 0, 0, 0]

sparse_data['F4'] = [0, -6.5, 0, 0, 0, 0, 8.25, 0, 0, 0, 0, 0]

sparse_data['F5'] = [0, 0, 0, 0, 0, 3.17, 0, 0, 0, 0, 0, -1.85]

sparse_data = pd.DataFrame(sparse_data)

sparse_data

Если применить, например, стандартизацию, то в соответствии с формулой этого преобразования нули заполнятся другими отличными от нуля значениями.

1 2	pd.DataFrame(StandardScaler().fit_transform(sparse_data), columns = sparse_data.columns).round(2)

Таким образом мы испортим наши данные. Для того чтобы этого избежать можно использовать MaxAbsScaler.

Примечание. MinMaxScaler, в чем вы можете убедиться самостоятельно, справится с сохранением нулей в столбцах, где есть только положительные значения, и не справится со столбцами с отрицательными значениями.

Формула и простой пример

Приведем формулу.

$$ x’ = \frac{x}{|x_{max}|} $$

В данном случае мы делим каждое значение на модуль максимального значения признака. Посмотрим на простом примере, что в этом случае происходит с данными.

# создадим двумерный массив

arr = np.array([[ 1., -1., -2.],

[ 2., 0., 0.],

[ 0., 1., 1.]])

# применим MaxAbsScaler

from sklearn.preprocessing import MaxAbsScaler

maxabs = MaxAbsScaler()

maxabs.fit_transform(arr)

array([[ 0.5, -1. , -1. ],

[ 1. , 0. , 0. ],

[ 0. , 1. , 0.5]])

1 2	# выведем модуль максимального значения каждого столбца maxabs.scale_

1	array([2., 1., 2.])

В качестве примера разберем первый столбец. Максимальным значением по модулю будет два и именно на это число мы делим каждое значение признака.

Отметим некоторые особенности преобразования MaxAbsScaler:

нулевые значения сохраняются
только положительные значения столбца приводятся к диапазону от 0 до 1 и здесь MaxAbsScaler работает так же, как и MinMaxScaler
только отрицательные значения приводятся к диапазону от −1 до 0
положительные и отрицательные значения — к диапазону от −1 до 1

Разреженная матрица и MaxAbsScaler

Применим MaxAbsScaler к разреженной матрице.

1 2	pd.DataFrame(MaxAbsScaler().fit_transform(sparse_data), columns = sparse_data.columns).round(2)

применение MaxAbsScaler к разреженной матрице

Матрица csr и MaxAbsScaler

Как мы знаем, разреженные матрицы удобно хранить в формате сжатого хранения строкой (сompressed sparse row, csr), и мы можем применить MaxAbsScaler непосредственно к данным в этом формате.

# создадим матрицу в формате сжатого хранения строкой

from scipy.sparse import csr_matrix

csr_data = csr_matrix(sparse_data.values)

print(csr_data)

(1, 3) -6.5

(2, 0) 1.25

(3, 1) 0.45

(4, 0) 2.15

(4, 2) 2.15

(5, 1) 1.2

(5, 4) 3.17

(6, 3) 8.25

(8, 2) 0.33

(9, 1) 1.28

(11, 4) -1.85

# применим MaxAbsScaler

csr_data_scaled = MaxAbsScaler().fit_transform(csr_data)

print(csr_data_scaled)

(1, 3) -0.7878787878787878

(2, 0) 0.5813953488372093

(3, 1) 0.3515625

(4, 0) 1.0

(4, 2) 1.0

(5, 1) 0.9375

(5, 4) 0.9999999999999999

(6, 3) 1.0

(8, 2) 0.15348837209302327

(9, 1) 1.0

(11, 4) -0.583596214511041

1 2	# восстановим плотную матрицу csr_data_scaled.todense().round(2)

array([[ 0. , 0. , 0. , 0. , 0. ],

[ 0. , 0. , 0. , -0.79, 0. ],

[ 0.58, 0. , 0. , 0. , 0. ],

[ 0. , 0.35, 0. , 0. , 0. ],

[ 1. , 0. , 1. , 0. , 0. ],

[ 0. , 0.94, 0. , 0. , 1. ],

[ 0. , 0. , 0. , 1. , 0. ],

[ 0. , 0. , 0. , 0. , 0. ],

[ 0. , 0. , 0.15, 0. , 0. ],

[ 0. , 1. , 0. , 0. , 0. ],

[ 0. , 0. , 0. , 0. , 0. ],

[ 0. , 0. , 0. , 0. , -0.58]])

MaxAbsScaler также чувствителен к выбросам⧉.

RobustScaler

В отличие от приведенных выше инструментов, RobustScaler более устойчив к выбросам⧉ в силу того, что усреднение происходит по разнице между третьим и первым квартилями, то есть робастными статистическими показателями.

$$ x = \frac{x-Q_1(x)}{Q_3(x)-Q_1(x)} $$

Применим класс RobustScaler.

from sklearn.preprocessing import RobustScaler

boston_scaled = RobustScaler().fit_transform(boston)

boston_outlier_scaled = RobustScaler().fit_transform(boston_outlier)

boston_scaled = pd.DataFrame(boston_scaled, columns = boston.columns)

boston_outlier_scaled = pd.DataFrame(boston_outlier_scaled, columns = boston.columns)

Посмотрим на преобразование на графике.

scatter_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'RobustScaler')

hist_plots(boston,

boston_outlier,

boston_scaled,

boston_outlier_scaled,

title = 'RobustScaler')

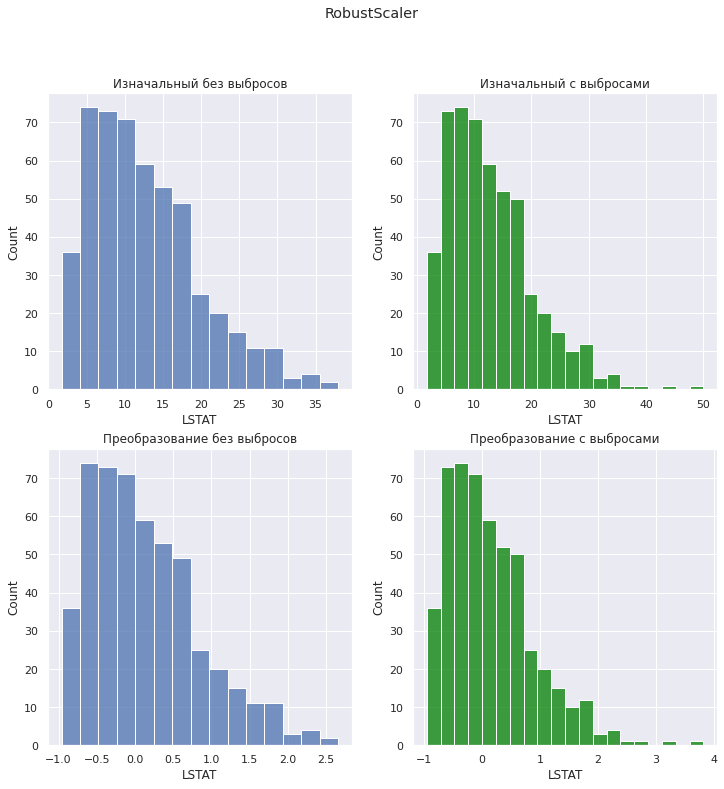
RobustScaler не приводит данные строго к одному диапазону и не меняет структуру распределения (и в частности не изменяет расстояние между основной массой данных и выбросами).

Класс Normalizer

Класс Normalizer, в отличие от предыдущих инструментов, по умолчанию приводит наблюдения (то есть строки, а не столбцы датафрейма) к единичной норме (или длине вектора, равной единице, unit norm, unit vector) или нормализует (normalizes) их.

В рамках вводного курса мы уже говорили, что каждое наблюдение можно представить в качестве вектора в n-мерном пространстве.

Понятие нормы вектора

Прежде чем говорить про нормализацию разберём понятие нормы вектора. Под нормой понимается такая функция, которая ставит в соответствие вектору в n-мерном пространстве некоторое число.

Это число часто рассматривают как длину вектора от начала координат до конца вектора. Причем эту длину или расстояние можно измерять по-разному.

Рассмотрим вероятно наиболее распространенное Евклидово расстояние (Eucledean distance) или как ещё говорят L2 норму (L2 norm) вектора $\textbf{x}$ с координатами ${x_1, x_2,…, x_n} $ (термины длины, расстояния и нормы часто оказываются взаимозаменяемы).

$$ || \textbf{x} ||_2 = \sqrt{x_1^2 + x_2^2 + … + x_n^2} $$

Другими словами, мы смотрим на какое расстояние нам необходимо сместиться в каждом из измерений, возводим это расстояние в квадрат, суммируем и извлекаем квадратный корень. Рассмотрим простой пример.

# возькм вектор с координатами [4, 3]

v = np.array([4, 3])

# и найдем его длину или L2 норму

l2norm = np.sqrt(v[0]**2 + v[1]**2)

l2norm

5.0

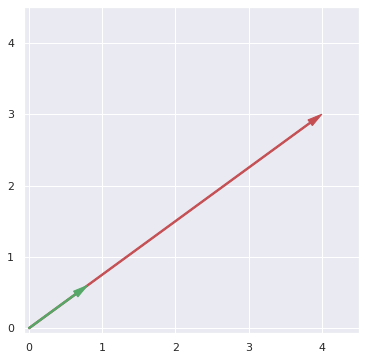
Если каждый компонент вектора разделить на L2 норму, то его длина или расстояние по прямой от начала координат до конца вектора было бы равно единице.

# разделим каждый компонент вектора на его норму

v_normalized = v/l2norm

v_normalized

1	array([0.8, 0.6])

Это и есть L2 нормализация.

# выведем оба вектора на графике

plt.figure(figsize = (6, 6))

ax = plt.axes()

plt.xlim([-0.07, 4.5])

plt.ylim([-0.07, 4.5])

ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = 'r', ec = 'r')

ax.arrow(0, 0, v_normalized[0], v_normalized[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = 'g', ec = 'g')

plt.show()

L2 нормализация

Возьмём простой двумерный массив данных, вручную выполним построчную L2 нормализацию, а затем с помощью класса Normalizer проверим результат.

# каждая строка - это вектор

arr = np.array([[45, 30],

[12, -340],

[-125, 4]])

1 2	# найдем L2 норму первого вектора np.sqrt(arr[0][0] 2 + arr[0][1] 2)

1	54.08326913195984

# в цикле пройдемся по строкам

for row in arr:

# найдем L2 норму каждого вектора-строки

l2norm = np.sqrt(row[0] ** 2 + row[1] ** 2)

# и разделим на нее каждый из компонентов вектора

print((row[0]/l2norm).round(8), (row[1]/l2norm).round(8))

0.83205029 0.5547002

0.03527216 -0.99937774

-0.99948839 0.03198363

# убедимся, что L2 нормализация выполнена верно,

# подставив в формулу Евклидова расстояния новые координаты

np.sqrt(0.83205029 ** 2 + 0.5547002 ** 2).round(3)

1.0

# выполним ту же операцию с помощью класса Normalizer

from sklearn.preprocessing import Normalizer

Normalizer().fit_transform(arr)

array([[ 0.83205029, 0.5547002 ],

[ 0.03527216, -0.99937774],

[-0.99948839, 0.03198363]])

Графически конец каждого L2 нормализованного вектора оказывается на единичной окружности (то есть окружность с радиусом, равным единице).

plt.figure(figsize = (6, 6))

ax = plt.axes()

# в цикле нормализуем каждый из векторов

for v in Normalizer().fit_transform(arr):

# и выведем его на графике в виде стрелки

ax.arrow(0, 0, v[0], v[1], width = 0.01, head_width = 0.05, head_length = 0.05, length_includes_head = True, fc = 'g', ec = 'g')

# добавим единичную окружность

circ = plt.Circle((0, 0), radius = 1, edgecolor = 'b', facecolor = 'None', linestyle = '--')

ax.add_patch(circ)

plt.xlim([-1.2, 1.2])

plt.ylim([-1.2, 1.2])

plt.title('L2 нормализация')

plt.show()

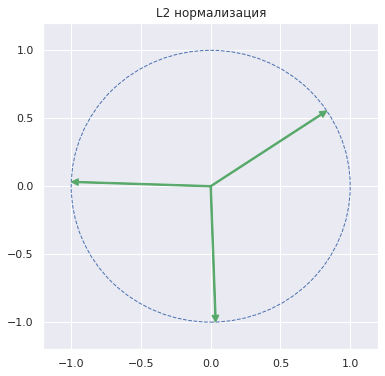
Этот метод подходит для алгоритмов, основанных на расстоянии между векторами. В частности, вспомним формулу косинусного сходства.

$$ \cos{ \theta } = \frac{\textbf{a} \cdot \textbf{b}}{|| \textbf{a} ||_2 || \textbf{b} ||_2} $$

В знаменателе уже заложена L2 нормализация. По сути, мы вначале приводим каждый вектор к L2 норме, равной одному, а затем с помощью скалярного произведения находим косинус угла между ними.

Опасность нормализации по строкам

С точки зрения масштабирования данных у такого подхода есть один недостаток. Нормализация по строкам разрушает связи внутри признаков. Рассмотрим массив, в котором строки это люди, а столбцы — данных о них (в частности, рост, вес и возраст).

# данные о росте, весе и возрасте людей

people = np.array([[180, 80, 50],

[170, 73, 50]])

Как мы видим, обоим людям по 50 лет. Проведем L2 нормализацию по строкам.

1 2	# получается, что у них разный возраст Normalizer().fit_transform(people)

Как мы видим, после нормализации получается, что возраст у них разный.

1 2	array([[0.8857221 , 0.39365427, 0.24603392], [0.88704238, 0.38090643, 0.26089482]])

По этой причине проводить масштабирование по строкам можно только в том случае, если связи между наблюдениями внутри признаков не имеют значения (другими словами, вам не важно, что в новых данных люди с одинаковым возрастом получают разные значения).

L1 нормализация

Как уже было сказано длину вектора не обязательно измерять по формуле Евклидова расстояния. Можно воспользоваться формулой расстояния городских кварталов (Manhattan distance, taxicab distance) или L1 нормой (L1 norm).

$$ || \textbf{x} ||_1 = |x_1| + |x_2| + … + |x_n| $$

По большому счету, вместо возведения в квадрат мы находим модуль каждой координаты вектора. При этом извлекать квадратный корень для возвращения к исходным единицам измерения уже нет необходимости.

1 2	# возьмем то же массив arr

array([[ 45, 30],

[ 12, -340],

[-125, 4]])

1 2	# рассчитаем L1 норму для первой строки np.abs(arr[0][0]) + np.abs(arr[0][1])

# вновь пройдемся по каждому вектору

for row in arr:

# найдем соответствующую L1 норму

l1norm = np.abs(row[0]) + np.abs(row[1])

# и нормализуем векторы

print((row[0]/l1norm).round(8), (row[1]/l1norm).round(8))

0.6 0.4

0.03409091 -0.96590909

-0.96899225 0.03100775

Теперь к единичной норме приведена сумма модулей координат вектора.

1 2	# убедимся в том, что вторая вектор-строка имеет единичную L1 норму np.abs(0.03409091) + np.abs(-0.96590909)

1.0

Сравним результат с объектом класса Normalizer.

# через параметр norm = 'l1' укажем,

# что хотим провести L1 нормализацию

Normalizer(norm = 'l1').fit_transform(arr)

array([[ 0.6 , 0.4 ],

[ 0.03409091, -0.96590909],

[-0.96899225, 0.03100775]])

Теперь выведем L1 нормализованные векторы на графике и посмотрим, как рассчитывалось расстояние до первого вектора.

plt.figure(figsize = (6, 6))

ax = plt.axes()

# выведем L1 нормализованные векторы

for v in Normalizer(norm = 'l1').fit_transform(arr):

ax.arrow(0, 0, v[0], v[1], width = 0.01, head_width = 0.05, head_length = 0.05, length_includes_head = True, fc = 'g', ec = 'g')

# то, как рассчитывалось расстояние до первого вектора

ax.arrow(0, 0, 0.6, 0, width = 0.005, head_width = 0.03, head_length = 0.05, length_includes_head = True, fc = 'k', ec = 'k', linestyle = '--')

ax.arrow(0.6, 0, 0, 0.4, width = 0.005, head_width = 0.03, head_length = 0.05, length_includes_head = True, fc = 'r', ec = 'r', linestyle = '--')

# а также границы единичных векторов при L1 нормализации

points = [[1, 0], [0, 1], [-1, 0], [0, -1]]

polygon= plt.Polygon(points, fill = None , edgecolor = 'b', linestyle = '--')

ax.add_patch(polygon)

plt.xlim([-1.2, 1.2])

plt.ylim([-1.2, 1.2])

plt.title('L1 нормализация')

plt.show()

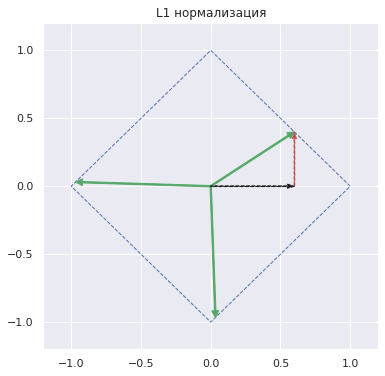
Из графика выше становится очевидно, почему это расстояние L1 (то есть сумма черного и красного векторов, для L1 нормализованного вектора равная единице) называется Manhattan distance или taxicab distance. Водителю такси на Манхэттене, основанном на гипподамовой системе с прямоугольными кварталами, чтобы попасть из точки А в точку Б пришлось бы двигаться строго перпендикулярными отрезками.

Расстояние Минковского

Обобщением Евклидова расстояния и расстояния городских кварталов будет расстояние Минковского (Minkowski distance).

$$ || \textbf{x} ||_p = \left( \sum_{i=1}^n { |x_i|^p } \right) ^{\frac{1}{p}} $$

где $p=1$ и $p=2$ — это соответственно метрика городских кварталов и Евклидово расстояние.

Расстояние Чебышёва

Что интересно, если p стремится к бесконечности, то формула расстояния принимает вид.

$$ \lim_{p\to\infty} \left( \sum_{i=1}^n { |x_i|^p } \right) ^{\frac{1}{p}} = \max_{i=1}^n | x_i | $$

Такое расстояние называется расстоянием Чебышёва (Chebyshev distance). По сути для расчета этого расстояния мы берем наибольшую по модулю координату вектора.

1 2	# найдем расстояние Чебышёва для первого вектора max(np.abs(arr[0][0]), np.abs(arr[0][1]))

# теперь для всего массива

for row in arr:

# найдем соответствующую норму Чебышёва

l_inf = max(np.abs(row[0]), np.abs(row[1]))

# и нормализуем векторы

print((row[0]/l_inf).round(8), (row[1]/l_inf).round(8))

1.0 0.66666667

0.03529412 -1.0

-1.0 0.032

Для нормализации векторов по расстоянию Чебышёва классу Normalizer нужно передать параметр norm = ‘max’.

1	Normalizer(norm = 'max').fit_transform(arr)

array([[ 1. , 0.66666667],

[ 0.03529412, -1. ],

[-1. , 0.032 ]])

Графически в двумерном пространстве нормализованные таким образом векторы располагаются на квадрате, стороны которого имеют длину, равную двум, и параллельны осям координат.

plt.figure(figsize = (6, 6))

ax = plt.axes()

# выведем нормализованные по расстоянию Чебышёва векторы

for v in Normalizer(norm = 'max').fit_transform(arr):

ax.arrow(0, 0, v[0], v[1], width = 0.01, head_width = 0.05, head_length = 0.05, length_includes_head = True, fc = 'g', ec = 'g')

# а также границы единичных векторов при такой нормализации

points = [[1, 1], [1, -1], [-1, -1], [-1, 1]]

polygon= plt.Polygon(points, fill = None , edgecolor = 'b', linestyle = '--')

ax.add_patch(polygon)

plt.xlim([-1.2, 1.2])

plt.ylim([-1.2, 1.2])

plt.title('Нормализация Чебышёва')

plt.show()

Про терминологию

Терминология способов преобразования количественных данных пока окончально не устоялась. Например, часто под нормализацией понимают приведение данных к диапазону от 0 до 1 или в целом весь процесс масштабирования данных.

На практике бывает полезно сообщать, какую именно линейную трансформацию вы применяете к данным (а не только ее название), либо приводить название используемого инструмента.

Перейдем к нелинейным преобразованиям.