Все курсы > Вводный курс > Занятие 20
Понятие временного ряда
Временной ряд (time series) — это данные, последовательно собранные в регулярные промежутки времени.
К таким данным относятся, например, цены на акции, объемы продаж чего-либо, изменения температуры с течением времени и т.д. Посмотрим на изменение обычных данных и временных рядов.

Основное отличие: перекрестные данные предполагают независимость наблюдений, во временных рядах будущее зависит от прошлого.
Работа с временными рядами предполагает два аспекта:
- Анализ временного ряда (time series analysis), т.е. понимание его структуры и закономерностей; и
- Моделирование и построение прогноза на будущее (time series forecasting)
Договоримся о терминах:
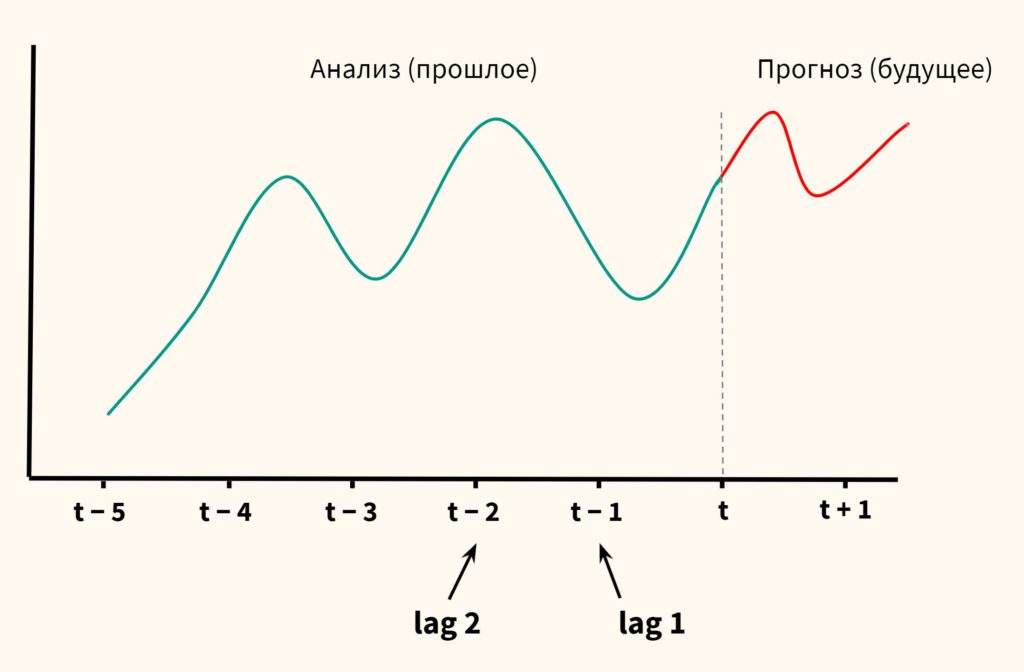
- Во-первых, определим нотацию периодов. Временем t обозначим настоящее, t−1, t−2,… прошлое, t+1, t+2,… будущее.
- Во-вторых, введем важное понятие временного лага (lag), т.е. запаздывания по сравнению с заданным периодом.
Датасеты
Мы будем использовать два популярных набора данных, а именно (1) ежемесячные данные о количестве пассажиров, перевезенных одной американской авиакомпанией с 1949 по 1960 годы и (2) ежедневные данные о родившихся в Калифорнии в 1959 году девочках.
Подгружать внешние данные в ноутбук Google Colab мы уже умеем. Можем переходить непосредственно к работе с кодом.
Откроем ноутбук к этому занятию⧉
Анализ временных рядов
|
1 2 3 4 |
# импортируем необходимые библиотеки import pandas as pd import numpy as np import matplotlib.pyplot as plt |
Импорт данных и работа в библиотеке Pandas
Для начала давайте импортируем данные. Пока что мы будем использовать только первый набор данных с информацией об авиаперевозках.
|
1 2 3 |
# импортируем файл с данными о пассажирах passengers = pd.read_csv("/content/passengers.csv") passengers.head() |

Сделаем дату индексом.
|
1 2 3 |
# превратим дату в индекс и сделаем изменение постоянным passengers.set_index('Month', inplace = True) passengers.head() |

Питон воспринимает дату как число. Это не очень удобно, если мы хотим делать срезы и в целом изменять данные во времени. Дату можно преобразовать в специальный объект datetime.
|
1 2 3 4 5 |
# превратим дату (наш индекс) в объект datetime passengers.index = pd.to_datetime(passengers.index) # посмотрим на первые пять дат и на тип данных passengers.index[:5] |
|
1 2 3 |
DatetimeIndex(['1949-01-01', '1949-02-01', '1949-03-01', '1949-04-01', '1949-05-01'], dtype='datetime64[ns]', name='Month', freq=None) |
Все эти операции также можно проделать в одну строчку.
|
1 |
passengers = pd.read_csv('/content/passengers.csv', index_col = 'Month', parse_dates = True) |
Теперь мы можем делать срезы за определенный период, например, с августа 1949 по март 1950 года.
|
1 |
passengers['1949-08':'1950-03'] |
Обратите внимание, что в отличие от других перечней в Питоне (например, списков), во временном ряде мы получаем данные и по начальной, и по конечной дате среза (в частности, март 1950 года вошел в наш интервал).
Изменение шага временного ряда, сдвиг и скользящее среднее
Отдельно хотелось бы поговорить про возможность обобщения и изменения данных. Помимо прочего, мы можем изменить шаг (resample) нашего временного ряда, и посмотреть средние показатели перевозок, например, за год.
|
1 |
passengers.resample(rule = 'AS').mean().head() |

Кроме того, мы можем сдвинуть (shift) наши данные на n периодов вперед или назад.
|
1 2 |
# произведем сдвиг на два периода (в данном случае месяца) вперед passengers.shift(2, axis = 0).head() |

Что логично, после сдвига первые два значения определяются как пропущенные (NaN или Not a number).
Мы также можем рассчитать скользящее среднее (moving average, rolling average) за n предыдущих периодов. Вначале посмотрим, что это такое.

Теперь давайте рассчитаем его для наших данных. Период, за который рассчитывается скользящее среднее, также называется окном (window).
|
1 2 |
# рассчитаем скользящее среднее для трех месяцев passengers.rolling(window = 3).mean().head() |

Опять же, так как в данном случае мы использовали три месяца для расчета скользящего среднего, этот показатель недоступен для первых двух значений. В целом, скользящее среднее сглаживает временные показатели (мы это увидим на графике в следующем разделе).
Построение графиков
Для того чтобы построить график временного ряда мы можем воспользоваться инструментами, которые уже содержатся в библиотеке Pandas. Например, простым методом .plot().
|
1 |
passengers.plot() |

График можно усложнить.
|
1 2 3 |
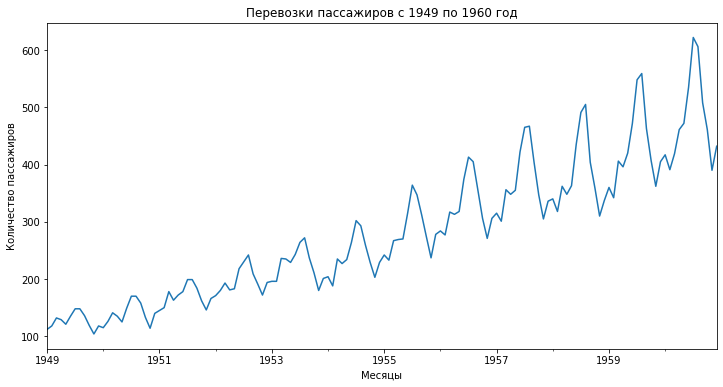
# изменим размер графика, уберем легенду и добавим подписи ax = passengers.plot(figsize = (12,6), legend = None) ax.set(title = 'Перевозки пассажиров с 1949 по 1960 год', xlabel = 'Месяцы', ylabel = 'Количество пассажиров') |
Визуализацию можно также построить с помощью библиотеки Matplotlib. Давайте выведем на одном графике перевозки пассажиров и скользящее среднее.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# зададим размер графика plt.figure(figsize = (15,8)) # поочередно зададим кривые (перевозки и скользящее среднее) с подписями и цветом plt.plot(passengers, label = 'Перевозки пассажиров по месяцам', color = 'steelblue') plt.plot(passengers.rolling(window = 12).mean(), label = 'Скользящее среднее за 12 месяцев', color = 'orange') # добавим легенду, ее положение на графике и размер шрифта plt.legend(title = '', loc = 'upper left', fontsize = 14) # добавим подписи к осям и заголовки plt.xlabel('Месяцы', fontsize = 14) plt.ylabel('Количество пассажиров', fontsize = 14) plt.title('Перевозки пассажиров с 1949 по 1960 год', fontsize = 16) # выведем обе кривые на одном графике plt.show() |

Как вы видите, скользящее среднее сильно сглаживает показатели. Также обратите внимание, что так как в данном случае мы взяли окно равное двенадцати месяцам, то первое значение скользящего среднего мы получили только за декабрь 1949 года (самое начало желтой кривой на графике).
В целом не стоит недооценивать важность визуальной оценки ряда на графике. Многие особенности можно выявить именно так.
Разложение временного ряда на компоненты
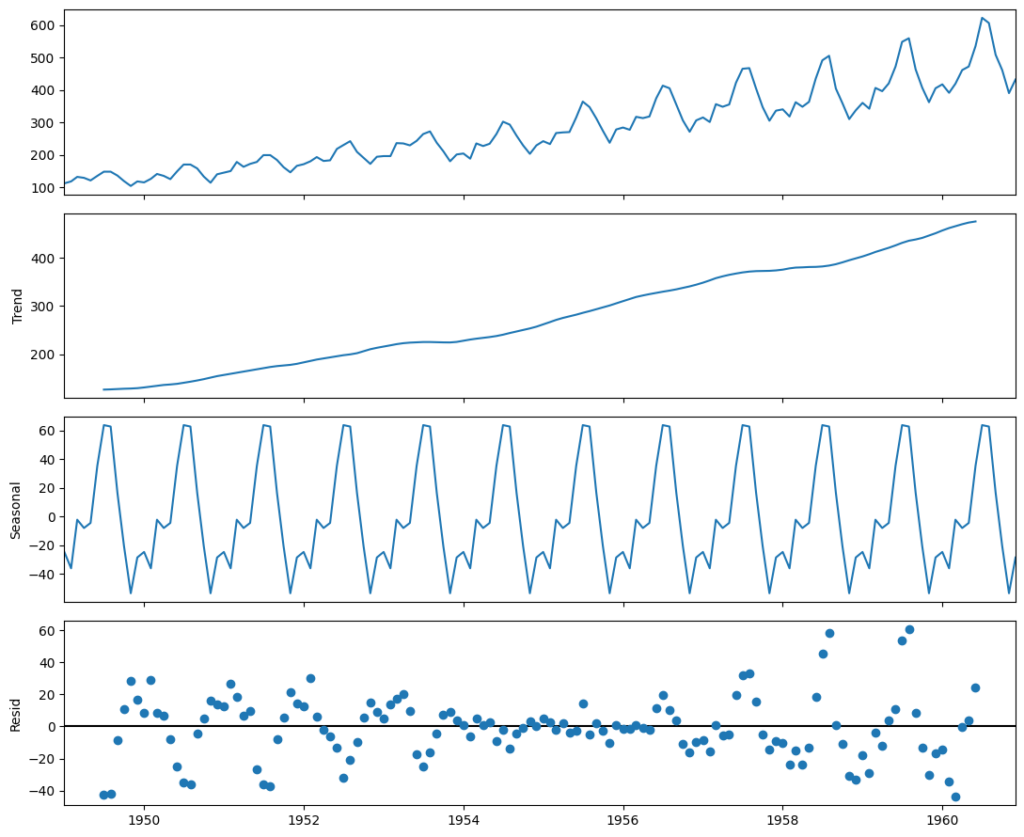
Выявление компонентов временного ряда (time series decomposition) предполагает его разложение на тренд, сезонность и случайные колебания. Дадим несколько неформальных определений.
- Тренд — долгосрочное изменение уровня ряда
- Сезонность предполагает циклические изменения уровня ряда с постоянным периодом
- Случайные колебания — непрогнозируемое случайное изменение ряда
В Питоне в модуле statsmodels есть функция seasonal_decompose(). Воспользуемся ей для визуализации компонентов ряда.
Перед этим импортируем второй датасет для последующего сравнения.
|
1 2 3 4 |
# для наглядности импортируем второй датасет # сразу превратим дату в индекс и преобразуем ее в объект datetime births = pd.read_csv('/content/births.csv', index_col = 'Date', parse_dates = True) births.head(3) |

Теперь давайте разложим наш временной ряд по авиаперевозкам на компоненты.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# импортируем функцию seasonal_decompose из statsmodels from statsmodels.tsa.seasonal import seasonal_decompose # задаем размер графика from pylab import rcParams rcParams['figure.figsize'] = 11, 9 # применяем функцию к данным о перевозках decompose = seasonal_decompose(passengers) decompose.plot() plt.show() |
Сделаем то же самое с данными о рождаемости.
|
1 2 3 4 |
decompose = seasonal_decompose(births) decompose.plot() plt.show() |

Как мы видим, графики совершенно разные. В следующем разделе мы изучим это различие более подробно.
Стационарность
Стационарность (stationarity) временного ряда как раз означает, что такие компоненты как тренд и сезонность отсутствуют. Говоря более точно, среднее значение и дисперсия не меняются со смещением во времени.
Понимание того, стационарные ли у нас данные или нестационарные важно для последующего моделирования.
Стационарность процесса можно оценить визуально. Датасет о перевозках демонстрирует очевидный тренд и сезонность, в то время как в наборе данных о рождаемости этого не видно (см. графики выше).
Для более точной оценки стационарности можно применить тест Дики-Фуллера (Dickey-Fuller test). О том, что такое статистический вывод мы с вами уже говорили.
В данном случае гипотезы звучат следующим образом.
- Нулевая гипотеза предполагает, что процесс нестационарный
- Альтернативная гипотеза соответственно говорит об обратном
Применим этот тест к обоим датасетам. Используем пороговое значение, равное 0,05 (5%).
|
1 2 3 4 5 6 7 8 |
# импортируем необходимую функцию from statsmodels.tsa.stattools import adfuller # передадим ей столбец с данными о перевозках и поместим результат в adf_test adf_test = adfuller(passengers['#Passengers']) # выведем p-value print('p-value = ' + str(adf_test[1])) |
|
1 |
p-value = 0.991880243437641 |
Как мы видим, вероятность (p-value) для данных о перевозках существенно выше 0,05. Мы не можем отвергнуть нулевую гипотезу. Процесс нестанионарный. Проведем тест для второго набора данных.
|
1 2 3 4 5 |
# теперь посмотрим на данные о рождаемости adf_test = adfuller(births['Births']) # выведем p-value print('p-value = ' +str(adf_test[1])) |
|
1 |
p-value = 5.2434129901498554e-05 |
Результат существенно меньше 5%. Временной ряд стационарен.
Надо сказать, что наша визуальная оценка полностью совпала с математическими вычислениями.
Автокорреляция
Изучая статистику, мы с вами уже познакомились с корреляцией. Корреляция показывает силу взаимосвязи двух переменных и позволяет строить модель.
Автокорреляция также показывает степень взаимосвязи в диапазоне от –1 до 1, но только не двух переменных, а одной и той же переменной в разные моменты времени.
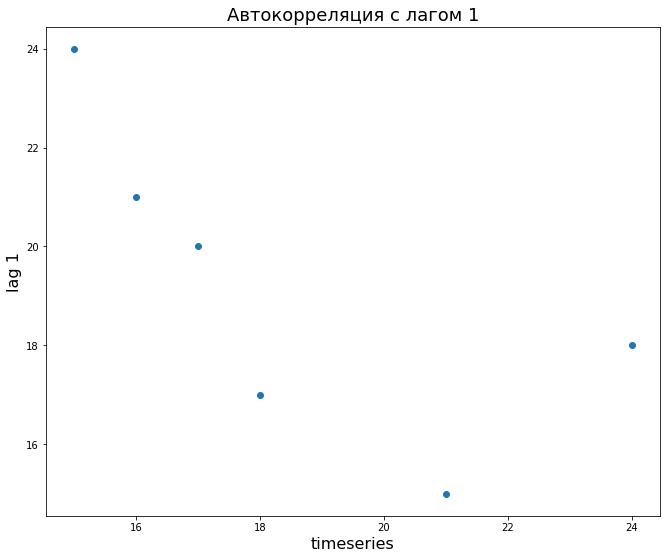
Допустим, у нас есть временной ряд и этот же ряд, взятый с лагом 1, 2 и 3.

Мы можем посчитать автокорреляцию ряда с лагом 1.
|
1 2 3 4 5 6 7 8 9 |
# для начала возьмем искусственные данные data = np.array([16, 21, 15, 24, 18, 17, 20]) # для сдвига на одно значение достаточно взять этот ряд, начиная со второго элемента lag_1 = data[1:] # посчитаем корреляцию для лага 1 (у исходных данных мы убрали последний элемент) # так как мы получим корреляционную матрицу, возьмем первую строку и второй столбец [0, 1] np.round(np.corrcoef(data[:-1], lag_1)[0,1], 2) |
|
1 |
-0.71 |
Визуально это будет выглядеть следующим образом (вспомните график обычной корреляции).
|
1 2 3 4 5 6 7 8 9 |
# построим точечную диаграмму plt.scatter(data[:-1], lag_1) # добавим подписи plt.xlabel('timeseries', fontsize = 16) plt.ylabel('lag 1', fontsize = 16) plt.title('Автокорреляция с лагом 1', fontsize = 18) plt.show() |
Аналогично мы можем посчитать корреляцию для лагов 2 и 3 и на самом деле любого другого лага. Такие измерения автокорреляции удобно вычислить и изобразить с помощью графика автокорреляционной функции (autocorrelation function, ACF).
|
1 2 3 4 5 6 7 8 9 |
# импортируем автокорреляционную функцию (ACF) from statsmodels.graphics.tsaplots import plot_acf # применим функцию к нашему набору данных plot_acf(data, lags = np.arange(len(data)), alpha = None) # добавим отступы сверху и снизу на графике plt.axis('tight') plt.show() |

В частности, мы видим, что автокорреляция ряда с самим собой (первый столбец) равна 1, что логично. Второй столбец (то есть лаг 1) как раз примерно равен – 0,71.
Разные значения, полученные через np.corrcoef() и plot_acf(), объясняются небольшим различием в заложенных в этих функциях формулах.
Теперь построим график ACF для наших данных о перевозках.
|
1 2 3 4 |
# применим ее к данным о пассажирах plot_acf(passengers) plt.axis('tight') plt.show() |

Автокорреляция позволяет выявлять тренд и сезонность, а также используется при подборе параметров моделей. В частности, мы видим, что лаг 12 сильнее коррелирует с исходным рядом, чем соседние лаги 10 и 11. То же самое можно сказать и про лаг 24. Такая автокорреляция позволяет предположить наличие (ежегодных) сезонных колебаний.
То, что корреляция постоянно положительная говорит о наличии тренда. Все это согласуется с тем, что мы узнали о данных, когда раскладывали их на компоненты.
Также замечу, что синяя граница позволяет оценить статистическую значимость корреляции. Если столбец выходит за ее пределы, то автокорреляция достаточно сильна и ее можно использовать при построении модели.
Сравним полученный выше график с графиком автокорреляционной функции данных о рождаемости.
|
1 2 3 4 |
# построим аналогичный график для данных о рождаемости plot_acf(births) plt.axis('tight') plt.show() |

Во-первых, важно отметить, что автокорреляция в данном случае намного слабее. Во-вторых, мы не можем выявить четкой сезонности и тренда.
Моделирование и построение прогноза
На сегодняшнем занятии мы познакомимся с двумя типами моделей: экспоненциальное сглаживание и модель ARMA (и ее более продвинутые версии, ARIMA, SARIMA и SARIMAX).
Экспоненциальное сглаживание
Вновь обратимся к скользящему среднему (см. выше). В этой модели (1) всем предыдущим наблюдениям задавался одинаковый вес и (2) количество таких наблюдений было ограничено (мы называли это размером окна).
Однако логично предположить, что недавние наблюдения более важны для прогноза, чем более отдаленные. Кроме того, мы можем взять все, а не некоторые из имеющихся у нас наблюдений.
В модели экспоненциального сглаживания (exponential smoothing) или экспоненциального скользящего среднего мы как раз (1) берем все предыдущие значения и (2) задаем каждому из наблюдений определенный вес и (экспоненциально) уменьшаем этот вес по мере углубления в прошлое.
Приведем формулу.
$$ \hat{y}_{t+1} = \alpha \cdot y_t + (1-\alpha) \cdot \hat{y}_{t} $$
где $ \hat{y}_{t+1} $ — это будущее прогнозное значение, $ y_t $ — истинное значение в текущий период, $\hat{y}_{t}$ — прогнозное значение в текущий период.
Как мы видим, будущее прогнозное значение зависит как от текущего истинного, так и от текущего прогнозного значений. Важность этих значений определяется параметром $\alpha$, который варьируется от 0 до 1. Чем $\alpha$ больше, тем больший вес у истинного наблюдения.
Формула рекурсивна, т.е. каждый раз мы умножаем ($1-\alpha$) на очередное прогнозное значение и так до конца временного ряда.
Практика
На Питоне эту модель не сложно прописать руками.
|
1 2 3 4 5 6 7 8 9 10 11 |
alpha = 0.2 # первое значение совпадает со значением временного ряда exp_smoothing = [births['Births'][0]] # в цикле for последовательно применяем формулу ко всем элементам ряда for i in range(1, len(births['Births'])): exp_smoothing.append(alpha * births['Births'][i] + (1 - alpha) * exp_smoothing[i - 1]) # выведем прогнозное значение для 366-го дня (1 января 1960 года) exp_smoothing[-1] |
|
1 |
46.6051933602952 |
Для временного ряда, состоящего из 365 наблюдений (весь 1959 год), мы получим 365 прогнозных значений (вплоть до 1 января 1960 года включительно).
|
1 |
len(births), len(exp_smoothing) |
|
1 |
(365, 365) |
Теперь добавим эти данные в исходный датафрейм births.
|
1 2 3 |
# добавим кривую сглаживаия в качестве столбца в датафрейм births['Exp_smoothing'] = exp_smoothing births.tail(3) |

Единственный нюанс, так как фактические значения описывают период с 1 января по 31 декабря 1959 года, а прогнозные со 2 января 1959 года по 1 января 1960, мы не можем просто их соединить. Второй столбец нужно сдвинуть на один день вперед.
|
1 2 3 4 5 6 7 8 9 |
# для этого импортируем класс timedelta from datetime import timedelta # возьмём последний индекс (31 декабря 1959 года) last_date = births.iloc[[-1]].index # # "прибавим" один день last_date = last_date + timedelta(days = 1) last_date |
|
1 |
DatetimeIndex(['1960-01-01'], dtype='datetime64[ns]', name='Date', freq=None) |
|
1 2 3 4 5 |
# добавим его в датафрейм births = pd.concat([births, pd.DataFrame(index = last_date)]) # значения за этот день останутся пустыми births.tail() |
Сдвинем второй столбец.
|
1 |
births['Exp_smoothing'] = births['Exp_smoothing'].shift(1) |
И посмотрим на начало и конец датафрейма.
|
1 2 |
# как и должно быть первое прогнозное значение совпадает с предыдущим фактическим births.head() |

|
1 2 |
# и у нас есть прогноз на один день вперед births.tail() |

Проверим правильность расчетов, найдя последнее прогнозное значение по формуле выше.
$$ \hat{y}_{366} = 0{,}2 \times y_{355} + 0{,}8 \times \hat{y}_{355} = 0{,}2 \times 50 + 0{,}8 \times 45{,}756492 = 46{,}6051936 $$
Результаты совпадают. Теперь выведем фактические и прогнозные значения на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# зададим размер plt.figure(figsize = (15,8)) # выведем данные о рождаемости и кривую экспоненциального сглаживания plt.plot(births['Births'], label = 'Данные о рождаемости', color = 'steelblue') plt.plot(births['Exp_smoothing'], label = 'Экспоненциальное сглаживание', color = 'orange') # добавим легенду, ее положение на графике и размер шрифта plt.legend(title = '', loc = 'upper left', fontsize = 14) # добавим подписи к осям и заголовки plt.ylabel('Количество родившихся', fontsize = 14) plt.xlabel('Месяцы', fontsize = 14) plt.title('Рождаемость в 1959 году. Прогноз на 1 января 1960 года', fontsize = 16) plt.show() |

Очень советую в качестве упражнения попробовать построить график с несколькими значениями $\alpha$ от 0 до 1.
Модель экспоненциального сглаживания можно усложнить и тогда она будет улавливать тренд и сезонность. Кроме того, усложненные модели способны предсказывать более одного значения (обратите внимание, здесь мы смогли сделать прогноз лишь на один день вперёд).
Работа над ошибками. На видео в формуле экспоненциального сглаживания есть ошибка.
|
1 2 3 4 5 6 7 8 |
alpha = 0.2 # первое значение совпадает со значением временного ряда exp_smoothing = [births['Births'][0]] # в цикле for последовательно применяем формулу ко всем элементам ряда for i in range(0, len(births['Births'])): exp_smoothing.append(alpha * births['Births'][i] + (1 - alpha) * exp_smoothing[i - 1]) |
Должно быть.
|
1 2 3 4 5 6 7 8 |
alpha = 0.2 # первое значение совпадает со значением временного ряда exp_smoothing = [births['Births'][0]] # в цикле for последовательно применяем формулу ко всем элементам ряда for i in range(1, len(births['Births'])): exp_smoothing.append(alpha * births['Births'][i] + (1 - alpha) * exp_smoothing[i - 1]) |
Как вы видите расчет прогнозного значения в цикле следовало начинать с наблюдения [births['Births'][1], а не [births['Births'][0]. Из-за этого последующие результаты оказались некорректными. В лекции и ноутбуке код исправлен.
Теперь поговорим про модели семейства ARMA.
Модель ARMA
Модель ARMA состоит из двух компонентов.

Авторегрессия (autoregressive model, AR) — это регрессия ряда на собственные значения в прошлом. Другими словами, наши признаки в модели обычной регрессии мы заменяем значениями той же переменной, но за предыдущие периоды.
Когда мы прогнозируем значение в период t с помощью данных за предыдущий период (AR(1)), уравнение будет выглядеть следующим образом.
$$ y_t = c + \varphi \cdot y_{t-1} $$
где $c$ — это константа, $\varphi$ — вес модели, $ y_{t-1} $ — значение в период $t-1$.
Количество используемых предыдущих периодов определяется параметром p. Обычно записывается как AR(p).
Модель скользящего среднего (moving average, MA) помогает учесть случайные колебания или отклонения (ошибки) истинного значения от прогнозного. Можно также сказать, что модель скользящего среднего — это авторегрессия на ошибку.
Обратите внимание, что скользящее среднее временного ряда, которое мы рассмотрели выше, и модель скользящего среднего — это разные понятия.
Если использовать ошибку только предыдущего наблюдения, то уравнение будет выглядеть следующим образом.
$$ y_t = \mu + \varphi \cdot \varepsilon_{t-1} $$
где $ \mu $ — это среднее значение временного ряда, $ \varphi $ — вес модели, $ \varepsilon_{t-1} $ — ошибка в период $t-1$.
Такую модель принято называть моделью скользящего среднего с параметром q = 1 или MA(1). Разумеется, параметр q может принимать и другие значения (MA(q)).
Модель ARMA с параметрами (или как еще говорят порядками, orders) p и q или ARMA(p, q) позволяет описать любой стационарный временной ряд.
ARMA предполагает, что в данных отсутствует тренд и сезонность (данные стационарны). Если данные нестационарны, нужно использовать более сложные версии этих моделей:
- ARIMA, здесь добавляется компонент Integrated (I), который отвечает за удаление тренда (сам процесс называется дифференцированием); и
- SARIMA, эта модель учитывает сезонность (Seasonality, S)
- SARIMAX включает еще и внешние или экзогенные факторы (eXogenous factors, отсюда и буква X в названии), которые напрямую не учитываются моделью, но влияют на нее.
Параметров у модели SARIMAX больше. Их полная версия выглядит как SARIMAX(p, d, q) x (P, D, Q, s). В данном случае, помимо известных параметров p и q, у нас появляется параметр d, отвечающий за тренд, а также набор параметров (P, D, Q, s), отвечающих за сезонность.
Теперь давайте воспользуемся моделью SARIMAX для прогнозирования авиаперевозок.
Практика
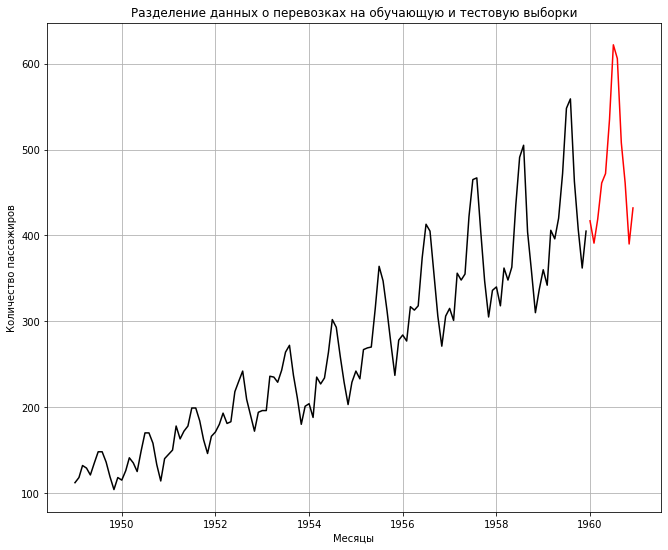
В первую очередь нужно разбить данные на обучающую и тестовую выборки. Как мы помним, у нас есть данные с января 1949 года по декабрь 1960 года.
|
1 2 3 4 5 |
# обучающая выборка будет включать данные до декабря 1959 года включительно train = passengers[:'1959-12'] # тестовая выборка начнется с января 1960 года (по сути, один год) test = passengers['1960-01':] |
Посмотрим на разделение на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
plt.plot(train, color = "black") plt.plot(test, color = "red") # заголовок и подписи к осям plt.title('Разделение данных о перевозках на обучающую и тестовую выборки') plt.ylabel('Количество пассажиров') plt.xlabel('Месяцы') # добавим сетку plt.grid() plt.show() |
Далее нам нужно обучить модель. При обучении модели SARIMAX, самое важное — правильно подобрать гиперпараметры, о которых говорилось выше. Процесс подбора гиперпараметров достаточно сложен, и сегодня мы воспользуемся уже готовыми значениями.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# принудительно отключим предупреждения системы import warnings warnings.simplefilter(action = 'ignore', category = Warning) # обучим модель с соответствующими параметрами, SARIMAX(3, 0, 0)x(0, 1, 0, 12) # импортируем класс модели from statsmodels.tsa.statespace.sarimax import SARIMAX # создадим объект этой модели model = SARIMAX(train, order = (3, 0, 0), seasonal_order = (0, 1, 0, 12)) # применим метод fit result = model.fit() |
Теперь мы готовы делать прогноз. Вначале сделаем тестовый прогноз, соответствующий периоду тестовой выборки (1960 год), для того, чтобы оценить качество работы модели.
|
1 2 3 4 5 6 7 8 9 |
# тестовый прогнозный период начнется с конца обучающего периода start = len(train) # и закончится в конце тестового end = len(train) + len(test) - 1 # применим метод predict predictions = result.predict(start, end) predictions |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
1960-01-01 422.703385 1960-02-01 404.947178 1960-03-01 466.293258 1960-04-01 454.781296 1960-05-01 476.848628 1960-06-01 527.162826 1960-07-01 601.449809 1960-08-01 610.821691 1960-09-01 513.229987 1960-10-01 455.692619 1960-11-01 409.200047 1960-12-01 450.754161 Freq: MS, Name: predicted_mean, dtype: float64 |
Построим соответствующий график.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# выведем три кривые (обучающая, тестовая выборка и тестовый прогноз) plt.plot(train, color = "black") plt.plot(test, color = "red") plt.plot(predictions, color = "green") # заголовок и подписи к осям plt.title("Обучающая выборка, тестовая выборка и тестовый прогноз") plt.ylabel('Количество пассажиров') plt.xlabel('Месяцы') # добавим сетку plt.grid() plt.show() |
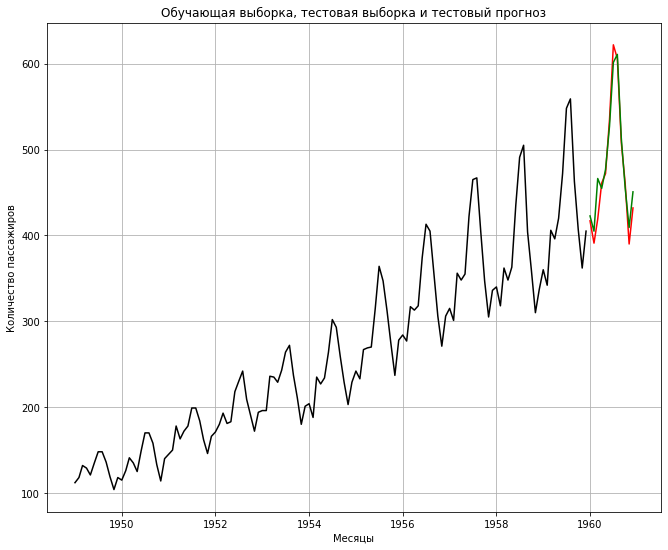
В целом модель хорошо описывает временной ряд. Мы также можем использовать знакомые нам метрики среднеквадратической ошибки (MSE) и корня среднеквадратической ошибки (RMSE) для оценки качества.
|
1 2 3 4 5 6 7 8 |
# импортируем метрику from sklearn.metrics import mean_squared_error # рассчитаем MSE print(mean_squared_error(test, predictions)) # и RMSE print(np.sqrt(mean_squared_error(test, predictions))) |
|
1 2 |
317.39565432961956 17.81560143047715 |
Теперь можно делать прогноз на будущее. Возьмём горизонт равный трем годам (1961, 1962 и 1963 год). Всего должно получиться 36 прогнозных значений.
|
1 2 3 4 5 6 7 8 9 10 11 |
# прогнозный период с конца имеющихся данных start = len(passengers) # и закончится 36 месяцев спустя end = (len(passengers) - 1) + 3 * 12 # теперь построим прогноз на три года вперед forecast = result.predict(start, end) # посмотрим на весь 1963 год forecast[-12:] |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
1963-01-01 518.603436 1963-02-01 497.908988 1963-03-01 556.406784 1963-04-01 542.133835 1963-05-01 561.524762 1963-06-01 609.244563 1963-07-01 681.016637 1963-08-01 687.950665 1963-09-01 587.995801 1963-10-01 528.167677 1963-11-01 479.454536 1963-12-01 518.856117 Freq: MS, Name: predicted_mean, dtype: float64 |
Посмотрим на прогнозные значения на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# выведем две кривые (фактические данные и прогноз на будущее) plt.plot(passengers, color = 'black') plt.plot(forecast, color = 'blue') # заголовок и подписи к осям plt.title('Фактические данные и прогноз на будущее') plt.ylabel('Количество пассажиров') plt.xlabel('Месяцы') # добавим сетку plt.grid() plt.show() |

Подведем итог
Занятие было насыщенным. Мы узнали, (1) чем временные ряды отличаются от структурных данных, (2) научились анализировать временные ряды с помощью Питона, а также (3) строить графики.
При прогнозировании временных рядов мы (4) использовали модель экспоненциального сглаживания и (5) познакомились с семейством моделей ARMA.
Вопросы для закрепления
Чем структурные/перекрестные данные отличаются от временных рядов?
Посмотреть правильный ответ
Ответ: во временных рядах значение наблюдаемой величины зависит от времени, в структурных данных — от других величин или переменных.
Что определяет параметр $ \alpha $ в модели экспоненциального сглаживания?
Посмотреть правильный ответ
Ответ: значение параметра $ \alpha $ близкое к единице повышает значимость текущего истинного наблюдения, если $ \alpha $ близка к нулю — превалирует предыдущее прогнозное значение.
Из каких компонентов состоит модель ARMA?
Посмотреть правильный ответ
Ответ: модель ARMA состоит из компонента авторегрессии (AR), т.е. регрессии на собственные значения в прошлом, и модели скользящего среднего (MA), учитывающей отклонение от среднего значения или ошибку.
В рамках вводного курса осталась одна тема, основы нейронных сетей.
Ответы на вопросы
Вопрос. Вы не могли бы более детально рассказать, как подбираются параметры в модели SARIMAX. В частности, как были подобраны параметры (3, 0, 0)x(0, 1, 0, 12)?
Ответ. Параметры SARIMAX можно подобрать с помощью функции auto_arima. Выбор наиболее удачных параметров осуществляется на основе определенного критерия.
По умолчанию используется, так называемый, Akaike Information Criterion или AIC, который рассчитывается для каждой комбинации параметров. Чем ниже AIC модели, тем лучше.
Я привел код auto_arima в конце ноутбука⧉.
Вопрос. У меня уточнение: скажите, там, где мы считаем экспоненциальное сглаживание,
|
1 2 3 |
# в цикле for последовательно применяем формулу ко всем элементам ряда for i in range(0, len(births['Births'])): exp_smoothing.append(alpha * births['Births'][i] + (1 - alpha) * exp_smoothing[i - 1]) |
там, может быть, нужно в цикле for i in range(0, len(births['Births'])): поставить начальное значение счетчика = 1: for i in range(1, len(births['Births']))?
Я проверял выкладки в Экселе — и, когда цикл стартует с нуля, получается ошибка. Возможно, это потому, что в начале списка получается задублированное значение первого элемента (мы сначала вручную вносим в список [births['Births'][0]], а потом это же делаем на первой итерации, когда значение счетчика = 0)
Ответ. Да, действительно, первое прогнозное значение мы вносим вручную (оно совпадает с первым фактическим значением), поэтому должно быть
|
1 |
for i in range(1, len(births['Births'])): |
Внес изменения в ноутбук и текст лекции.