Все курсы > Вводный курс > Занятие 17
Что такое рекомендательная система?
Рекомендательная система (recommender system) стремится максимально точно предсказать предпочтения потребителя и предложить наиболее подходящий товар или услугу.
Сегодня такие системы встречаются повсеместно. Практически любой крупный интернет-магазин, онлайн-кинотеатр или новостной портал использует ту или иную рекомендательную систему для того, чтобы предоставить пользователям то, что им действительно нужно.
На этом занятии мы коротко рассмотрим основные типы рекомендательных систем, а затем создадим свою рекомендательную систему для онлайн-кинотеатра. Итак, начнем.
Типы рекомендательных систем
Для простоты выделим три типа рекомендательных систем: фильтрация по популярности, на основе содержания и коллаборативная система.

Наиболее простая система выдает рекомендации на основе популярности (popularity-based recommender systems). Чем выше средний рейтинг фильма, купленного товара или статьи, тем вероятнее, что система будет рекомендовать именно их.
Преимуществом является простота, недостатком то, что не учитываются предпочтения конкретного пользователя.
Вторым типом рекомендательных систем является, так называемая, фильтрация на основе содержания (content-based filtering). В данном случае алгоритм рекомендует товары или услуги, схожие с теми, которые пользователь приобретал ранее. Например, если вы посмотрели фильм «Матрица» с Киану Ривзом, то в дальнейшем система будет рекомендовать вам научную фантастику, а также другие фильмы с участием этого актера.
Такую систему также несложно реализовать, при этом основным недостатком будет то, что покупатели не пробуют новые товары или услуги.
Третий тип — коллаборативная система (collaborative filtering). Именно ей мы и будем сегодня заниматься. Она основывается на сопоставлении пользователей и товаров (или услуг, новостей и т.д.). Математически и графически в данном случае мы работаем с матрицами предпочтений (user-item matrix).

Существует два вида таких систем.
Коллаборативные системы, основанные на пользователях (user-based), находят близких по предпочтениям пользователей и рекомендуют одному из них то, что уже попробовал другой.
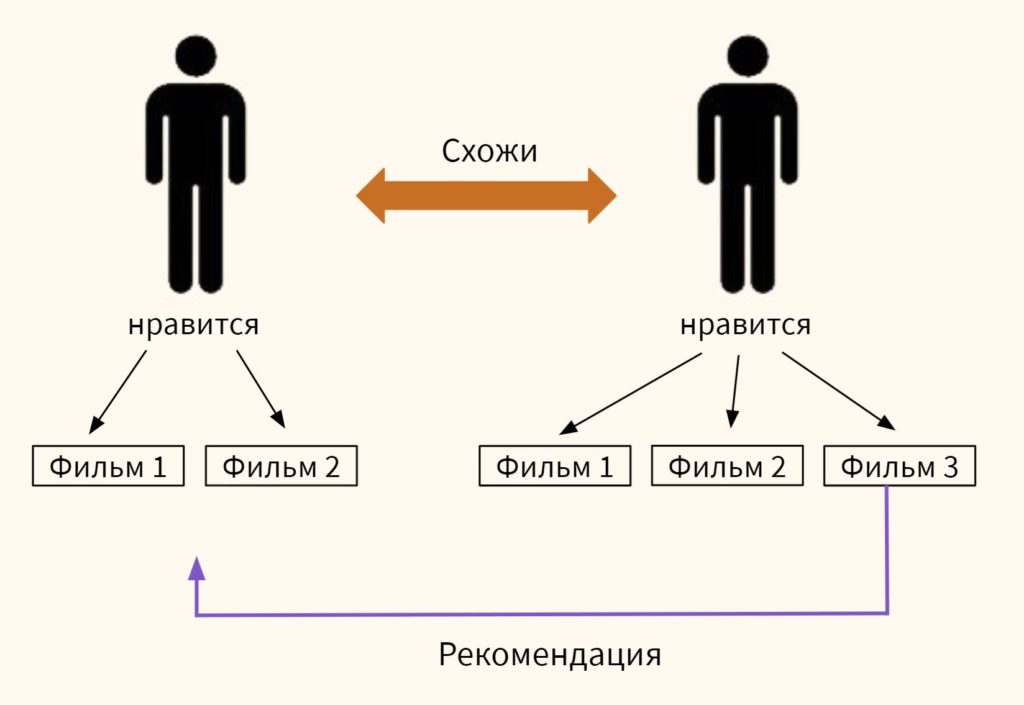

Системы, основанные на предмете рекомендации (item-based), сравнивают непосредственно близость товаров или услуг. Причем что отличает эту систему, сходство определяется на основе предпочтений всех пользователей, которые оставили свои оценки.
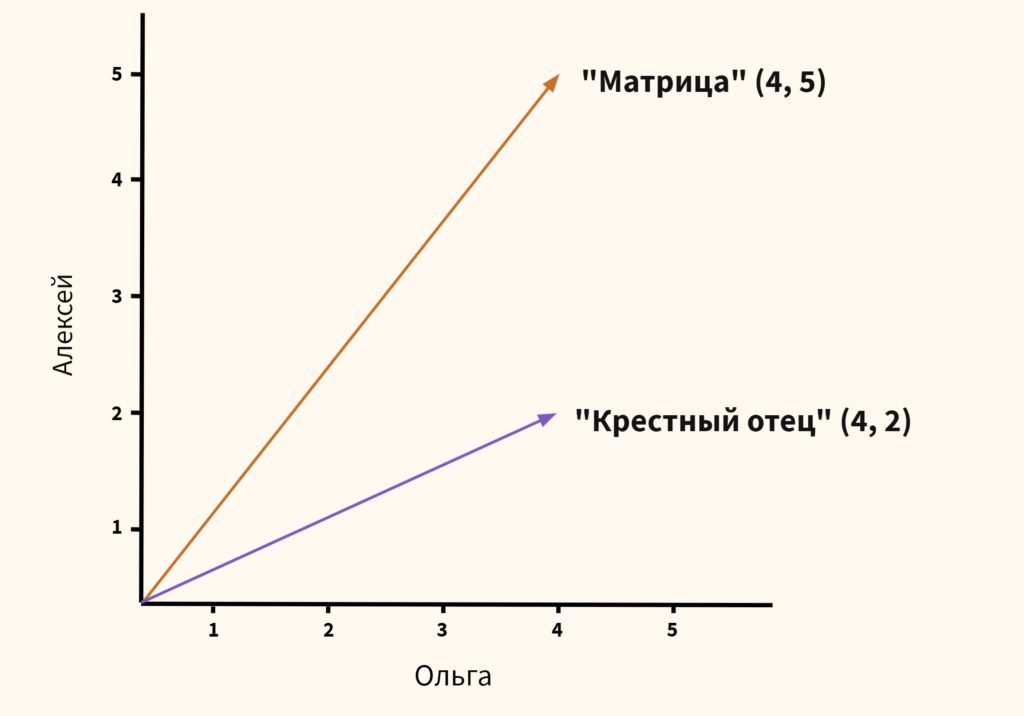
Как вы вероятно догадались, мы будем использовать косинусное сходство для оценки расстояния.
Рекомендательная система для онлайн-кинотеатра
Теперь давайте пошагово обсудим, что нам предстоит сделать.
На этом занятии мы будем создавать коллаборативную систему, основанную на предмете рекомендации (item-based collaborative filtering recommender system). Впервые она была разработана компанией Amazon в 1998 году.
Итак, на первом этапе, нам нужно подготовить данные, то есть создать матрицу предпочтений, где строками будут фильмы, столбцами — пользователи, а элементами — рейтинги.
На втором этапе, мы рассчитаем расстояния от каждого фильма до ближайших векторов (других фильмов).
Для этого мы будем использовать алгоритм k-ближайших соседей (k-nearest neighbors algorithm, k-NN). Графически его работа выглядит следующим образом.

На третьем этапе, возьмем картину, для которой хотим подобрать рекомендации, и найдем в базе данных фильмы с наибольшим косинусным сходством.
В частности, предлагаю взять уже упомянутый фильм «Матрица» и посмотреть, предложит ли такая система фильмы с Киану Ривзом или научную фантастику.
Практика
Мы воспользуемся открытым набором данных о рейтинге фильмов MovieLens Latest Datasets. В этом датасете, в частности, содержатся названия фильмов (файл movies.csv) и оценки, которые фильмам ставили зрители (файл rating.csv).
Теперь откроем ноутбук к этому занятию⧉
Этап 1. Подготовка данных
Я предполагаю, что вы уже скачали оба файла на свой компьютер. Теперь их нужно подгрузить в ноутбук. Это можно сделать открыв вкладку «Файлы» в меню слева и выбрав значок «Загрузить в сессионное хранилище».
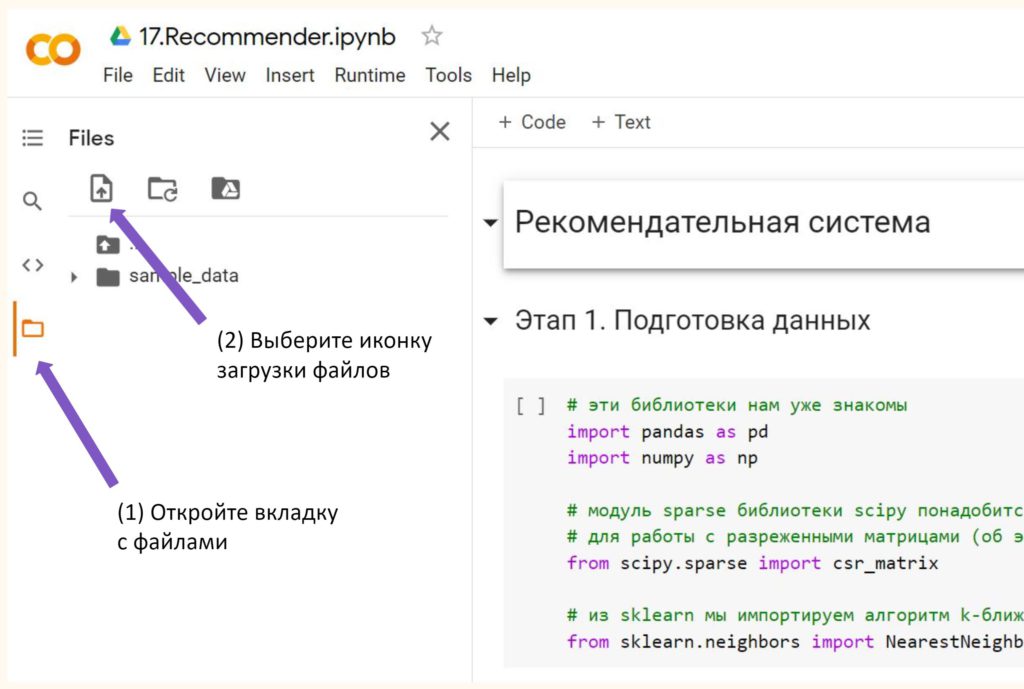

Обратите внимание, файлы хранятся в памяти временно и их придется подгружать каждый раз при перезапуске рабочей среды. Я выбрал этот способ подгрузки внешних данных из-за его простоты.
Теперь мы готовы использовать эти файлы для создания рекомендательной системы. В первую очередь, импортируем необходимые библиотеки.
|
1 2 3 4 5 6 7 8 9 10 |
# эти библиотеки нам уже знакомы import pandas as pd import numpy as np # модуль sparse библиотеки scipy понадобится # для работы с разреженными матрицами (об этом ниже) from scipy.sparse import csr_matrix # из sklearn мы импортируем алгоритм k-ближайших соседей from sklearn.neighbors import NearestNeighbors |
Теперь нам нужно импортировать наши файлы movies.csv и rating.csv и преобразовать их в датафреймы. Для этого мы будем использовать функцию read_csv библиотеки Pandas.
|
1 2 |
movies = pd.read_csv('/content/movies.csv') ratings = pd.read_csv('/content/ratings.csv') |
Информация в этим файлах записана в формате .csv или comma-separated values, это значит, что значения одной строки просто разделены запятыми.
|
1 2 3 4 5 |
# посмотрим на содержимое файла movies.csv # дополнительно удалим столбец genres, он нам не нужен # (параметр axis = 1 говорит, что мы работаем со столбцами, inplace = True, что изменения нужно сохранить) movies.drop(['genres'], axis = 1, inplace = True) movies.head(3) |

|
1 2 3 |
# и ratings.csv (здесь также удаляем ненужный столбец timestamp) ratings.drop(['timestamp'], axis = 1, inplace = True) ratings.head(3) |

Теперь нам необходимо создать матрицу предпочтений. Для этого мы воспользуемся сводной таблицей (pivot table). В библиотеке Pandas такую таблицу можно создать, в частности, с помощью функции
|
1 2 3 |
# по горизонтали будут фильмы, по вертикали - пользователи, значения - оценки user_item_matrix = ratings.pivot(index = 'movieId', columns = 'userId', values = 'rating') user_item_matrix.head() |

NaN расшифровывается как Not A Number и представляет собой наиболее частый способ отображения пропущенных значений. Так как мы будем заниматься вычислениями расстояния, каждое значение таблицы должно быть числовым. С помощью функции fillna() мы заменим NaN на ноль.
|
1 2 3 |
# параметр inplace = True опять же поможет сохранить результат user_item_matrix.fillna(0, inplace = True) user_item_matrix.head() |
Замена пропущенных значений (imputation of missing values) — это сам по себе довольно сложный и интересный процесс, ведь далеко не всегда можно заменить пропуски нулями.

Теперь давайте уберем неактивных пользователей и фильмы с небольшим количеством оценок. С одной стороны, такие пользователи не окажут существенного влияния на расстояния между фильмами, с другой, малому количеству оценок довольно сложно доверять.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# вначале сгруппируем (объединим) пользователей, возьмем только столбец rating # и посчитаем, сколько было оценок у каждого пользователя users_votes = ratings.groupby('userId')['rating'].agg('count') # сделаем то же самое, только для фильма movies_votes = ratings.groupby('movieId')['rating'].agg('count') # теперь создадим фильтр (mask) user_mask = users_votes[users_votes > 50].index movie_mask = movies_votes[movies_votes > 10].index # применим фильтры и отберем фильмы с достаточным количеством оценок user_item_matrix = user_item_matrix.loc[movie_mask,:] # а также активных пользователей user_item_matrix = user_item_matrix.loc[:,user_mask] |
Теперь давайте посмотрим на новую размерность, то есть на те фильмы и тех пользователей, которые остались после фильтрации данных.
|
1 |
user_item_matrix.shape |
|
1 |
(2121, 378) |
Про разреженные матрицы и высокую размерность
В нашем датасете по понятным причинам очень много нулей. Такая матрица называется разреженной (sparse matrix). Одновременно, если столбцов очень много (а у нас их уже довольно много), то говорят про данные с высокой размерностью (high-dimensional data). В таком формате алгоритм будет долго обсчитывать расстояния между фильмами.
Для того, чтобы преодолеть эту сложность можно преобразовать данные в формат сжатого хранения строкой (сompressed sparse row, csr).
|
1 2 |
# атрибут values передаст функции csr_matrix только значения датафрейма csr_data = csr_matrix(user_item_matrix.values) |
Посмотрим на результат.
|
1 |
print(csr_data[:2,:5]) |
|
1 2 3 |
(0, 0) 4.0 (0, 3) 4.5 (1, 2) 4.0 |
Как мы видим в таком формате в каждой строке сначала записывается номер строки и стобца ненулевого значения, а затем само это значение. Если взять исходный датафрейм, то по этой кодировке будет нетрудно найти ненулевые значения.
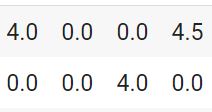
Остается только сбросить индекс для удобства поиска рекомендованных фильмов.
|
1 2 |
user_item_matrix = user_item_matrix.rename_axis(None, axis = 1).reset_index() user_item_matrix.head() |

Обратите внимание, фильм с movieId == 4 не прошел фильтры и не включен в наш датасет. Также в него не вошли, например, второй и третий пользователи. Все, данные готовы для обучения модели.
Этап 2. Обучение модели
Как уже было сказано, для обучения модели мы будем использовать алгоритм k-ближайших соседей. Этот алгоритм решает разные задачи, в частности, с его помощью можно заниматься регрессией (класс KNeighborsRegressor) и классификацией (класс KNeighborsClassifier).
Для наших целей нам достаточно измерить расстояние между объектами. В этом нам поможет класс машинного обучения без учителя NearestNeighbors.
|
1 2 3 4 5 6 7 8 |
# создадим объект класса NearestNeighbors knn = NearestNeighbors(metric = 'cosine', algorithm = 'brute', n_neighbors = 20, n_jobs = -1) # обучим модель knn.fit(csr_data) |
Теперь давайте подробнее поговорим про параметры:
- metric = ‘cosine’: выбираем способ измерения расстояния, в нашем случае это будет косинусное сходство
- algorithm = ‘brute’: предполагает, что мы будем искать решение методом полного перебора (brute force search), в данном случае пространство решений позволяет перебрать все варианты
- n_neighbors = 20: по скольким соседям ведется обучение
- n_jobs = -1: в этом случае предполагается, что вычисления будут вестись на всех свободных ядрах процессора
Итак, мы готовы рекомендовать кино для просмотра.
Этап 3. Составление рекомендаций
Введем изначальные параметры: количество рекомендаций и на основе какого фильма мы их хотим получить (мы говорили о том, что будем смотреть на рекомендации для «Матрицы»).
|
1 2 |
recommendations = 10 search_word = 'Matrix' |
Теперь найдем индекс фильма в матрице предпочтений.
|
1 2 3 |
# для начала найдем фильм в заголовках датафрейма movies movie_search = movies[movies['title'].str.contains(search_word)] movie_search |

|
1 2 3 4 5 6 7 8 |
# вариантов может быть несколько, для простоты всегда будем брать первый вариант # через iloc[0] мы берем первую строку столбца ['movieId'] movie_id = movie_search.iloc[0]['movieId'] # далее по индексу фильма в датасете movies найдем соответствующий индекс # в матрице предпочтений movie_id = user_item_matrix[user_item_matrix['movieId'] == movie_id].index[0] movie_id |
|
1 |
901 |
Это индекс фильма в матрице предпочтений (после того как мы сбросили индекс). Далее с помощью метода .kneighbors() найдем индексы ближайших соседей «Матрицы».
|
1 |
distances, indices = knn.kneighbors(csr_data[movie_id], n_neighbors = recommendations + 1) |
В качестве параметров мы передадим:
- csr_data[movie_id], то есть индекс нужного нам фильма из матрицы предпочтений в формате сжатого хранения строкой
- n_neighbors, количество соседей (или рекомендаций); обратите внимание, мы добавляем «лишнего» соседа (+1) из-за того, что алгоритм также считает расстояние до самого себя
На выходе мы получаем массив индексов фильмов (indices) и массив расстояний (distances) до них. Для удобства преобразуем эти массивы в списки, а затем попарно объединим и создадим кортежи (tuples).
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# уберем лишние измерения через squeeze() и преобразуем массивы в списки с помощью tolist() indices_list = indices.squeeze().tolist() distances_list = distances.squeeze().tolist() # далее с помощью функций zip и list преобразуем наши списки indices_distances = list(zip(indices_list, distances_list)) # в набор кортежей (tuple) print(type(indices_distances[0])) # и посмотрим на первые три пары/кортежа print(indices_distances[:3]) |
|
1 2 |
<class 'tuple'> [(901, 0.0), (1002, 0.22982440568634488), (442, 0.25401128310081567)] |
|
1 2 3 4 5 6 7 |
# остается отсортировать список по расстояниям через key = lambda x: x[1] (то есть по второму элементу) # в возрастающем порядке reverse = False indices_distances_sorted = sorted(indices_distances, key = lambda x: x[1], reverse = False) # и убрать первый элемент с индексом 901 (потому что это и есть "Матрица") indices_distances_sorted = indices_distances_sorted[1:] indices_distances_sorted |
|
1 2 3 4 5 6 7 8 9 10 |
[(1002, 0.22982440568634488), (442, 0.25401128310081567), (454, 0.27565616686043737), (124, 0.2776088577731709), (735, 0.2869100842838125), (954, 0.2911101181714415), (1362, 0.31393358217709477), (1157, 0.31405925934381695), (1536, 0.3154800434449465), (978, 0.31748544046311844)] |
Итак, индексы у нас есть. Теперь нужно найти какие фильмы (вернее их названия) им соответствуют. Для этого обратимся к датафрейму movies.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# создаем пустой список, в который будем помещать название фильма и расстояние до него recom_list = [] # теперь в цикле будем поочередно проходить по кортежам for ind_dist in indices_distances_sorted: # искать movieId в матрице предпочтений matrix_movie_id = user_item_matrix.iloc[ind_dist[0]]['movieId'] # выяснять индекс этого фильма в датафрейме movies id = movies[movies['movieId'] == matrix_movie_id].index # брать название фильма и расстояние до него title = movies.iloc[id]['title'].values[0] dist = ind_dist[1] # помещать каждую пару в питоновский словарь # который, в свою очередь, станет элементом списка recom_list recom_list.append({'Title' : title, 'Distance' : dist}) |
Посмотрим на первый элемент получившегося списка:
|
1 |
recom_list[0] |
|
1 |
{'Title': 'Fight Club (1999)', 'Distance': 0.22982440568634488} |
Остается преобразовать наш список в датафрейм.
|
1 2 3 |
# индекс будем начинать с 1, как и положено рейтингу recom_df = pd.DataFrame(recom_list, index = range(1, recommendations + 1)) recom_df |

В некоторых случаях результат может показаться неожиданным, однако важно помнить, что мы учитываем предпочтения всех пользователей, а значит наши представления о схожести фильмов не обязательно являются верными (скорее даже наоборот).
Работа над ошибками. На видео в коде есть ошибка.
|
1 2 3 |
indices_distances_sorted = sorted(indices_distances, key = lambda x: x[1], reverse = True) indices_distances_sorted = indices_distances_sorted[:-1] indices_distances_sorted |
При сортировке фильмов по расстоянию указан параметр reverse = True, то есть в убывающем порядке. Из-за этого на первом месте рейтинга из десяти рекомендованных фильмов оказались картины с наибольшим расстоянием от искомого фильма.

На сайте и в ноутбуке ошибка исправлена.
Подведем итог
Сегодня мы создали коллаборативную рекомендательную систему, которая предлагает фильмы на основе предпочтений пользователей.
Вопросы для закрепления
Какие типы рекомендательных систем вы знаете?
Посмотреть правильный ответ
Ответ: на сегодняшнем занятии мы узнали про рекомендательные системы на основе популярности, содержания, а также про коллаборативную систему.
В чем заключается основное отличие двух видов коллаборативных систем?
Посмотреть правильный ответ
Ответ: система, основанная на пользователях (user-based), сравнивает векторы пользователей, система, основанная на предмете рекомендации (item-based), сравнивает схожесть товаров, услуг или контента.
Что такое разреженная матрица (sparse matrix)?
Посмотреть правильный ответ
Ответ: в разреженной матрице большая часть элементов равна нулю.
На следующем занятии мы займемся работой с изображениями.
Ответы на вопросы в комментариях
Вопрос. Если одному фильму все пользователи поставили по 10 баллов, а второму фильму — по одному баллу, то правильно ли я понимаю, что между векторами этих фильмов будет нулевой угол. И если пришел новый пользователь, который поставил первому фильму 10 баллов, то система порекомендует ему второй фильм (чего с точки зрения логики быть не должно)?
Ответ. (1) На первую часть вопроса, ответ «да», угол будет нулевой, потому что векторы коллинеарны (т.е. лежат на одной прямой или на параллельных прямых) и сонаправлены, различается только их длина.
Для вектора с двумя координатами это легко увидеть на графике.
|
1 2 |
import numpy as np import matplotlib.pyplot as plt |
|
1 2 3 |
# создадим два вектора с координатами [10, 10] и [1, 1] x = np.array([10, 10]) y = np.array([1, 1]) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# зададим размер фигуры (контейнера, в который помещаются графики) plt.figure(figsize = (10, 6)) # создадим объект графика внутри этой фигуры ax = plt.axes() # зададим диапазон осей x и y plt.xlim([0, 11]) plt.ylim([0, 11]) plt.grid() # нашими "подграфиками" будут два вектора в форме стрелок ax.arrow(0, 0, x[0], x[1], width = 0.03, head_width = 0.2, head_length = 0.2, fc = 'g', ec = 'g') ax.arrow(0, 0, y[0], y[1], width = 0.03, head_width = 0.2, head_length = 0.2, fc = 'b', ec = 'b') plt.show() |

Примечание: про создание графиков в Matplotlib мы подробно поговорим на курсе по анализу данных.
Можно также рассчитать косинусное сходство.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# напишем функцию для расчета косинусного сходства def similar(x, y): # рассчитаем длины векторов xLen = np.linalg.norm(x) yLen = np.linalg.norm(y) # подставим их в формулу косинусного сходства result = np.dot(x, y)/(xLen * yLen) # выведем результат return result |
|
1 2 |
# ожидаемо косунус угла между коллинеарными векторами будет равен единице round(similar(x, y), 3) |
|
1 |
1.0 |
Примечание: про создание функций можно посмотреть здесь.
(2) Со второй частью вопроса, я бы вначале несколько переформулировал его, потому что если у нас есть два фильма, которым все пользователи ставят рейтинги 10 и 1 соответственно, то мы сравниваем фильмы, а не пользователей (а значит это item-based, а не user-based система).
Как следствие, нужно посмотреть, что будет, если появится новый фильм, которому пользователи поставят оценки в 10 баллов. И вот здесь возникает справедливый вопрос, к какому из уже имеющихся в системе фильмов будет близок новый фильм с этими рейтингами?
Для решения этой задачи давайте построим простейшую item-based систему. Возьмем пять фильмов, пусть трем из них пользователи поставят разные оценки, а двум другим — только десятки и только единицы.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# создадим массив Numpy с оценками films = np.array( [ [1, 3, 2, 6, 2, 1, 0], [0, 2, 0, 3, 0, 6, 2], [1, 1, 1, 1, 1, 1, 1], [2, 4, 1, 3, 9, 2, 1], [10, 10, 10, 10, 10, 10, 10] ] ) # строки это фильмы, столбцы - пользователи films |
|
1 2 3 4 5 |
array([[ 1, 3, 2, 6, 2, 1, 0], [ 0, 2, 0, 3, 0, 6, 2], [ 1, 1, 1, 1, 1, 1, 1], [ 2, 4, 1, 3, 9, 2, 1], [10, 10, 10, 10, 10, 10, 10]]) |
Предположим, вышел новый фильм, и все пользователи поставили ему рейтинг 10.
|
1 |
new_film = np.array([10, 10, 10, 10, 10, 10, 10]) |
В цикле for поочередно рассчитаем косинусное сходство каждого из имеющихся фильмов с новым фильмом.
|
1 2 3 |
# для этого снова воспользуемся функцией similar() for i, film in enumerate(films, 1): print(f'Фильм {i} с оценками {film} имеет сходство с новым фильмом {np.round(similar(film, new_film), 3)}') |
|
1 2 3 4 5 |
Фильм 1 с оценками [1 3 2 6 2 1 0] имеет сходство с новым фильмом 0.764 Фильм 2 с оценками [0 2 0 3 0 6 2] имеет сходство с новым фильмом 0.675 Фильм 3 с оценками [1 1 1 1 1 1 1] имеет сходство с новым фильмом 1.0 Фильм 4 с оценками [2 4 1 3 9 2 1] имеет сходство с новым фильмом 0.772 Фильм 5 с оценками [10 10 10 10 10 10 10] имеет сходство с новым фильмом 1.0 |
Как мы видим, система показала, что новый фильм одинаково близок как к фильму с рейтингами 1 от всех пользователей, так и к фильму с рейтингами 10. Конечно, это противоречит здравому смыслу.
На практике такая ситуация маловероятна, потому что мы работаем с матрицами с огромным количеством пользователей и фильмов. Вряд ли все пользователи поставят фильму одни и те же оценки. Однако в целом да, при создании коллаборативных систем возникает ряд сложностей.
О некоторых сложностях создания коллаборативных систем
Например, есть проблема разреженности (sparcity) матрицы предпочтений, когда многие пользователи не оставляют оценок, матрица заполняется нулями и от этого страдает качество рекомедаций (мы с этим столкнулись, в частности, в нашей учебной модели).
Кроме того, существует проблема холодного старта (cold start), когда либо (1) в системе в самом начале ее работы недостаточно данных для генерации рекомендаций, либо (2) пришел новый пользователь, который еще не ставил оценок, и система не знает, что ему посоветовать, либо (3) вышел новый фильм, книга, товар, которые пока не имеют рейтингов, и их схожесть с другими предметами рекомендации не так просто рассчитать.
Помимо этого, появление новых пользователей и новых фильмов вынуждают производить перерасчет расстояний в системе. Это всегда затратно с точки зрения вычислительных мощностей. В этом смысле, item-based система более удобна, чем user-based система, потому что фильмы, например, добавляются в систему реже, чем пользователи.
Весь код, приведенный в ответе, можно найти в конце ноутбука⧉.
Вопрос. Скажите можно ли разделить выборку на обучающую и тестовую? И если да, может подскажете в комментарии как?
Ответ. Один из подходов — использовать leave one out cross validation в качестве метода разделения данных и RMSE или MAE в качестве метрики качества алгоритма.
В этом случае один из рейтингов изымается из набора данных и становится тестовой выборкой, остальные рейтинги соответственно остаются в обучающей. Алгоритм обучается на имеющихся данных и делает прогноз для того рейтинга, который мы изъяли. Далее рассчитывается RMSE (который сравнивает прогнозное значение с фактическим).
Процесс повторяется для остальных рейтингов и затем рассчитывается средний RMSE по всем итерациям.
Для того чтобы сократить время вычислений, за одну итерацию можно брать не один, а несколько рейтингов, то есть использовать leave n-out cross validation.