Взаимосвязь переменных

Все курсы > Вводный курс > Занятие 10

На восьмом занятии мы рассмотрели качественные и количественные переменные. Однако мы изучали их изолированно, каждую переменную отдельно.

На самом деле переменные могут быть связаны между собой. И эту взаимосвязь очень интересно изучать. Рассмотрим несколько примеров.

Вначале откроем ноутбук к этому занятию⧉

Пример: рост мужчин и женщин в России

Вначале продолжим пример с ростом, однако теперь введем ещё одну переменную, пол, и посмотрим, повляет ли это на распределение данных.

Создадим две гистограммы.

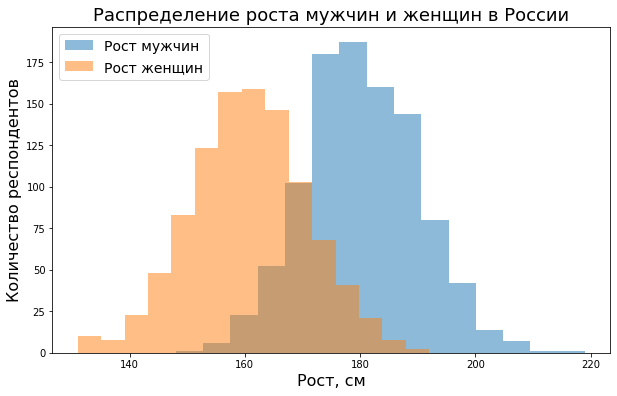
В данном случае мы видим, что если мы разделим людей на мужчин и женщин, распределение их роста не будет одинаковым. Средний рост у них разный.

Аналогичным образом, мы можем посмотреть на взаимосвязь двух количественных переменных. Например, посмотрим, как меняется обхват шеи человека с увеличением роста.

Пример: рост женщин и окружность их шеи

Для этого нам надо построить новый для нас тип графика: диаграмму рассеяния или точечную диаграмму (scatter plot). Каждая точка на графике — одно наблюдение.

Как мы видим, с увеличением роста окружность шеи увеличивается.

Пусть вас не пугает многообразие диаграмм. Со временем и практикой вы будете прекрасно в них ориентироваться.

Корреляция

Степень взаимосвязи переменных можно измерить.

Для двух количественных переменных можно воспользоваться коэффициентом Пирсона. Диапазон значений этого коэффициента находится в пределах от минус единицы (отрицательная корреляция, если один показатель увеличивается, другой уменьшается и наоборот) до плюс единицы (положительная корреляция, если один увеличивается, другой тоже увеличивается и наоборот). Ноль означает отсутствие корреляции.

Ниже приведены графические примеры возможных корреляций.

Рассчитаем коэффициент корреляции с помощью Питона.

Результат:

Очень высокая, почти идеальная положительная корреляция.

Напомню, что даже корреляция равная единице или минус единице не означает наличие причинно-следственной связи.

Идем дальше. Ровно так как мы можем с определенной долей уверенности сделать вывод о генеральной совокупности по выборке, точно также мы можем смоделировать взаимосвязь переменных по ограниченному набору данных.

Построение модели

Рассмотрим модель, которую называют моделью линейной регрессии, и попробуем с ее помощью математически описать связь роста и обхвата шеи.

Модель линейной регрессии

Вначале напомню, что линия на графике описывается знакомым нам уравнением вида

$$ y = w \times x + b $$

где w и b — это веса и одновременно наклон и сдвиг прямой вверх или вниз.

Теперь возьмем имеющиеся у нас данные и проведем через них линию, но не случайным образом, а так, чтобы сумма расстояний от этой прямой до точек было минимальным. Воспользуемся Питоном.

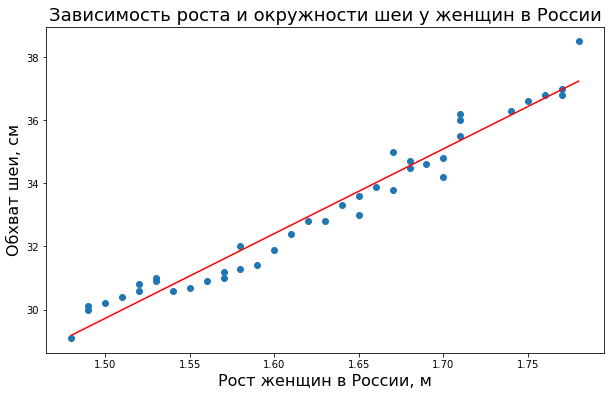
Теперь посмотрим на то, какой наклон и сдвиг нашел для нас Питон.

Подставим полученные значения вместо w и e в уже известное нам выражение, чтобы найти уравнение именно этой прямой.

$$ y = 26.86x-10.57 $$

Предсказание роста

Модель готова делать прогноз. Предположим, нам встретилась еще одна девушка, и ее рост составляет 1,73 м. Каким будет обхват ее шеи? Подставим рост нового респондента в уравнение вместо независимой переменной x.

Результат:

Напоследок замечу, что для прогнозных значений также можно задавать доверительный интервал, ровно так, как мы это делали для среднего генеральной совокупности на прошлом занятии.

Граница между статистикой и машинным обучением

Внимательный читатель скажет, что регрессионный анализ, то есть построение модели регрессии, также является разделом статистики и не относится исключительно к области машинного обучения.

В рамках настоящего курса, для простоты и системности изложения я буду рассматривать регрессию только как одну из моделей машинного обучения.

Подведем итог

На этом занятии мы узнали, что между переменными может существовать взаимосвязь. Если одна переменная категориальная, а другая — количественная, их удобно изобразить с помощью двух гистограмм, расположенных на одном графике. Если обе количественные — подойдет точечная диаграмма.

Кроме того, если мы хотим математически описать наши данные, то можем построить модель. Например, модель линейной регрессии, которая графически представляет собой прямую линию, проходящую через данные.

Алгебраически, прямая описывается уравнением $$ y = w \times x + b $$

Вопросы для закрепления

Корреляция двух количественных величин равна −0.8. Как интерпретировать этот коэффициент?

Что определяют веса w и b на графике?

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

Нахождение весов

В наших рассуждениях все ещё остаётся один не проясненный момент: как мы нашли w и b? Именно этим вопросом мы и начнем заниматься на следующем занятии, посвященном оптимизации.

---

Вопрос и комментарии

Комментарий. При визуальном сравнении двух выборок с помощью гистограмм могут возникнут сложности, если выборки сильно различаются по размерам. Одна гистограмма может оказаться значительно ниже другой, сожмётся и на ней сложно будет оценить распределение и среднее.

Выборки разного размера удобно сравнивать с помощью боксплотов, которые не учитывают размеры выборок, но зато позволяют оценить, как они соотносятся между собой по медианам, размахам, квартилям.

Также на графике с боксплотами удобно сравнивать выборки, когда их больше двух. График с гистограммами в таком случае станет совсем тяжелым для чтения.

Ответ. Полностью согласен. Все это рассмотрим на курсе по анализу данных.

На вводном курсе я сознательно опустил некоторые разделы, чтобы не перегружать информацией тех, кто первый раз знакомится со статистикой.

На данном этапе мне важно, чтобы был виден переход от анализа данных и выявления взаимосвязи между переменными к построению модели.