Регуляризация модели

Все курсы > Оптимизация > Занятие 7

В рамках вводного курса мы подробно обсудили вопрос разделения выборки на обучающую и тестовую части, а также затронули проблему переобучения и недообучения модели. Рассмотрим этот вопрос более подробно.

Переобучение и недообучение модели

Переобучение (overfitting) случается, когда модель показывает хороший результат на обучающей выборке и сильно «проседает» на тестовых данных. При недообучении (underfitting) наоборот у алгоритма не получается уловить зависимость на обучающих данных.

Вспомним график из вводного курса.

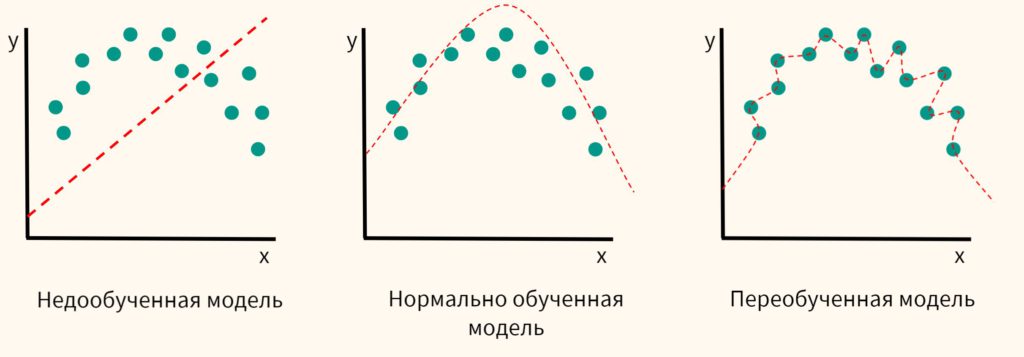
Дополним его для наглядности иллюстрацией того, как может повести себя переобученная модель на тестовых данных.

Также рассмотрим пример переобучения и недообучения в задаче классификации.

С точки зрения уровня ошибки на обучающих и тестовых данных можно привести следующий график. Предположим, что мы взяли полиномиальную регрессию и смотрим на значение функции потерь на обучающих и тестовых данных для различных степеней регрессии.

Как вы видите, после определенной границы сложности модели ошибка на тестовых данных начала расти. Рассмотрим этот вопрос под разными углами и введем несколько новых терминов.

Сложность модели

Причиной пере- и недообучения может быть степень сложности используемой модели (model complexity). Под сложностью в данном случае понимается тип или типы используемых алгоритмов, способность к выявлению линейных или нелинейных зависимостей, количество рассматриваемых признаков и другие факторы.

В целом, можно сказать, что более простая модель склонна к недообучению, более сложная — к переобучению.

Например, полиномиальная модель (особенно с полиномом высокой степени) зачастую способна уловить более сложную зависимость, чем модель линейной регрессии. Если модель хорошо описывает исходные данные, говорят, что у нее низкое смещение.

Смещение

Cмещение (bias) означает матожидание разности между истинным и прогнозным значением.

$$ Bias = E [\hat{y}-y] $$

Другими словами, смещение показывает, насколько хорошо модель обучилась на имеющихся данных (настроилась на выборку). Впрочем, как мы уже сказали в самом начале, идеально обученная (переобученная) модель может иметь минимальное смещение и при этом показать слабые результаты на тестовых данных. В этом случае говорят о большом разбросе.

Разброс

Разброс (variance) показывает насколько результат модели на обучающей выборке отличается от результата модели на тестовой выборке. То есть предсказания на тесте (например, на нескольких выборках) имеют разброс, и нам важно чтобы эти результаты не слишком отличались (тогда можно сказать, что у модели хорошая обобщающая способность).

Компромисс смещения и разброса

На практике стремление к снижению смещения может привести к увеличению разброса, т.е. переобучению, и, наоборот, высокое смещение модели может способствовать низкому разбросу, но смысла в этом не будет, потому что модель будет недообучена.

Эту проблему принято называть компромиссом или дилеммой смещения и разброса (bias-variance tradeoff). Посмотрим на рисунок ниже.

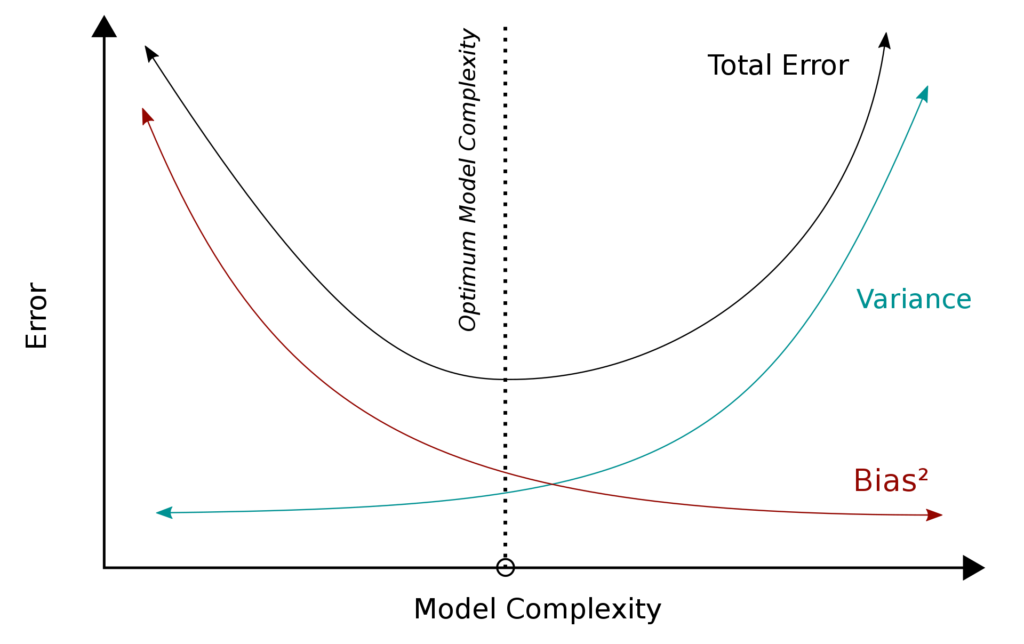
Рассмотрим еще одну полезную для понимания смещения и разброса иллюстрацию. На левом графике изобразим модели (каждая точка на графике — это прогноз одной модели), которые не очень хорошо описывают данные. Например, представим, что мы пытаемся описать полиномом первой степени зависимость, которая гораздо лучше описывается с помощью квадратичной функции.

Оценим прогнозы этих моделей в условной точке x = 5.

Коричневым цветом обозначены те «правильные» ответы, которые мы хотели бы получить. Свести их в одну точку мы не можем, потому что даже в идеальном случае мы можем получить прогноз с точностью до шума (случайных колебаний). Bias (фиолетовая стрелка) отражает ошибку, связанную с тем, что мы ошиблись с выбором модели (степень полинома). Разброс (зеленый цвет) — прогнозы моделей на нескольких обучающих выборках.

На правом графике, благодаря правильно подобранным (например, полином второй степени, снижает bias) и хорошо настроенным (снижает variance) моделям мы смогли существенно улучшить качество ответов.

Математика

Выразим три упомянутых компонента (смещение, разброс/дисперсия, шум) математически. Изначально мы хотим предсказать следующую зависимость.

$$ \hat{f}(X) = f(X) + \varepsilon, \varepsilon \sim N(0, \sigma_{\varepsilon}) $$

Ошибка в точке x равна

$$ Err(x) = E[(Y-\hat{f}(x))^2] $$

Ошибку можно разложить на

$$ Err(x) = \left( E[\hat{f}(x)]-f(x) \right)^2 + E \left[ \left( \hat{f}(x)-E[\hat{f}(x)] \right)^2 \right] + \sigma^2_{\varepsilon} $$

Что представляет собой

$$ Err(x) = Bias^2 + Variance + Noise $$

В случае дисперсии мы находим матожидание прогнозных значений различных моделей $E[\hat{f}(x)]$, вычитаем его из прогнозов моделей $\hat{f}(x)$, возводим в квадрат и находим матожидание отклонений.

Приведем разложение (здесь полезно вспомнить, что дисперсия равна матожиданию квадрата минус квадрат матожидания). Для простоты обозначим истинные значения как $y,$ прогнозные как $\hat{y}$.

$$ E(y-\hat{y})^2 = E(y^2 + \hat{y}^2-2y\hat{y}) = $$

$$ E(y^2)-(Ey)^2+(Ey)^2 + $$

$$ E(\hat{y}^2)-(E\hat{y})^2+(E\hat{y})^2-2(Ey\hat{y}) = $$

$$ Dy + D\hat{y} + (Ey)^2 +(E\hat{y})^2-2(Ey\hat{y}) = $$

$$ Dy + D\hat{y} + E(y-\hat{y})^2 $$

Как бороться с переобучением?

Сложная, переобученная модель может иметь очень много признаков (особенно если речь идёт о полиноме).

Очевидно, в большинстве случае визуальный подбор степени полинома (как мы это делали ранее для линейной и логистической полиномиальных регрессий) не представляется возможным. Более того, модели с таким количеством признаков в силу их высокой сложности (complexity) склонны к переобучению.

Бороться с этим можно тремя способами:

Первый вариант. Увеличить размер обучающей выборки. Маленькая выборка снижает обобщающую способность модели, а значит повышает разброс.

Второй вариант. Уменьшить количество признаков (вручную или через алгоритм, кроме того вводить наказание за новые признаки, как например, скорректированный коэффициент детерминации, adjusted R-square). Опасность здесь — выбросить нужные признаки.

Третий вариант. Использовать регуляризацию, которая позволяет снижать параметр (вес, коэффициент) признака и, таким образом, снижать его значимость. Предположим, что мы хотим уменьшить влияние второго признака в модели ниже.

$$ y = 15x_1 + 10x_2 + 5 \rightarrow y = 15x_1 + 5x_2 + 5 $$

Подобное изменение, как правило, приводит к тому, что модель меньше настраивается на шум (излишнюю вариативность) в обучающих данных и, как следствие, показывает лучшие результаты на тестовой выборке.

Другими словами, по сравнению с обычной линейной регрессией, у нее немного большее смещение (bias), но зато заметно меньший разброс (variance).

Три дополнительных соображения:

• Очевидно, что если мы снизим параметр признака до нуля, то этот признак будет удален из модели.
• Как правило, не имеет смысла применять регуляризацию к свободному коэффициенту $ \theta_0 $.
• Очень маленькие значения $\theta$ также могут повышать ошибку

Откроем ноутбук к этому занятию⧉

Регуляризация линейной регрессии

Рассмотрим несколько вариантов регуляризации линейной регрессии: Ridge, Lasso и Elastic Net.

Подготовка данных

Подгрузим данные о недвижимости в Бостоне, разделим на обучающую и тестовую части и выполним стандартизацию.

Ordinary Least Squares

Построим регрессию без регуляризации методом наименьших квадратов и выведем RMSE на обучающей и тестовой выборках.

Ridge Regression

Функция потерь

Ридж-регрессия (ridge regression, гребневая регрессия) вводит наказание (penalty) за слишком большие коэффициенты. Это наказание представляет собой сумму коэффициентов $ \theta $, возведенных в квадрат (чтобы положительные и отрицательные значения не взаимоудалялись).

$$ J_{Ridge}(\theta) = MSE + \sum{\theta_i^2} $$

Опять же $\theta_0$ здесь не учитывается. В векторизованной форме,

$$ J_{Ridge}(\theta) = MSE + \theta^T \theta $$

Корень из скалярного произведения вектора на самого себя есть его длина. Так как в данном случае мы корень не извлекаем, то можем записать слагаемое регуляризации (regularization term) как

$$ J_{Ridge}(\theta) = MSE + || \theta ||^2_2 $$

Наконец, введем еще одно дополнение, параметр $\lambda$, который позволит нам контролировать силу воздействия этого слагаемого на уровень ошибки.

$$ J_{Ridge}(\theta) = MSE + \alpha \cdot || \theta ||^2_2 $$

Замечу также, что Ridge Regression также называют L2-регуляризацией, потому что она использует L2-норму в качестве соответствующего слагаемого. Посмотрим на иллюстрацию регуляризации.

При регуляризации у нас появляется, по сути, две функции ошибки: основная (синяя), наказывающая за отклонение истинных значений от прогнозных. и дополнительная (оранжевая), наказывающая за отклонение коэффициентов от нуля. Их сумму и будет пытаться минимизировать алгоритм.

Источник картинки и подробности здесь⧉.

Нормальные уравнения

Вспомним аналитическое решение задачи линейной регрессии.

$$ \theta = (X^TX)^{-1}X^Ty $$

В случае нормальных уравнений с L2-регуляризацией оптимальное решение можно найти через

$$ \theta = (X^TX + \alpha I)^{-1}X^Ty $$

$I$ представляет собой единичную матрицу размером $ (j+1) \times (j+1) $ с нулевым значением первого столбца первой строки (сдвиг), где $j$ — количество признаков.

Что интересно, регуляризация решает проблему вырожденных или необратимых матриц. Матрица будет вырожденной в случае, если количество признаков больше количества объектов и может быть необратима, если оно равно количеству объектов. Выражение $X^TX + \alpha I $ решает эту проблему.

Напишем собственный класс.

Ошибка на обучающей выборке немного выросла, на тесте немного уменьшилась. Сравним с sklearn.

Выведем изменение коэффициентов на графике.

Метод градиентного спуска

Эту же задачу можно решить методом градиентного спуска. Функция потерь в этом случае будет иметь вид

$$ J({\theta_j}) = \frac{1}{2n} \sum (y-\theta X)^2 + \frac{1}{2n} \lambda \theta^T \theta $$

Для градиентного спуска, чтобы не запутаться, обозначим коэффициент скорости обучения через $\alpha$, а параметр регуляризации через $\lambda$. При этом градиент будет равен

$$ \frac{\partial}{\partial \theta_j} J(\theta) = \left( -x_j(y-X\theta) + \lambda \theta \right) \times \frac{1}{n} $$

Нормализовывать сдвиг не обязательно (в первую очередь имеют значения наклоны). Здесь мы это делаем, чтобы упростить код. Перейдем к практике. Начнем с собственного класса.

Сравним с sklearn. Для того чтобы оптимизировать Ridge регрессию методом градиентного спуска, используем класс SGDRegressor с параметром penalty = ‘l2’. Кроме того, укажем другие параметры для того, чтобы применяемый алгоритм был максимально близок к написанному вручную.

Выбор $\alpha$

Подобрать оптимальный гиперпараметр регуляризации можно, в частности, с помощью класса RidgeCV, который одновременно выполним оценку качества модели с помощью перекрестной валидации.

Темы перекрестной валидации и настройки гиперпараметров будут рассмотрены в курсе ML для продолжающих.

Приведем пример.

Lasso Regression

Регрессия Lasso для регуляризации использует сумму весов по модулю, то есть L1-норму.

Сравнение L1 и L2 регуляризации

$$ J_{Lasso}(\theta) = MSE + \alpha \cdot || \theta ||_1 $$

Отличие заключается в том, что Ridge-регрессия при возведении $\theta$ в квадрат сильнее «наказывает» за большие коэффициенты, Lasso «наказывает» все коэффициенты одинаково. Например, если $\theta$ равен $ \begin{bmatrix} 10 \\ 5 \end{bmatrix} $, то в первом случае L2-регрессии penalty составит $ 10^2 + 5^2 = 125 $, в случае L1, только 15. При увеличении первого коэффициента на единицу L2-penalty составит $ 11^2 + 5^2 = 146 $, L1 увеличится до 16.

Одновременно этот пример показывает особую важность масштабирования признаков при использовании алгоритма с регуляризацией.

Обнуление коэффициентов

L1 регуляризация может полностью обнулить часть коэффициентов и, таким образом, исключить соответствующие признаки из модели. Эта особенность Lasso регрессии называется parameter sparcity.

Математика

Вначале рассмотрим модель с L2-регуляризацией с одним признаком и одним коэффициентом $\theta$.

$$ L_2 = (y-x\theta)^2+\alpha\theta^2 = y^2-2xy\theta+x^2\theta^2+\alpha\theta^2 $$

Найдем производную относительно $\theta$, приравняем ее к нулю и решим для $\theta$.

$$ \frac{\partial L_2}{\partial \theta} = -2xy + 2x^2\theta + 2\alpha\theta $$

$$ -2xy + 2x^2\theta + 2\alpha\theta = 0 $$

$$ \theta(x^2 + \alpha ) = xy $$

$$ \theta = \frac{xy}{(x^2 + \alpha)} $$

Коэффициент $\theta$ превратится в ноль для ненулевых значений x и y при $\alpha \rightarrow \inf$. Сравним с L1-регуляризацией. Найдем производную относительно $\theta,$ приравняем к нулю и решим для $\theta$ для случаев $\theta > 0$ (в точке ноль производная функции не определена).

$$ \frac{\partial L_1}{\partial \theta} = -2xy + 2x^2\theta + \alpha $$

$$ -2xy + 2x^2\theta + \alpha = 0 $$

$$ 2x^2\theta = 2xy-\alpha $$

$$ \theta = \frac{2xy-\alpha}{2x^2} $$

Сдалаем то же самое для случая, когда $\theta < 0$.

$$ \frac{\partial L_1}{\partial \theta} = -2xy + 2x^2\theta-\alpha $$

$$ -2xy + 2x^2\theta-\alpha = 0 $$

$$ 2x^2\theta = (\alpha + 2xy) $$

$$ \theta = \frac{\alpha + 2xy}{2x^2} $$

В обоих случаях при определенных x, y и $\alpha$ параметр $\theta$ может быть равен нулю.

Дополнительно сравним L2 и L1 нормы двух векторов $ \begin{bmatrix} 1 \\ 0 \end{bmatrix} $ и $ \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} $.

В случае L2-нормы, их длина будет равна единице. В случае L1-нормы длина первого вектора будет равна единце, а второго $\sqrt{2} \approx 1,41$. Таким образом, L1 регуляризация не только допускает, но и способствует обнулению коэффициентов.

Визуализация

Приведем классическую визуализацию границ двух видов регуляризации из книги T. Hastie The Elements of Statistical Learning⧉ (страница 71).

Изолинии отображают уровни ошибки при определенных параметрах $\theta$. Синий ромб и круг задают соответственно границу L1 и L2 регуляризации.

Координатный спуск

Как уже было замечено, производная функции абсолютной величины не определена в точке $x = 0$ и, как следствие, мы не можем использовать обычный алгоритм градиентного спуска.

При этом мы можем двигаться вниз на каждой итерации лишь вдоль одной из координат и остановиться, если этот шаг окажется меньше, чем некоторое заданное нами пороговое значение. Такой метод называется методом координатного спуска (coordinate descent).

Приведем иллюстрацию из Википедии⧉.

Выбрать, по какой координате спускаться можно разными способами, в частности, можно:

• выбирать признак (координату) случайным образом или
• просто идти от признака 0 до j (далее признаки мы будем обозначать так)

Рассмотрим как координатный спуск выглядит с точки зрения математики.

Математика

Итак, напомню, функция потерь будет иметь вид

$$ J_{Lasso}(\theta) = MSE + \alpha \cdot || \theta ||_1 $$

Вначале обратимся к первому компоненту, а именно MSE. Вспомним, чему равен градиент MSE.

$$ \frac{\partial J}{\partial \theta_j} = \frac{1}{n} \times -x_j(y-X\theta) $$

Перепишем $y-X\theta$ как $y-(\theta_kX_k+\theta_jx_j)$.

$$ \frac{1}{n} \times -x_j(y-(\theta_kX_k+\theta_jx_j)) $$

Другими словами, выделим ту координату j (признак), по которой мы будем спускаться в этот раз. $\theta_kX_k$ — это прогноз модели без коордианты j. Раскроем, а затем реорганизуем скобки.

$$ \frac{1}{n} \times -x_j((y-\theta_kX_k)-\theta_jx_j)$$

Умножим $-x_j$ на каждое из слагаемых.

$$ \frac{1}{n} \times -x_j((y-\theta_kX_k) + \theta_j x_j^2 $$

Обозначим компоненты через новые переменные $\rho$ («ро») и $z$.

$$ \rho_j = x_j((y-\theta_kX_k) $$

Примечание. Минус перед $x_j$ появится в окончательной формуле ниже.

$$ z_j = x_j^2 $$

Переменная $\rho$ по сути показывает насколько признак $x_j$ коррелирует с остатками модели $y-\theta_kX_k$, построенной без j. Если $\rho$ (т.е. корреляция) растет, значит этот признак важен для модели и его вес стоит увеличить.

Тогда выражение будет иметь вид

$$ \frac{\partial L}{\partial \theta_j} = -\frac{1}{n}\rho_j + \frac{1}{n} \theta_jz_j $$

Приравняв производную к нулю, найдем решение относительно $\theta_j$.

$$ \theta_j = \frac{\rho_j}{z_j} $$

Замечу, что $z_j$, то есть скалярное произведение вектора признака $x_j$ самого на себя, будет равно единице, если признаки будут предварительно нормализованы (приведены к единичной L2 норме).

Обратимся ко второму компоненту, слагаемому регуляризации. Так как производная в точке $|\theta_j| = 0$ не определена, воспользуемся таким понятием как субградиент (subgradient). По сути, субградиентом является множество возможных градиентов в определенной точке. Приведем иллюстрацию для субградиентов в точке $|\theta_j| = 0$.

Как видно, субградиенты могут принимать значения $[-1, 1]$ (градиенты функции абсолютного значения) или вернее от $[-\alpha, \alpha]$, то есть параметра, на который мы умножаем слагаемое регуляризации.

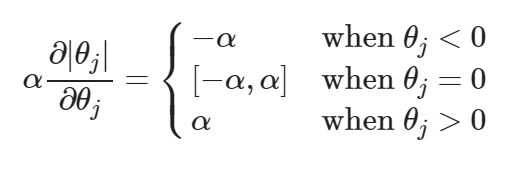
Объединим две производных.

Рассмотрим каждый из трех случаев по отдельности.

Вариант 1. $\theta_j < 0$

$$ -\frac{1}{n}\rho_j + \frac{1}{n} \theta_jz_j-\alpha = 0 $$

$$ \theta_j = \frac{\rho_j + n\alpha}{z_j} $$

Для того чтобы $\theta_j < 0$, необходимо чтобы $\rho_j < n\alpha $

Вариант 2. $\theta_j = 0$

$$ -\frac{1}{n}\rho_j + \frac{1}{n} \theta_jz_j + [-\alpha, \alpha] = 0 $$

$$ \theta_j = \left[ \frac{\rho_j-n\alpha}{z_j}, \frac{\rho_j + n\alpha}{z_j} \right] $$

Для того чтобы $ \theta_j = 0 $, $ -n\alpha\ \leq \rho_j \leq n\alpha $.

Вариант 3. $\theta_j > 0$

$$ -\frac{1}{n}\rho_j + \frac{1}{n} \theta_jz_j + \alpha = 0 $$

$$ \theta_j = \frac{\rho_j-n\alpha}{z_j} $$

Для того чтобы $\theta_j > 0$, $\rho_j > n\alpha $

Сдвиг $\theta_0$ не регуляризуется и изменяется с помощью частной производной MSE (первое слагаемое).

$$ \theta_0 = \frac{\rho_0}{z_0} $$

Таким образом, шаги алгоритма координатного спуска будут следующими:

Шаг 1. Добавить первый (!) столбец из единиц для коэффициента $\theta_0$. Инициализировать веса $\theta$.

Шаг 2. Рассчитать $z_j$.

$$ z_j = \sum x_j^2 $$

Шаг 3. Задать начальный максимальный размер шага (max_step) и пороговое значение (tolerance)

Шаг 4. Пока максимальный размер шага больше порогового значения проходиться в цикле по каждой из координат (признаку), рассчитать $ \rho_j = \sum x_j((y-\theta_kX_k) $ и обновлять вес $\theta$ этого признака в соответствии со следующими правилами:

Если j = 0, то есть первого по счету коэффициента $\theta_0$, то $\theta_j = \frac{ρ_j}{z_j}$.

В остальных случаях

$$ \theta_j = \left\{ \begin{matrix} \frac{\rho_j + n \alpha}{z_j} & if & \rho_j < -n \alpha \\ 0 & if & -n \alpha ≤ \rho_j ≤ n \alpha \\ \frac{\rho_j-n \alpha}{z_j} & if & \rho_j > n \alpha \end{matrix} \right. $$

Обратите внимание, если $ -n\alpha\ \leq \rho_j \leq n\alpha $ (то есть корреляция признака очень мала по модулю), то коэффициент будет обнулен и исключен из модели. В двух других случаях (варианты 1 и 3), мы будем увеличивать коэффициент при большом отрицательном $\rho_j$ и уменьшать при большом положительном (т.е. выполнять регуляризацию). Посмотрим на график ниже.

Такое ограничение называется мягким порогом (soft thresholding). Приведем для сравнения Ridge регрессию, которая сокращает коэффициенты на всем диапазоне $\theta$, но не приводит их к нулевым значениям.

Реализация на Питоне

Объявим вспомогательные функции.

Объявим функцию координатного спуска.

Протестируем алгоритм.

Мы видим, что модель сочла признак INDUS не имеющим значения для данной модели и обнулила соответствующий коэффициент. Сравним с классом Lasso библиотеки sklearn.

Elastic Net Regression

Регрессия Elastic Net использует как L1, так и L2 регуляризацию.

$$ J_{ElasticNet}(\theta) = MSE + \alpha_1 \cdot || \theta ||_1 + \alpha_2 \cdot || \theta ||_2^2 $$

Так как в этой модели есть компонент L-1, для которого в точке $|\theta_j| = 0$ производная не определена, используем один из возможных субградиентов, а именно нулевой субградиент (красная пунктирная линия $g_3$ на рисунке выше).

Другими словами, субградиент для компонента будет выглядеть следующим образом

$$ \frac{\partial J_{L1}}{\partial_{sub} \theta} = \left\{ \begin{matrix} 1 & if & \theta > 0 \\ 0 & if & \theta = 0 \\ -1 & if & \theta < 0 \end{matrix} \right. ​$$

Это условие соответствует сигнум-функции или функции знака (sign function⧉). На Питоне можно использовать np.sign().

Сравним с классом ElasticNet библиотеки sklearn.

Замечу, что класс ElasticNet библиотеки sklearn использует координатный спуск для минимизации функции потерь. Кроме того, в документации можно посмотреть, как единственный параметр $\alpha$ регулирует значимость L1 и L2 компонентов.

Регуляризация нейросети

В качестве иллюстрации приведем примеры L2 регуляризации нейронной сети.

Функция потерь с регуляризацией

Посмотрим на функцию потерь с учетом регуляризации (бинарная классификация)

$$ J_{reg}(W) = -\frac{1}{n} \sum y \cdot log(a^{(L)}) + (1-y) \cdot log(1-a^{(L)}) + $$

$$ + \frac{\alpha}{2n} \sum_l \sum_k \sum_j W^{(l)}_{k,j} $$

Уточним нотацию, мы находим уровень ошибки на основе значений выходного слоя $a^{(L)}$. Кроме того, мы добавляем значение регуляризации, которое рассчитывается как сумма $\sum_l$ сумм весов слоев $k$ и $j$ ($\sum_k$ и $\sum_j$). Приведем код.

Реализуем модель с регуляризацией на Питоне на основе уже созданного алгоритма бинарной классификации со смещением с двумя признаками и одним скрытым слоем (три нейрона) и сравним результаты обучения.

Подготовка данных

Обучение модели

Обучим модель.

Сделаем прогноз.

Выведем веса.

По сравнению с моделью без регуляризаци, точность на обучающей выборке, а также веса модели снизились.

Регуляризация в библиотеке Keras

Приведем регуляризацию модели в библиотеки Keras.

В целом регуляризаторы в Keras можно задавать следующим образом.

Подведем итог

На сегодняшнем занятии мы изучили концепции смещения и разброса модели, рассмотрели принцип L1 и L2 регуляризации и протестировали регуляризацию на линейной регрессии и нейросети. Также мы познакомились с алгоритмами координатного и субградиентного спуска.

В заключение, приведем советы Эндрю Ына по тому, что делать, если модель не показывает нужные результаты (то есть имеет высокое смещение или разброс):

• увеличить обучающую выборку
• уменьшить количество признаков
• найти или создать новые признаки
• использовать полиномиальные признаки или увеличить количество слоев/нейронов в нейросети
• уменьшить или увеличить параметр регуляризации $ \alpha $

Дополнительные материалы

Бэггинг для снижения разброса

Нам не обязательно использовать прогноз только одной модели. Можно взять группу или ансамбль (от франц. ensemble — «вместе») моделей.

На курсе «ML для продолжающих» мы поговорим про техники ансамблирования (ensemble methods) или объединения алгоритмов.

Сейчас же давайте рассмотрим один из этих способов, а именно бэггинг (bagging) и постараемся с его помощью снизить разброс модели.

Про бэггинг

Бэггинг (bagging) или bootstrap aggregating предполагает три основных шага:

1. Bootstrapping. За счет случайных выборок с возвращением (random samples with replacement) создается несколько датасетов на основе исходных данных (subsets). Это означает, что в каждом датасете могут быть как повторяющиеся объекты, так и объекты из других датасетов.
2. Parallel training. Затем модели (их называют базовыми моделями, base estimators, или weak learners) обучаются параллельно и независимо друг от друга.
3. Aggregation. Наконец, в зависимости от типа задачи, т.е. регрессии или классификации, рассчитывается, соответственно, среднее значение (soft voting) или класс, предсказанный большинством (hard/majority voting).

Алгоритм решающего дерева

Рассмотрение решающих деревьев (decision trees), алгоритма, который мы будем использовать внутри бэггинга, выходит за рамки сегодняшнего занятия. Мы начали знакомиться с этой темой на занятии работе с выбросами и более детально изучим на последующих курсах.

При этом будет важно сказать, что одним из недостатков этого алгоритма (когда используется только одно дерево) как раз является склонность к переобучению и высокий разброс модели. Посмотрим, сможет ли бэггинг исправить ситуацию.

Подготовка данных

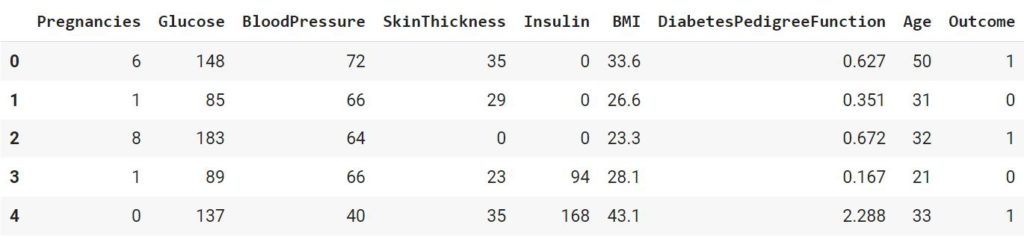
Используем данные о пациентах с диабетом.

Полезные ссылки

Bias-variance decomposition⧉

Ансамбли в машинном обучении⧉

Перейдем к теме градиентного спуска.