Выбросы в данных

Все курсы > Анализ и обработка данных > Занятие 9

Отдельным вопросом работы с количественными данными являются выбросы (outliers), которые существенно влияют на многие статистические показатели, мешают масштабировать данные и ухудшают качество моделей машинного обучения.

Откроем ноутбук к этому занятию⧉

Для визуализации некоторых результатов потребуется обновить sklearn и перезапустить среду выполнения.

Про выбросы

Понятие и причины выбросов

Выбросы — это данные, которые сильно отличаются от общего распределения. При этом можно выделить:

• ошибочно возникающие выбросы
  • человеческий фактор, ошибка ввода данных
  • погрешности измерения
  • ошибка эксперимента (например, шум при записи голоса)
  • ошибка обработки
  • ошибки получения выборки (sampling error)
• естественные выбросы
  • высокий человек, разовая большая покупка
  • аномально низкая цена на отдельный объект недвижимости

Примечание. В последнем случае, хотя с точки зрения модели такой выброс будет считаться нежелательным, имеет смысл проверить, с чем связана такая цена.

Влияние выбросов

Статистические показатели. На занятии по статистическому выводу мы провели тест Стьюдента, для того, чтобы определить на основе выборки вероятность того, что средний рост составляет 182 см.

Напомню, что исходя из данных мы смогли отвергнуть нулевую гипотезу, которая утверждала, что рост дейсвительно составляет 182 см.

Добавим выброс и повторно проверим гипотезу.

Как мы видим, одно сильно отличающееся наблюдение изменило результаты теста.

Масштабирование данных. Как мы только что видели, сильно отличающиеся от остальных значения мешают качественному масштабированию данных.

Модели ML. Выбросы влияют на качество модели линейной регрессии. Возьмем третий набор данных из квартета Энскомба (Anscombe’s quartet).

Посмотрим на коэффициент корреляции.

Удалим выброс.

Вновь посмотрим на график и коэффициент корреляции.

Выбросы особенно сильны, когда мы располагаем небольшим количеством данных.

Outlier vs. Novelty

Отличающееся наблюдение можно разделить на выбросы (outlier) и новые отличающиеся наблюдения (novelty). Выброс уже присутствует в данных. То есть мы смотрим на данные и понимаем, что часть содержащихся в них наблюдений существенно отличаются от общей массы. Во втором случае, у нас уже есть набор данных, нас просят определить, является ли новое наблюдение выбросом или нет.

Так как для выявления уже присутствующих выбросов у нас нет никакой разметки, это обучение без учителя. Во втором случае, это частичное обучение с учителем (semi-supervised). На практике это означает, что при использовании продвинутых алгоритмов для выявления выбросов, если речь идет о новых отличающихся наблюдениях (novelty), мы должны использовать .fit() на обучающей выборке, а .predict(), .decision_function() и .score_samples() на тестовой (про алгоритмы и эти методы поговорим дальше). Подробнее здесь⧉.

Работа с выбросами

Начнем с более простых методов. Скачаем и подгрузим данные.

Статистические методы

boxplot

Выбросы можно увидеть на boxplot. По умолчанию, длина «усов» рассчитывается как $ 1,5 \times IQR $. Данные, которые выходят за их пределы — выбросы.

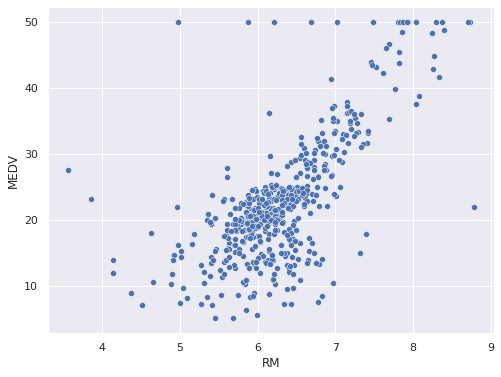
scatter plot

Кроме того, выбросы можно попытаться выявить на точечной диаграмме.

z-score

Количественно выбросы можно найти через стандартизированную оценку (z-оценку, z-score). Эта оценка показывает на сколько средних квадратических отклонений значение отличается от среднего.

Так как мы знаем, что 99,7 процентов наблюдений лежат в пределах трех СКО от среднего, то можем предположить, что выбросами будут оставшиеся 0,3 процента.

Выведем эти значения.

Посмотрим, как удалить выбросы в отдельном столбце.

Теперь удалим выбросы во всем датафрейме.

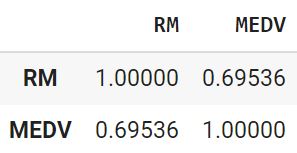
Выведем корреляцию до и после удаления выбросов.

В данном случае корреляция увеличилась.

Измененный z-score

Важно понимать, что z-score, который мы используем для идентификации выбросов сам по себе зависит от сильно отличающихся значений, поскольку для расчета используется среднее арифметическое и СКО.

$$ z = \frac {x-\mu}{\sigma} $$

Вместо z-оценки можно использовать изменнную z-оценку (modified z-score), которая использует метрики робастной статистики.

$$ z_{mod} = \frac{x-Q2}{MAD} $$

где MAD представляет собой среднее абсолютное отклонение (median absolute deviation) и рассчитывается по формуле $MAD = median(|x-Q2|). Заметим⧉, что $MAD=0,6745\sigma$.

Iglewicz и Hoaglin рекомендуют считать выбросами те значения, для которых $|z_{mod} > 3,5|$. Применим этот метод.

Обратите внимание, что в данном случае мы очень агрессивно удаляли значения. Посмотрим на корреляцию.

1.5 IQR

Еще одним распространенным способом выявления и удаления выбросов является правило $ 1,5 \times IQR $. Рассмотрим, почему именно 1,5? В стандартном нормальном распределении Q1 и Q3 соответствуют $-0.6745\sigma$ и $0.6745\sigma$.

Зная эти показатели, мы можем рассчитать верхнюю и нижнюю границу.

Замечу, что для того, чтобы этот метод нахождения выбросов был аналогичен z-score, было бы точнее использовать показатель $ 1,75 \times IQR $. При таком решении выбросами будет считаться большее количество наблюдений.

Найдем и удалим выбросы в столбце.

Найдем и удалим выбросы во всем датафрейме.

Как мы видим, несмотря на более активное удаление значений, коэффициент корреляции стал даже меньше, чем в изначальных данных.

Методы, основанные на модели

Теперь посмотрим на методы выявления выбросов, основанные на модели (model-based approaches)

Isolation Forest

Изолирующий лес (Isolation Forest или iForest) использует принципы решающего дерева (Decision Tree) и построенного на его основе ансамблевого метода случайного леса (Random Forest).

Принцип изолирующего леса

Принцип построения изолирующиего дерева (Isolation Tree или iTree) довольно прост. Алгоритм случайным образом выбирает признак, затем в пределах диапазона этого признака случайно выбирает разделяющую границу (split). Та часть наблюдений, которая меньше либо равна этой границые. оказывается в левом потомке (left child node), та которая больше — в правом (right child node). Затем процесс рекурсивно повторяется.

Что интересно, в получившейся древовидной структуре путь (то есть количество сплитов) от корневого узла (root node) до выброса будет существенно короче, чем до обычного наблюдения. Это логично, например, в задаче классификации с помощью решающего дерева в первую очередь удается отделить тот класс, который наиболее удален от остальных.

Приведем классификацию с помощью решающего дерева на примере датасета цветов ириса.

Как вы видите, нулевой, наиболее удаленный класс (синие точки) удалось отделить уже на первом шаге. По этому же принципу отделяются выбросы.

Лес изолирующих деревьев соответственно дает усредненное расстояние до каждой из точек.

Показатель аномальности

Рассмотрим как количественно выразить среднее расстояние до каждой из точек или показатель аномальности (anomaly score). Приведем формулу.

$$ s(x, n) = 2^{-\frac{E(h(x))}{c(n)}} $$

где x — это конкретное наблюдение из общего числа n наблюдений. При этом c(n) — это средний путь до листа в аналогичном по структуре двоичном дереве поиска (binary search tree, BST) с n наблюдений, а $ E(h(x)) $ — усредненное по всем деревьям расстояние до конкретного наблюдения x. Нормализуя показатель $ E(h(x)) $ по c(n) мы получаем, что:

• когда $ E(h(x)) \rightarrow c(n), s \rightarrow 0,5 $
• когда $ E(h(x)) \rightarrow 0, s \rightarrow 1 $
• когда $ E(h(x)) \rightarrow n-1, s \rightarrow 0 $

При этом расстояние $h(x)$ находится в диапазоне $(0, n-1]$, а s в диапазоне $(0, 1]$. Таким образом,

• если наблюдение имеет s, близкое к 1, это выброс
• если наблюдение имеет s, близкое к 0, это не выброс
• если s всех наблюдений близко к 0,5, тогда вся выборка не имеет выбросов

Более подробно про этот алгоритм можно прочитать в публикации его создателей Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. “Isolation forest.” Data Mining, 2008. ICDM’08. Eighth IEEE International Conference⧉.

IsolationForest в sklearn

Пример из sklearn

Разберем пример⧉, приведенный на сайте sklearn. Вначале создадим синтетические данные с выбросами.

Разделим выборку.

Обучим класс изолирующего леса. Так как наблюдений мало, для каждого дерева будем брать все объекты обучающей выборки.

Сделаем прогноз на тесте и посмотрим на результат.

Выведем решающую границу.

Настройка гиперпараметров

Разберем гиперпараметры модели:

• n_estimators — количество деревьев в изолирующем лесу
• max_samples — количество наблюдений для обучения каждого изолирующего дерева
• max_features — количество признаков для обучения каждого дерева
• bootstrap — получение выборки (sampling) с возвращением (True) или без (False).
• contamination — доля выбросов в датасете
  • значение auto определяет выбросы так, как это было описано в публикации авторов, но с измененным порогом: anomaly score выброса отрицателен и близок к $-1$, anomaly_score обычного наблюдения положителен и близок к 0
  • кроме того, можно задать конкретную ожидаемую долю выбросов, например, 0,1 сделает выбросами 10 процентов наблюдений с самым высоким anomaly score

Продемонстрируем особенности параметра contamination на простом примере. Возьмем небольшой набор данных и поочередно применим параметры contamination = ‘auto’, 0.1, 0.2. Несколько пояснений:

• метод .predict() помечает обычные наблюдения значением 1, выбросы значением $-1$
• метод .decision_function() выдает anomaly_score

Датасет boston

Применим алгоритм изолирующего леса к датасету boston.

Посмотрим на взаимосвязь признака RM с целевой переменной после удаления выбросов.

Недостаток алгоритма

Для того чтобы увидеть недостаток алгоритма, рассмотрим тепловую карту, на которой цветом будут выводиться области с одинаковым anomaly score.

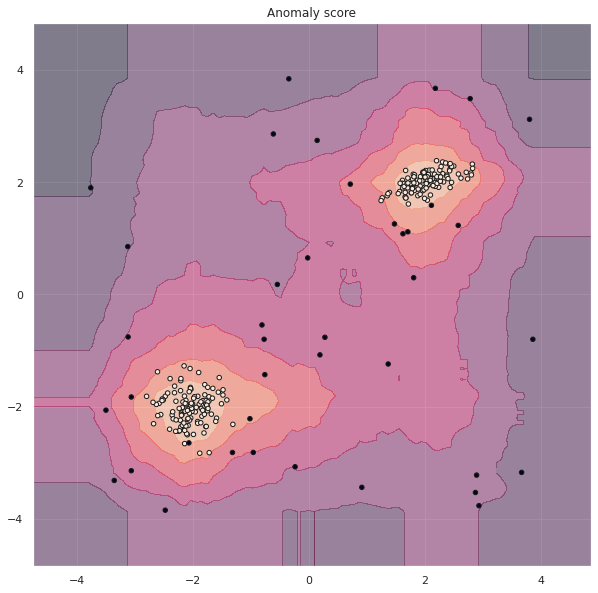
Как вы видите, в верхнем левом и нижнем правом углу также находятся области (их называют ghost areas), в которых объекты могли бы быть классифицированы как обычные наблюдения, хотя это неправильно (ложноположительный результат). Это связано с тем, что границы, проводимые алгоритмом параллельны осям координат.

Приведем иллюстрацию из статьи⧉ исследователей, усовершенствовавших этот алгоритм.

Для решения этой проблемы был предложен расширенный алгоритм изолирующего леса.

Extended Isolation Forest

Расширенный алгоритм изолирующего леса (Extended Isolation Forest) делит пространство с помощью случайных, не обязательно параллельных осям координат, гиперплоскостей. Авторами этого алгоритма являются Sahand Hariri, Matias Carrasco Kind и Rober J. Brunner⧉. Для данных на предыдущей иллюстрации разделение с помощью расширенного алгоритма могло бы выглядеть вот так.

Рассмотрим работу этого алгоритма на практике. Приведу две библиотеки, в которых реализован Extended Isolation Forest.

• Библиотека eif⧉, созданная авторами алгоритма; и
• Extended Isolation Forest на платфоме h2o⧉.

Используем второй вариант.

Платформа h2o

Установим h2o в Google Colab.

Запустим сервер h2o.

Обучение алгоритмов

Импортируем класс алгоритма⧉, создадим объекты этого класса для модели обычного изолирующего леса (без наклона гиперплоскостей) и для модели с максимальным наклоном гиперплоскостей.

Максимальный наклон задается параметром extension_level и находится в диапазоне $[0, P-1]$, где P — это количество признаков. В нашем случае признаков два, поэтому для расширенного алгоритма используем extension_level = 1.

Сравнение алгоритмов

Так как Extended Isolation Forest — это алгоритм без учителя (метод .predict() выдает anomaly_score), мы не можем напрямую посчитать точность прогноза. С другой стороны, так как в созданных нами данных есть разметка, мы можем провести косвенное сравнение.

Например, мы можем отсортировать данные по anomaly_score в убывающем порядке (то есть в начале будут наблюдения, которые наиболее вероятно являются выбросами) и посмотреть, какое количество единиц (то есть не выбросов), оказалось в результатах сортировки каждого из алгоритмов.

Начнем с алгоритма обычного изолирующего леса. Сделаем прогноз.

Создадим датафрейм из исходных признаков и целевой переменной.

Определимся с долей наблюдений, в которых будем считать количество выбросов и не выбросов.

Соединим датафрейм с признаками и целевой переменной с показателями аномальности. Затем отсортируем по этой метрике в убывающем порядке и рассчитаем количество выбросов и не выбросов в имеющихся данных.

Итак, в 60-ти наблюдениях с наибольшим anomaly score обычный алгоритм поместил 39 выбросов и 21 не выброс.

Сделаем то же самое с расширенным алгоритмом.

Расширенный алгоритм сделал чуть менее качественный прогноз.

Визуализация

Сравним тепловые карты обоих алгоритмов.

В данном случае, как мы видим, расширенному алгоритму не удалось сформировать два обособленных кластера.

Подведем итог

На сегодняшнем занятии мы разобрали статистические методы выявления выбросов (boxplot, scatter plot, z-score и 1,5 IQR), а также два метода, основанные на модели (алгоритмы обычного и расширенного изолирующего леса).

Перейдем к теме кодирования категориальных переменных.