Кластерный анализ | Вводный курс ML

Все курсы > Вводный курс > Занятие 16

Основная идея кластерного анализа (clustering, cluster analysis) заключается в том, чтобы разбить объекты на группы или кластеры таким образом, чтобы внутри группы эти наблюдения были более похожи друг на друга, чем на объекты другого кластера.

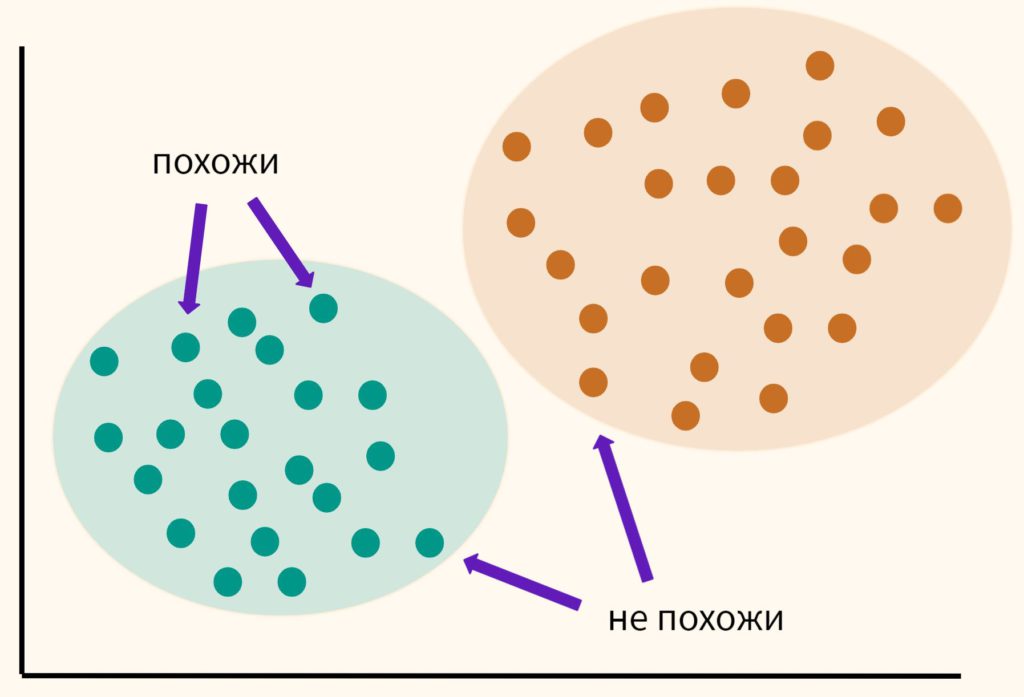
При этом мы заранее не знаем на какие кластеры необходимо разбить наши данные. Это связано с тем, что мы обучаем модель на неразмеченных данных (unlabeled data), то есть без целевой переменной, компонента y. Именно поэтому в данном случае говорят по машинное обучение без учителя (Unsupervised Learning).

Кластерный анализ может применяться для сегментации потребителей, обнаружения аномальных наблюдений (например, при выявлении мошенничества) и в целом для структурирования данных, о содержании которых мало что известно заранее.

Содержание занятия

Как же разбить данные на кластеры?

Изучая векторы и матрицы, мы узнали, что векторы данных можно сравнивать между собой (оценивать их схожесть), измеряя расстояние между ними. Кластерный анализ использует именно этот подход. Мы измеряем расстояние между точками и на основе этого измерения принимаем решение к какому кластеру отнести то или иное наблюдение.

В рамках этого занятия мы поговорим про алгоритм, который называется методом k-средних (k-means clustering method).

Метод k-средних

Давайте пошагово разберемся в том, как работает этот алгоритм.

Шаг 1. Вначале возьмем данные и самостоятельно выберем желаемое количество кластеров и обозначим их буквой k (отсюда название метода). Пусть в данном случае их будет три.

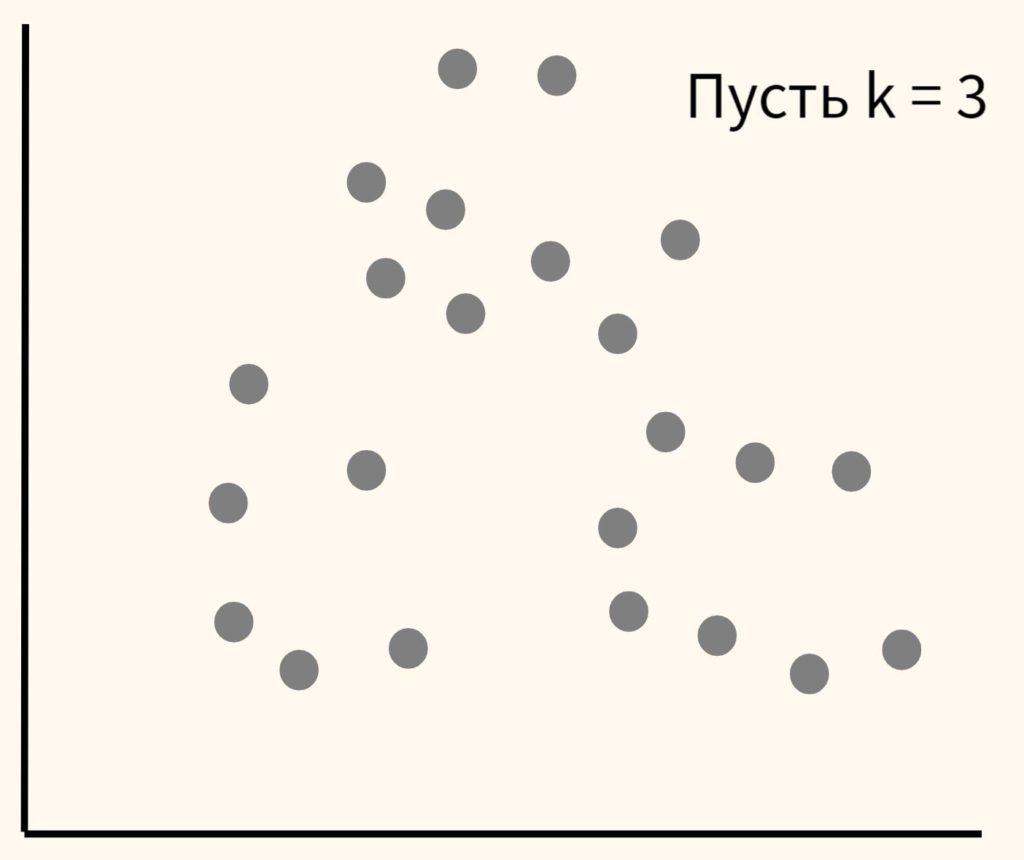
метод к-средних, шаг 1, выбор количества кластеров

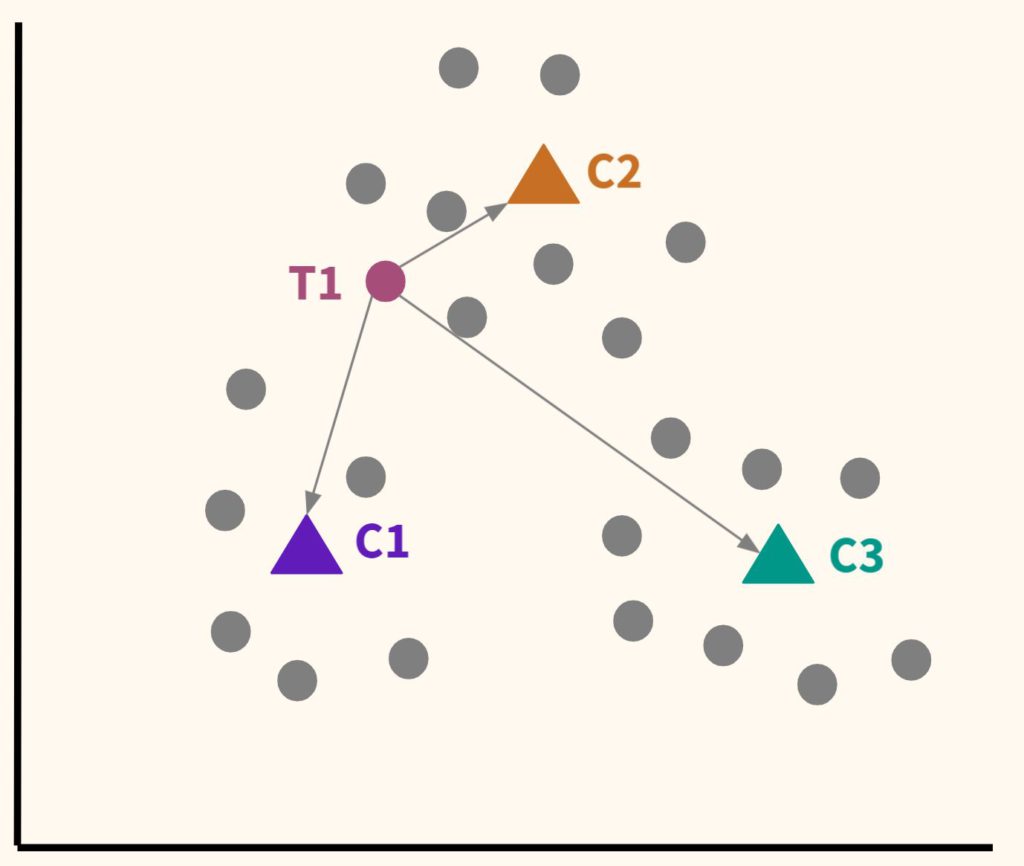
Шаг 2. Расположим несколько точек. Их количество будет равно количеству кластеров. Эти точки называются центроидами. Посчитаем расстояние от наших данных до каждого из центроидов. Логично отнести наблюдение к тому центроиду, который находится ближе.

метод к-средних, шаг 2, выбор центроидов

В частности, T1 будет отнесена к C2.

Шаг 3. Таким образом, каждая точка будет отнесена к определенному центроиду (кластеру).

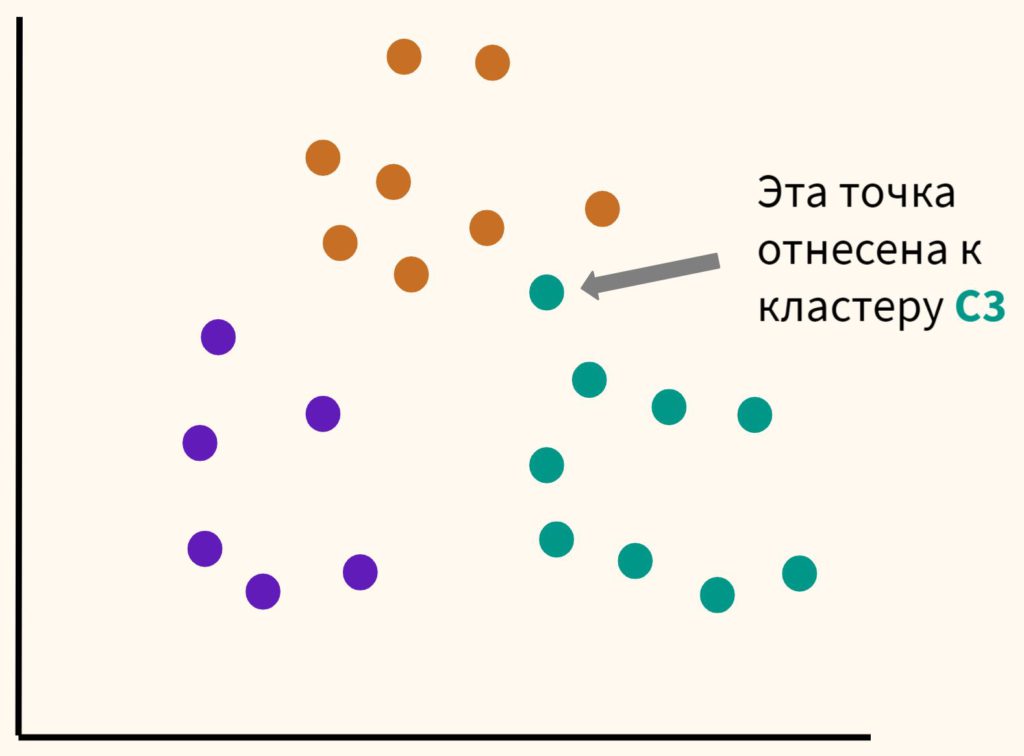
метод к-средних, шаг 3, распределение точек между центроидами

Шаг 4. Сместим наши центроиды в центр получившихся кластеров.

метод к-средних, шаг 4, смещение центроидов в центр получившихся кластеров

Шаг 5. Вновь отнесем точки к каждому из центроидов. Некоторые наблюдения «переметнутся» к другому центроиду.

метод к-средних, шаг 5, повторное распределение точек между центроидами

Мы будем повторять шаги 4 и 5 до тех пор, пока алгоритм не стабилизируется, то есть до тех пор, пока наблюдения не перестанут переходить от одного центроида (кластера) к другому.

Говоря более формально, цель алгоритма — минимизировать сумму квадратов внутрикластерных расстояний до центра кластера (within-cluster sum of squares, WCSS, наша функция потерь):

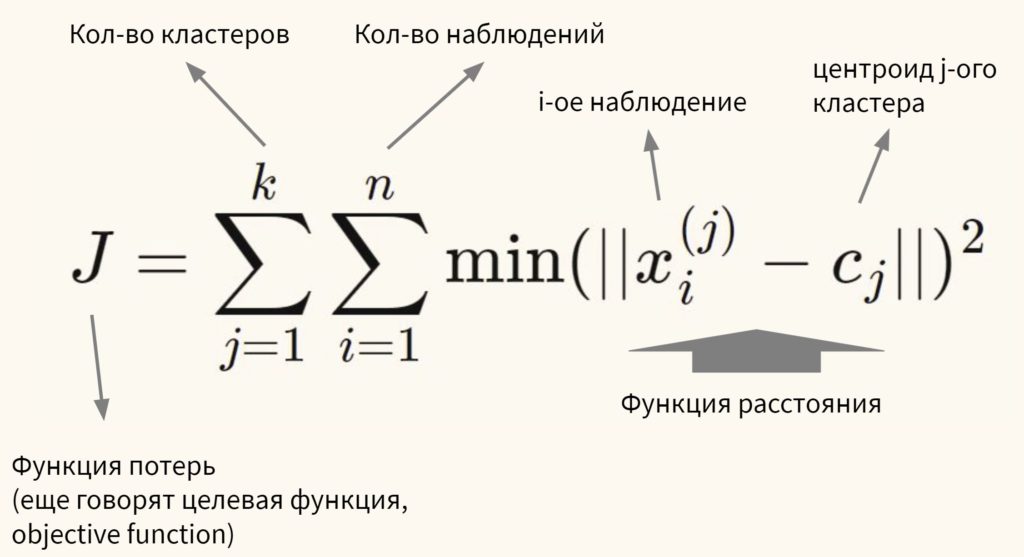
формула суммы квадратов внутрикластерных расстояний (WCSS)

Остается нерешенным важный вопрос.

Сколько кластеров выбрать?

Есть два способа выбора количества кластеров:

Экспертный метод. Выбор количества кластеров будет зависеть от знания о предметной области (domain knowledge)
Метод локтя (elbow method). Мы также можем (1) обучить модель используя несколько вариантов количества кластеров, (2) измерить сумму квадратов внутрикластерных расстояний и (3) выбрать тот вариант, при котором данное расстояние перестанет существенно уменьшаться.

На графике метод локтя выглядит следующим образом.

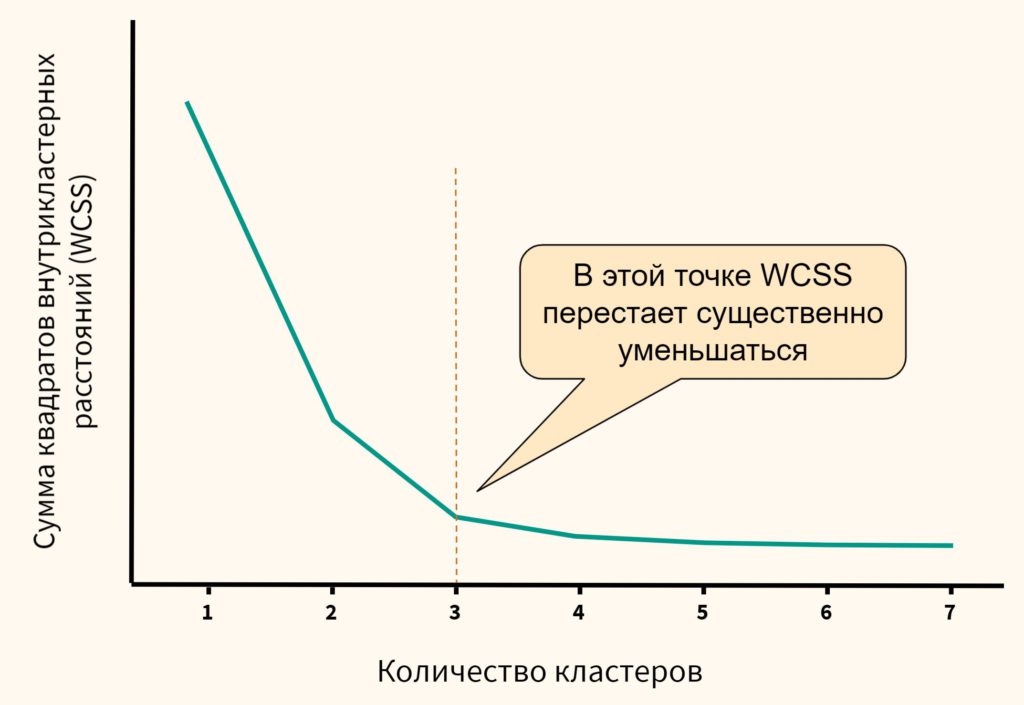
метод локтя для минимизации суммы квадратов внутрикластерных расстояний (WCSS)

Как мы видим, после того как количество кластеров достигает трех, сумма квадратов внутрикластерных расстояний перестает существенно уменьшаться. Значит в данном случае три кластера и будет оптимальным значением.

О важности нормализации данных

Алгоритм очень чувствителен к масштабу признаков. В связи с этим нормализация данных (feature scaling) приобретает особое значение. Так как при формировании кластеров мы измеряем расстояние (в частности, Евклидово расстояние), то признаки с большим масштабом будут иметь больший вес. Приведу пример.

Предположим у вас есть данные о возрасте и ежемесячных тратах людей по кредитным картам.

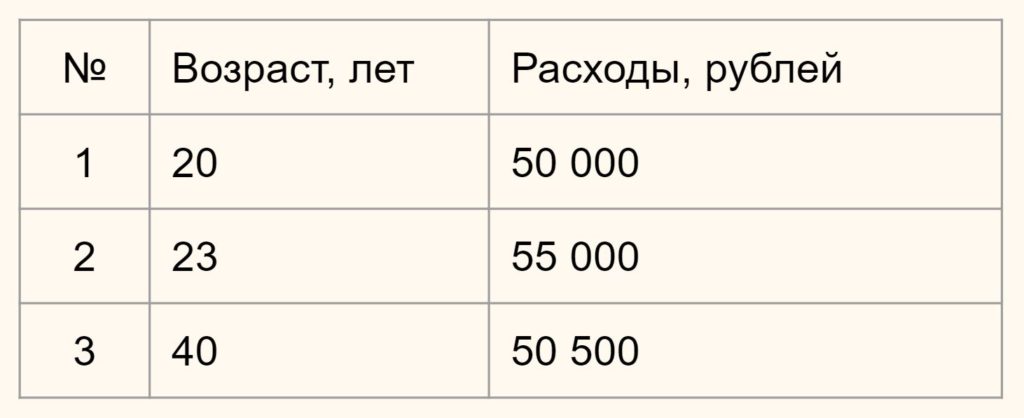
Нам нужно определить насколько человек 1 отличается (насколько велико расстояние) от человека 2 и 3. В зависимости от этого мы будем формировать наши кластеры.

Вначале давайте обратимся к здравому смыслу. Мы видим, что респонденты 1 и 2 схожи, потому что им обоим около 20-ти и расходы у них примерно одинаковы. Респондент 3, имея схожие расходы, сильно отличается из-за своего возраста. Он в два раза старше. Это особенно легко увидеть на графике ниже:

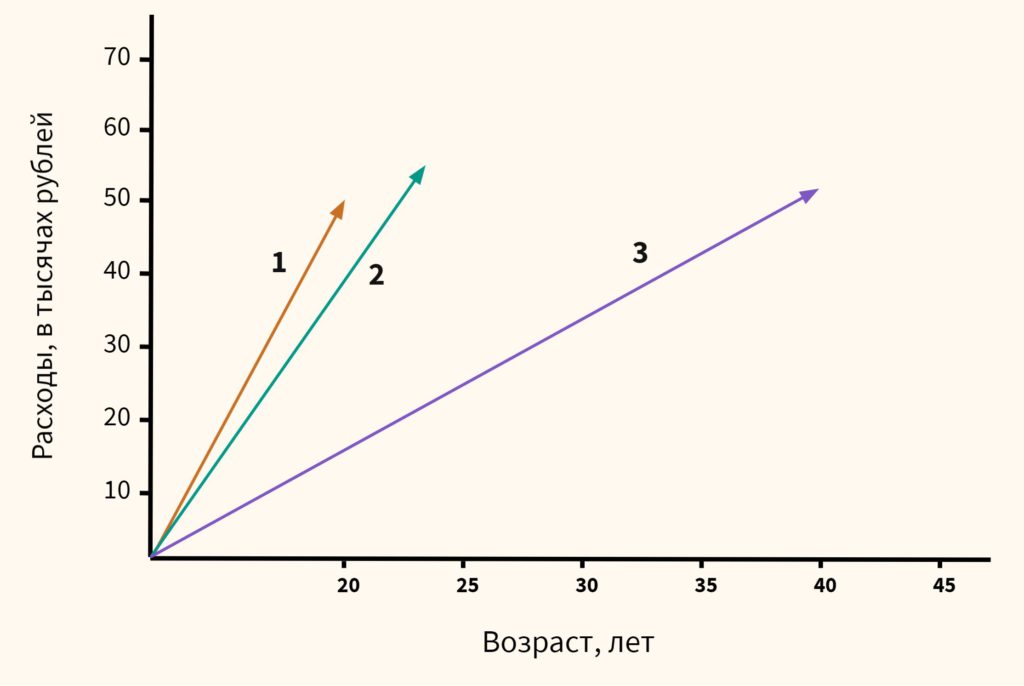
Теперь посмотрим, что скажет математика, если мы оставим масштаб признаков без изменений.

Евклидово расстояние

Ранее мы рассмотрели возможность измерения близости двух векторов с помощью косинусного сходства. Еще одним способом измерения близости векторов является так называемое евклидово расстояние (Eucledean distance).

Приведем сравнительную иллюстрацию.

косинусное сходство и евклидово расстояние

Косинусное сходство предполагает нахождение угла $\theta$ между векторами, а в случае евклидового расстояния мы вычисляем длину вектора $D$, соединяющего концы исходных векторов.

Для двумерных векторов евклидово расстояние рассчитывается по следующей формуле

$$ D = \sqrt {\left( {x_1-x_2 } \right)^2 + \left( {y_1-y_2 } \right)^2} $$

В примере выше x₁ и x₂ — это возраст двух сравниваемых нами людей, а y₁ и y₂ — их расходы. Подставим значения в формулу.

$$ D_1 = \sqrt {\left( {23-20 } \right)^2 + \left( {55000-50000 } \right)^2 } \approx 5000 $$

$$ D_2 = \sqrt {\left( {40-20 } \right)^2 + \left( {50500-50000 } \right)^2 } \approx 500 $$

Как мы видим, расстояние от человека 1 до человека 2 целых 5000 единиц (лет и рублей), в то время как до человека 3 только 500. Результат обратный тому, на который мы рассчитывали исходя из здравого смысла.

Это связано с тем, что масштаб второго признака (расходов) намного больше масштаба первого (возраст). И даже небольшое изменение в расходах вызывает существенное изменение расстояния, в то время как значительное изменение возраста не оказывает на него практически никакого влияния.

Практический пример — цветы ириса

Для иллюстрации работы алгоритма кластеризации мы возьмем еще один классический датасет из библиотеки sklearn, а именно данные о цветах ириса.

датасет о цветах ириса из библиотеки sklearn

По традиции вначале откроем ноутбук к этому занятию⧉

Этап 1. Загрузка данных

Давайте сразу загрузим данные и преобразуем их в формат датафрейма из библиотеки Pandas.

# импортируем набор данных из модуля datasets библиотеки sklearn

from sklearn.datasets import load_iris

iris = load_iris()

# создаем датафрейм, берем данные из iris.data и название столбцов из iris.feature_names

iris_df = pd.DataFrame(iris.data, columns = iris.feature_names)

# смотрим первые пять значений

iris_df.head()

первые пять строк датасета о цветах ириса

1 2	# посмотрим на размерность iris_df.shape

(150, 4)

В данном случае речь идет о наборе данных, который состоит из 150 образцов цветов ириса, разделенных на три вида (Iris setosa, Iris virginica и Iris versicolor) по 50 растений в каждом. Каждый образец описан четырьмя атрибутами (длиной и шириной чашелистика и длиной и шириной лепестка).

Обратите внимание, мы сознательно не стали использовать целевую переменную, потому что решаем задачу кластеризации и предполагается, что мы не знаем заранее на какие группы или кластеры удастся разбить наши данные.

С другой стороны, тот факт, что нам заранее известно, что видов здесь три, поможет нам оценить качество кластерного анализа (об этом ниже).

Этап 2. Предварительная обработка данных

Для начала посмотрим, присутствуют ли пропущенные значения.

1	iris_df.isnull().sum()

sepal length (cm) 0

sepal width (cm) 0

petal length (cm) 0

petal width (cm) 0

dtype: int64

Мы видим, что пропущенных значений нет. Датасет был предварительно обработан.

Категориальных переменных у нас также нет. Это становится понятно из результата функции head().

Остается разобраться с масштабом признаков. Как уже было сказано, для метода k-средних нормализация данных имеет особое значение. Даже небольшое различие в масштабе признаков может повлиять на конечный результат.

# импортируем необходимый класс из модуля preprocessing библиотеки sklearn

from sklearn.preprocessing import StandardScaler

# создадим объект этого класса

scaler = StandardScaler()

# приведем данные к единому масштабу

iris_scaled = scaler.fit_transform(iris_df)

# заново создадим датафрейм с нормализованными значениями

iris_df_scaled = pd.DataFrame(iris_scaled, columns = iris.feature_names)

# посмотрим на первые пять строк

iris_df_scaled.round(2).head()

датасет о цветах ириса после нормализации

Этап 3 и 4. EDA и отбор признаков

Для целей кластерного анализа мы возьмем все имеющиеся у нас данные.

# оставим все признаки и для наглядности поместим наши данные в переменную Х

# целевой переменной у нас разумеется нет

X = iris_df_scaled

Этап 5.1. Обучение модели

Самый главный вопрос, который нам предстоит решить на этапе обучения модели заключается в выборе количества кластеров.

Количество кластеров в методе k-средних являтся так называемым гиперпараметром, то есть параметром, который нужно задать до обучения модели.

Мы усложним решаемую нами задачу и сделаем вид, что не обладаем экспертными знаниями о количестве видов ириса (на самом деле напомню, мы знаем, что их три). Значит нужно использовать метод локтя.

# импортируем нужный класс

from sklearn.cluster import KMeans

# создадим пустой список для записи показателя WCSS (нашей ошибки)

wcss = []

# воспользуемся новой для нас функцией range(), она возвращает последовательность чисел

# в данном случае числа от 1 до 10

for i in range(1, 11):

# настроим параметры модели (подробнее об этом расскажу чуть дальше)

kmeans = KMeans(n_clusters = i, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 42)

# обучим модель на наших данных с разным количеством кластеров

kmeans.fit(X)

# для каждого кластера рассчитаем ошибку (атрибут inertia_) и поместим в список

wcss.append(kmeans.inertia_)

# зададим размер график

plt.figure(figsize = (10,6))

# передадим функции plot() последовательность кластеров и ошибку WCSS

plt.plot(range(1, 11), wcss)

# и добавим подписи

plt.title('Выбор количества кластеров методом локтя')

plt.xlabel('Количество кластеров')

plt.ylabel('WCSS')

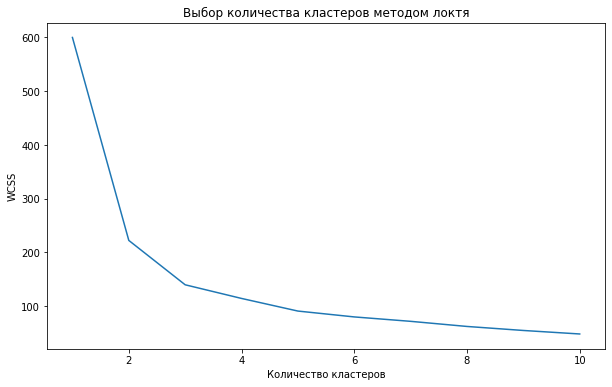
метод локтя в алгоритме k-средних на примере датасета о цветах ириса

Как видно на графике, когда мы перешли от трех до четырех кластеров, ошибка перестала существенно уменьшаться (это согласуется с тем, что видом действительно три).

Давайте создадим объект класса нашей модели, используя три кластера в качестве гипепараметра модели.

1 2	# заново обучим модель с тремя кластерами kmeans = KMeans(n_clusters = 3, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 42)

Подробнее рассмотрим параметры модели:

n_clusters: это количество кластеров, на которые мы хотим разбить наши наблюдения
init: определяет, как мы выберем первоначальное расположение (инициализацию) центроидов; есть два варианта, (1) выбрать центроиды случайно init = 'random' или (2) выбрать их так, чтобы центроиды с самого начала располагались максимально далеко друг от друга init = 'k-means++'; второй вариант оптимальнее
n_init: сколько раз алгоритм будет инициализирован, т.е. сколько раз будут выбраны центроиды до начала оптимизации; на выходе будет выбран тот вариант, где ошибка была минимальна
max_iter: максимальное количество итераций алгоритма после первоначального выбора центроидов
random_state: воспроизводимость результата, с этим мы уже знакомы

Обучим модель и сделаем прогноз:

1 2	# обучение и прогноз в данном случае можно сделать одним методом .fit_predict() y_pred = kmeans.fit_predict(X)

Этап 5.2. Оценка качества модели

Остается проверить качество модели и здесь возникает сложность. Ведь если при обучении с учителем у нас был критерий (целевая переменная), то здесь такого критерия нет.

Впрочем, так как у нас учебный датасет, и мы заранее знаем, к какому виду относится каждый цветок, то можем сравнить результат нашей модели с целевой переменной.

На настоящих данных такое конечно невозможно.

Вначале преобразуем нашу целевую переменную (iris.target) и наш прогноз (y_pred) в датафрейм (предварительно слегка их изменив, подробности в ноутбуке⧉).

# поместим переменные в словарь

d = {'Target' : iris.target, 'Prediction' : y_pred}

# превратим словарь в датафрейм с соответствующими названиями столбцов

df = pd.DataFrame(d, columns = ['Target', 'Prediction'])

С помощью функции where() создадим массив Numpy, в котором сравним каждую строчку датафрейма, и если целевая переменная и прогноз совпадают, зададим значение True, в противном случае — False.

comparison = np.where(df['Target'] == df['Prediction'], True, False)

print(type(comparison))

print(comparison[:5])

1 2	<class 'numpy.ndarray'> [ True True True True True]

Добавим этот массив в качестве столбца в датафрейм.

1 2	result['Comparison'] = comparison result.head()

Выведем долю совпавших (True) и не совпавших (False) значений. Для этого используем функцию value_counts(), которая подсчитает, сколько раз встречается каждое значение. Параметр normalize = True вернет относительное значение или процент. Ровно это нам и нужно.

1	df['Comparison'].value_counts(normalize = True).round(2)

True 0.83

False 0.17

Name: Comparison, dtype: float64

Как мы видим, модель была права в 83% случаев. Теперь давайте визуально оценим результат.

В исходном датафрейме четыре признака, а значит четыре измерения, столько мы представить графически не можем. Давайте возьмем первый (sepal length) и второй (sepal width) столбец исходного датафрейма.

Вначале построим точечную диаграмму целевой переменной.

# зададим размер

plt.figure(figsize = (10,6))

# возьмем первый и второй столбцы с помощью функции iloc()

# параметр с задаст каждой точке определенный код (0, 1, 2), а

# camp определит цвет каждой из точек

plt.scatter(X.iloc[:,0], X.iloc[:,1], c = iris.target, cmap = 'Paired')

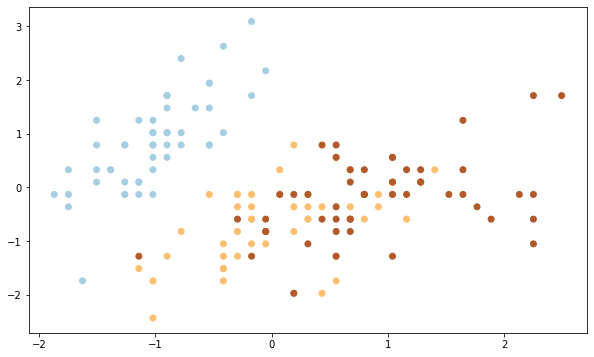
разделение на три вида цветов ириса: исходный датафрейм

Теперь посмотим на результат алгоритма кластеризации.

plt.figure(figsize = (10,6))

# снова построим точечную диаграмму, но коды точек возьмем из y_pred

plt.scatter(X.iloc[:,0], X.iloc[:,1], c = y_pred, cmap='Paired')

# кроме того выведем центроиды с помощью атрибута cluster_centers_

# зададим размер s = 150, красный цвет c = 'red', тип маркера - треугольник, и подпись

plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1], s = 150, c = 'red', marker = '^', label = 'Centroids')

# укажем, где разместить легенду

plt.legend(loc = 'upper right')

разделение на три вида цветов ириса: результат кластеризации

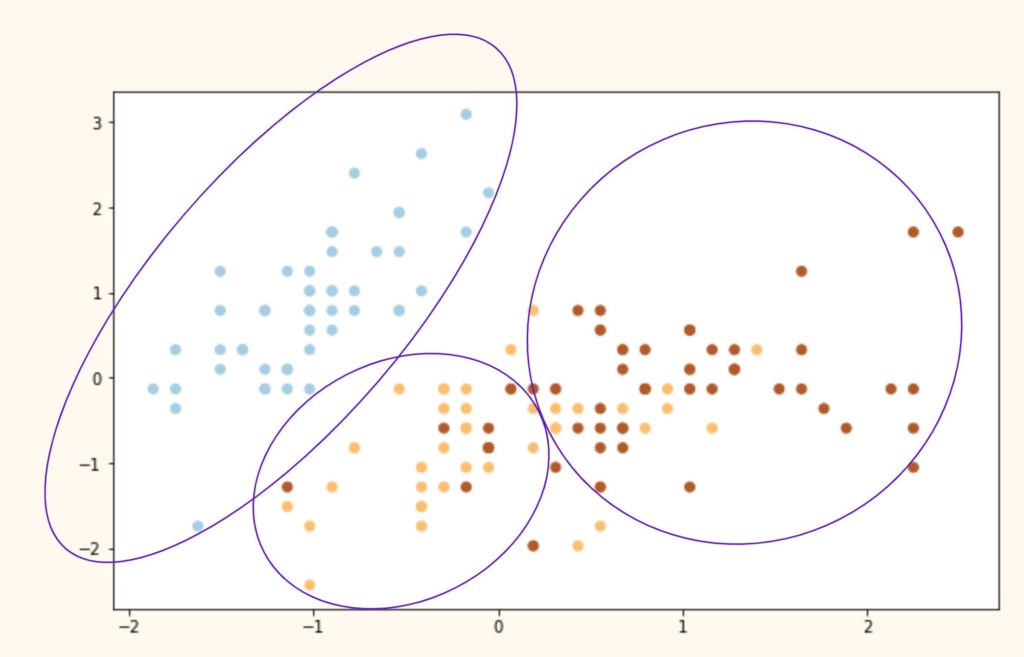
Выводы. Как мы видим, алгоритм идеально справился с кластером 0 (светлоголубой), однако допустил ошибки при разделение кластеров 1 и 2 (желтый и коричневый цвета). Почему?

На самом деле все дело в самом алгоритме. Как мы сказали выше, алгоритм группирует данные вокруг центроидов, а это значит, что он хорошо работает с выпуклыми и далеко расположенными друг от друга кластерами. Как только данные «проникают друг в друга» и расположены слишком близко, алгоритм теряется.

Иллюстрация ниже примерно показывает, что сделал алгоритм с нашими исходными видами и почему он ошибочно группировал некоторые точки.

пример важности выпуклости и отдаленности кластеров друг от друга для модели k-средних

Подведем итог

При решении задач кластеризации мы берем данные, обязательно их масштабируем и выбираем количество кластеров (с помощью экспертной оценки или метода локтя). К сожалению, дать точную оценку качества кластеризации бывает очень сложно из-за отсутствия разметки.

Вопросы для закрепления

Почему кластеризация называется машинным обучением без учителя?

Посмотреть правильный ответ

Ответ: в таких задачах отсутствует целевая переменная, разметка. Алгоритм пытается структурировать данные, о которых мало что известно заранее.

Как выбирается гиперпараметр модели (количество кластеров)?

Посмотреть правильный ответ

Ответ: существует два способа: (1) экспертное мнение и (2) метод локтя

В чем заключаются основные ограничения модели k-средних?

Посмотреть правильный ответ

Ответ: модель (1) очень чувствительна к масштабу признаков, и кроме того алгоритм предполагает (2) выпуклость и (3) разделенность данных

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

Мы закончили третий раздел классических алгоритмов машинного обучения. Пора переходить к более продвинутым задачам. Начнем с рекомендательных систем.

Ответы на вопросы

Вопрос. Скажите, а чем init = ‘k-means++’ лучше, чем init = ‘random’?

Ответ. Давайте разбираться. В первую очередь, посмотрим на случайную инициализацию центроидов ( init = 'random'). Как следует из самой формулировки, мы случайным образом выбираем центры кластеров, и затем алгоритм, как описано в лекции, старается минимизировать функцию потерь (WCSS в данном случае).

У такого подхода есть один недостаток. Если центры кластеров выбираются слишком близко друг к другу, то алгоритм может «разделить» то, что должно быть единым кластером, и «объединить» два разных. Пример ошибочной кластеризации на рисунке ниже.

инициализация центроидов случайным образом (init = 'random')

Как мы видим, алгоритм действительно минимизировал WCSS, однако лишь в пределах того, что ему позволил изначальный выбор положения центроидов. Это так называемый локальный минимум функции потерь. Глобальный же найден не был. Схематически глобальный минимум мог бы выглядеться как на графике ниже.

инициализация центроидов методом k-means++ (init = 'k-means++')

В данном случае глобальный оптимум был бы достигнут за счет максимизации изначального расстояния между центроидами. На этом и основан метод k-means++ ( init = 'k-means++').

Сам по себе алгоритм k-means++ очень прост:

Первый центроид выбирается случайно.
Далее рассчитывается Евклидово расстояние между этим центроидом и всеми остальными точками датасета. Наиболее удаленная точка станет следующим центроидом.
Каждая точка относится к ближайшему выбранному центроиду.
Точка, наиболее удаленная от «своего» центроида, становится следующим центром кластера.
Повторяем шаги 3 и 4 до тех пор, пока не выявим k центроидов.