Все курсы > Линейная алгебра > Занятие 6 (часть 2)
Продолжим на примере изучать фундаментальные подпространства матрицы.
Пример. Матрица инцидентности
Закон Ома и правило токов Кирхгофа
Для лучшего понимания последующего примера коротко приведем закон Ома и правило токов Кирхгофа для электрической цепи.
Закон Ома
В соответствии с законом Ома (Ohm’s law) сила тока (current) $I$ на участке цепи прямо пропорциональна напряжению (difference in potentials) $ \Delta V $ и обратно пропорциональна электрическому сопротивлению (resistance) $R$.
$$ I = \frac{\Delta V}{R} $$
Закон Ома можно выразить через проводимость (conductance) $C$, то есть величину обратную сопротивлению.
$$ C = \frac{1}{R} \rightarrow I = \Delta V C $$
Правило токов Кирхгофа
Одновременно правило токов Кирхгофа (Kirchhoff’s current law) утверждает, что алгебраическая сумма токов $I$ ветвей, сходящихся в каждом узле электрической цепи, равна нулю. При этом входящий в узел ток считается положительным, а исходящий — отрицательным.
$$ \sum^n_{j=1} I_j = 0 $$
Приведем пример.
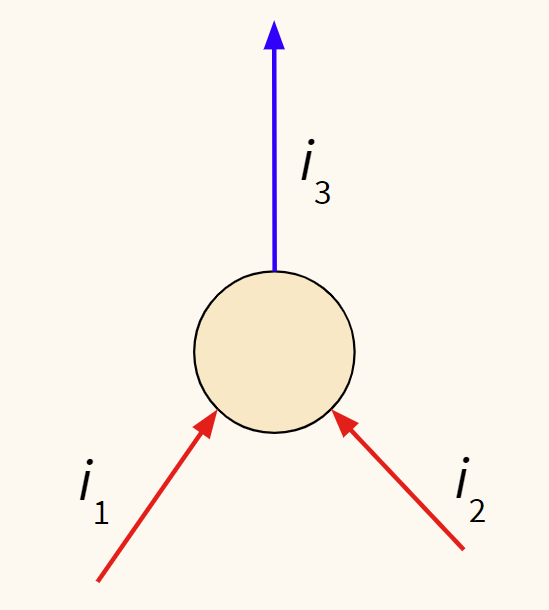
В примере выше $ i_1 + i_2 = i_3 $, и их сумма равна нулю.
Матрица инцидентности графа
Рассмотрим следующий орграф $D$, моделирующий электрическую цепь, в котором дугой будет участок цепи с одним и тем же током ($I$), а узлом — точка соединения ветвей, характеризующая потенциал электрического поля ($V$). Одновременно создадим матрицу инцидентности этого графа $A_D$.

В данном случае вершины будут столбцами, а строки — дугами. Таким образом, мы получаем матрицу $\underset{m \times n}{A}$ размерностью $5 \times 4$.
Замкнутый контур
Вначале рассмотрим подграф $S$ и соответствующую матрицу $B_S$. Такой граф представляет собой замкнутый контур.

Интересно, что в замкнутом контуре строки $(e_1+e_2=e_3)$ и столбцы $(v_2-v_3 = v_1)$ линейно зависимы.
Ядро матрицы
Вначале выполним умножение $ A \mathbf x $.
$$ A \mathbf x = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x_2-x_1 \\ x_3-x_2 \\ x_3-x_1 \\ x_4-x_1 \\ x_4-x_3 \end{bmatrix} $$
Поясним умножение вектора $\mathbf x$ на первую строку матрицы $A$.
$$ \begin{bmatrix} -1 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = -1x_1 + 1x_2 + 0x_3 + 0x_4 = x_2-x_1 $$
Заметим, что в уравнении выше вектор $ \mathbf x = \begin{bmatrix} x_1 & x_2 & x_3 & x_4 \end{bmatrix} $ характеризует потенциал ($V$) на узлах цепи, а вектор $A \mathbf x$ представляет собой разность этих потенциалов или напряжение ($\Delta V$).
Еще раз отметим, что ядро матрицы представляет собой такую комбинацию столбцов $A$, которая в результате превращает вектор $\mathbf x $ в нулевой вектор. Соответственно,
$$ A \mathbf x = \begin{bmatrix} x_2-x_1 \\ x_3-x_2 \\ x_3-x_1 \\ x_4-x_1 \\ x_4-x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} $$
Вектор $\mathbf x$, который будет решением $A \mathbf x = \mathbf 0$ равен
$$ \mathbf x = c \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} $$
Таким образом, ожидаемо, если потенциалы $V$ равны, а разницы потенциалов $\Delta V$ отсутствуют, то ток по цепи не потечет.
С точки зрения линейной алгебры заметим, что ранг $A$ и размернось ядра равны:
- $ r = 3 $
- $ dim(null(A)) = n-r = 4-3 = 1 $
Заземление
Обратите внимание, если заземлить, например, узел $v_4$, его потенциал будет равен нулю. Тогда, при $x_4 = 0$, четвертый столбец матрицы исчезнет и оставшиеся три столбца будут независимыми ($r=3$). Соответственно,
$$ A \mathbf x = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ 0 \end{bmatrix} = \begin{bmatrix} x_2-x_1 \\ x_3-x_2 \\ x_3-x_1 \\ -x_1 \\ -x_3 \end{bmatrix} $$
Как следствие, ни при каких значениях потенциалов напряжение не обратится в ноль (кроме $ \mathbf x = \mathbf 0 $, разумеется).
Более того, в данной матрице любые три столбца независимы, поэтому заземлить можно любой узел.
Коядро матрицы
Обратимся к коядру матрицы $A$ ($leftnull(A)$) или ядру $A^T$ ($null(A^T)$). Коядро матрицы является решением системы $\underset{n \times m}{A}^T \mathbf y = \mathbf 0$.
$$ \underset{4 \times 5}{A}^T \mathbf y = \begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} $$
$$ r = 3, dim(null(A^T)) = m-r = 5-3 = 2 $$
Умножим $A^T$ на $\mathbf y$.
$$ A^T \mathbf y = \begin{bmatrix} -y_1-y_3-y_4 \\ y_1-y_2 \\ y_2+y_3-y_5 \\ y_4+y_5 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} $$
Посмотрим, как согласуется найденное решение с графом (ребра $e_i$ для удобства переименуем в $y_i$).
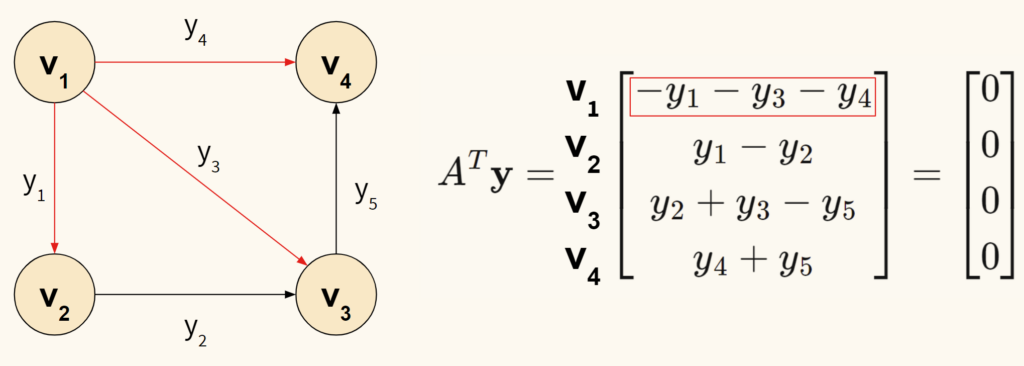
Посмотрим на первую строку. Выражение $-y_1-y_3-y_4$ характеризует исходящие токи из узла $v_1$ (аналогично для остальных узлов). В целом же $ A^T \mathbf y = \mathbf 0 $ описывает равновесие системы, при котором заряд не накапливается на узлах (в них он равен нулю). Другими словами, выполняется правило токов Кирхгофа.
Найдем решение $ A^T \mathbf y = \mathbf 0 $ без метода Гаусса. Как заряд может перемещаться по ребрам, не накапливаясь в узлах?
В частности, заряд может двигаться по «нижнему» подграфу между вершинами $v_1, v_2, v_3$. Тогда сила тока на соответствующих ребрах будет равна (обратите внимание, синяя стрелка при умножении на $-1$ сменила направление)

Аналогично, мы можем запустить ток по «верхнему» подграфу.

Что интересно, вектор, запускающий ток по большому кругу будет линейно зависимым (суммой предыдущих двух) и, как следствие, не будет входить в коядро матрицы $A$.

Физический смысл
Посмотрим на всю картину целиком. Выше мы сказали, что $ \mathbf x = \begin{bmatrix} x_1 & x_2 & x_3 & x_4 \end{bmatrix} $ характеризует потенциал сети ($V$), а $A \mathbf x$ — напряжение ($\Delta V$).
Добавим, что $ \mathbf y = \begin{bmatrix} y_1 & y_2 & y_3 & y_4 & y_5 \end{bmatrix} $ представляет собой силу тока $I$. При этом существует такая матрица $C$, которая превращает разность потенциалов в силу тока. Это матрица проводимости, и она определяется в соответствии с законом Ома.
Более того, решение $ A^T \mathbf y = \mathbf 0 $ соответствует правилу токов Кирхгофа.

В схеме выше не хватает внешнего источника питания. Предположим, что мы подаем ток на узел $v_1$, и из узла $v_4$ исходит ток такой же силы.

В этом случае сумма токов будет равна $A^T \mathbf y = f$. Тогда можно сказать, что
$$ \underset{V}{ \mathbf x} \rightarrow \underset{\Delta V}{A \mathbf x} \rightarrow \underset{I}{C A \mathbf x} \rightarrow \underset{f}{A^T C A \mathbf x} $$
Пространство строк
Остается найти пространство строк $A$ или пространство столбцов $A^T$. В $col(A^T)$ три столбца, а именно столбцы 1, 2, 4. На графе они соответствуют ребрам $e_1, e_2, e_4$, то есть тем ребрам, которые не образуют замкнутого контура.
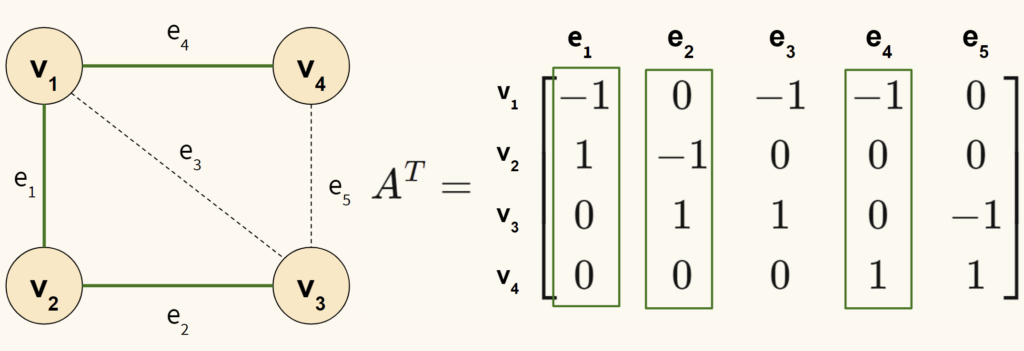
В теории графов такой (связный ациклический) граф называется деревом (tree).
Формула Эйлера для планарного графа
По формуле размерности коядра получаем
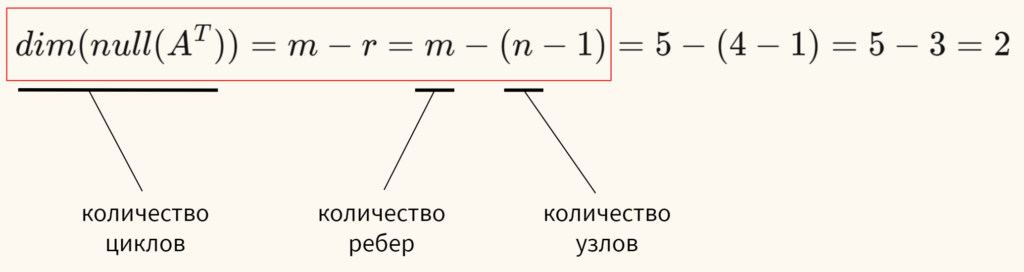
Перепишем это выражение.
$$ \underset{0D}{\text{количество узлов}}-\underset{1D}{\text{количество ребер}}+\underset{2D}{\text{количество циклов}} = 1 $$
Если заменить количество циклов на количество граней $F$ (faces) и учесть внешнюю грань (пространство за пределами графа), то получается формула Эйлера (Euler’s formula) для планарного графа $G$
$$ |V(G)|-|E(G)|+|F(G)| = 2 $$
Подведем итог
В первой части занятия мы познакомились с рангом и четырьмя фундаментальными подпространствами матрицы, а также с тем, как эти понятия связаны с векторными пространствами, линейными преобразованиями, системой линейных уравнений и определителем матрицы.
Во второй части мы рассмотрели, как матрица и ее фундаментальные подпространства помогают лучше понять физические процессы.
Перейдем к изучению метода наименьших квадратов.