Продолжим работу в том же ноутбуке⧉
Масштабирование признаков
Рассмотрим линейную регрессию с двумя независимыми переменными, у которых совершенно разный масштаб. Например, один признак находится в диапазоне от 0 до 1000, а второй — от 0 до 1. Логично, что чтобы подстроиться под такие признаки, модель выберет небольшой первый и большой второй коэффициенты.
Проблема такой модели в том, что на этапе обучения скорость оптимизации таких коэффициентов (весов, параметров) не будет одинаковой.
На графике изолиний (как бы «вид сверху») функция потерь такой модели примет эллиптическую форму (по оси x соответственно будет отложен признак с небольшим диапазоном, по оси y — с большим).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
def paraboloid_countours(min, max, a = 1, b = 1, w1_list = None, w2_list = None): # установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -10 до 10 # для осей w1 и w2 w1_plot = np.arange(min, max, 0.02) w2_plot = np.arange(min, max, 0.02) # создадим координатную плоскость из осей w1 и w2 w1_plot, w2_plot = np.meshgrid(w1_plot, w2_plot) f = (w1_plot ** 2)/a + (w2_plot ** 2)/b # построим изолинии (линии уровня) ax.contourf(w1_plot, w2_plot, f, cmap = 'Blues') # если функции передали списки весов, выведем траекторию их обновления if w1_list != None and w2_list != None: ax.plot(w1_list, w2_list, c = 'red') # укажем подписи к осям ax.set_xlabel('w1', fontsize = 15) ax.set_ylabel('w2', fontsize = 15) # создадим сетку в виде прерывистой черты plt.grid(linestyle = '--') # выведем результат plt.show() |
|
1 |
paraboloid_countours(-20, 20, 1, 5) |

При использовании алгоритма градиентного спуска мы в первую очередь найдем две частные производные этой функции и подберем единый для обеих производных коэффициент скорости обучения. Так как масштаб признаков будет различным, на каждой итерации мы будем получать существенно различающиеся значения градиента для разных направлений.
Пропишем функцию потерь и найдем ее частные производные.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# пропишем функцию потерь # переменные a и b будут определять масштаб каждого из признаков def objective(w1, w2, a, b): return (w1 ** 2) / a + (w2 ** 2) / b # а также производную по первой def partial_1(w1, a): return (2.0 * w1) / a # и второй переменным def partial_2(w2, b): return (2.0 * w2) / b |
Попробуем найти оптимальные веса с помощью алгоритма градиентного спуска.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def paraboloid_gd(w1, w2, a, b, iter = 100, learning_rate = 0.025): # создадим списки для учета весов и уровня ошибки w1_list, w2_list, l_list = [], [], [] # в цикле с заданным количеством итераций for i in range(iter): # будем добавлять текущие веса в соответствующие списки w1_list.append(w1) w2_list.append(w2) # и рассчитывать и добавлять в список текущий уровень ошибки l_list.append(objective(w1, w2, a, b)) # также рассчитаем значение частных производных при текущих весах par_1 = partial_1(w1, a) par_2 = partial_2(w2, b) # будем обновлять веса в направлении, # обратном направлению градиента, умноженному на скорость обучения w1 = w1 - learning_rate * par_1 w2 = w2 - learning_rate * par_2 # выведем итоговые веса модели и значение функции потерь return w1_list, w2_list, l_list |
|
1 2 |
w1_list, w2_list, l_list = paraboloid_gd(15, 15, 1, 5) w1_list[-1], w2_list[-1], l_list[-1] |
|
1 |
(0.09348204032106357, 5.545944564745904, 6.1602391149095155) |
Вновь выведем изолинии функции потерь, дополнив их траекторией изменения весов признаков.
|
1 |
paraboloid_countours(-20, 20, 1, 5, w1_list, w2_list) |
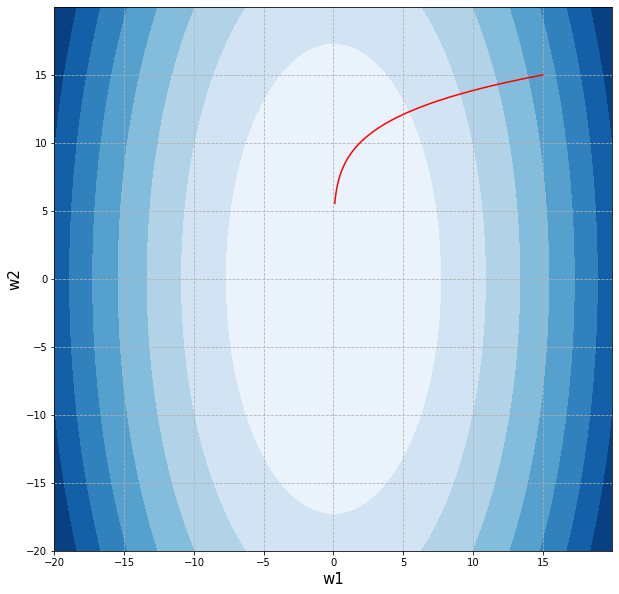
Мы не смогли дойти до минимума. Для иллюстрации этой особенности можно также вывести графики изменения весов в процессе обучения алгоритма.
|
1 2 3 |
plt.plot(w1_list) plt.plot(w2_list) plt.show() |
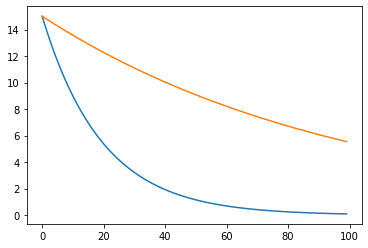
Посмотрим, что будет, если привести признаки к одному масштабу. Вначале найдем минимум методом градиентного спуска.
|
1 2 3 |
# напомню, параметры a и b в данном случае контролируют масштаб признаков w1_list, w2_list, l_list = paraboloid_gd(15, 15, 1, 1) w1_list[-1], w2_list[-1], l_list[-1] |
|
1 |
(0.09348204032106357, 0.09348204032106357, 0.017477783725177908) |
Выведем результат на графике.
|
1 |
paraboloid_countours(-20, 20, 1, 1, w1_list, w2_list) |

Посмотрим на обновления весов.
|
1 2 3 |
plt.plot(w1_list) plt.plot(w2_list) plt.show() |
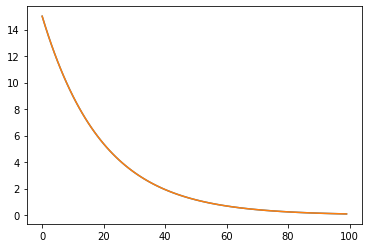
Мы видим только оранжевую линию, потому что одна кривая перекрывает другую.
Полиномиальная регрессия
Данные далеко не всегда хорошо аппроксимируются прямой линией. Создадим искусственный набор данных.
|
1 2 3 |
np.random.seed(42) X = np.random.normal(2, 4, 50) y = 2 * X ** 2 + 2 * X + 50 + np.random.normal(3, 10, 50) |
|
1 2 3 |
plt.figure(figsize = (8, 6)) plt.scatter(X, y) plt.show() |

Попробуем «наложить» на данные модель линейной регрессии.
|
1 2 3 4 5 |
from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X.reshape(-1, 1), y) y_pred = model.predict(X.reshape(-1, 1)) |
Посмотрим на получившиеся коэффициенты.
|
1 |
model.coef_, model.intercept_ |
|
1 |
(array([7.65521764]), 76.7171405919949) |
Выведем результат на графике и оценим качество через RMSE и $R^2$.
|
1 2 3 4 |
plt.figure(figsize = (8, 6)) plt.scatter(X, y) plt.plot(X, y_pred, color='r') plt.show() |

|
1 2 3 |
from sklearn.metrics import mean_squared_error, r2_score mean_squared_error(y, y_pred, squared = False), r2_score(y, y_pred) |
|
1 |
(34.5483663960937, 0.40159428156318455) |
В данном случае очевидно, что данные гораздо более удачно моделировать с помощью квадратичной функции (quadratic function).
$$ \hat{y} = \theta_0 + \theta_1x \theta_2x^2 $$
Обратите внимание, что в квадрат возводится не коэффициент $\theta$, а признак $x$. Поэтому все, что нам нужно, это создать еще один признак, равный квадрату исходного признака. Для этого в sklearn есть класс PolynomialFeatures.
|
1 2 3 4 |
from sklearn.preprocessing import PolynomialFeatures polynomial_features = PolynomialFeatures(degree = 2, include_bias = False) X_poly = polynomial_features.fit_transform(X.reshape(-1, 1)) |
Параметр include_bias регулирует добавлять ли столбец из единиц для свободного коэффициента или нет. Так как в данном случае мы используем класс LinearRegression, который сам рассчитывает все коэффициенты, такой столбец нам не понадобится.
|
1 2 |
# сравним исходный признак X[:5] |
|
1 |
array([3.98685661, 1.4469428 , 4.59075415, 8.09211943, 1.0633865 ]) |
|
1 2 |
# с новыми X_poly[:5] |
|
1 2 3 4 5 |
array([[ 3.98685661, 15.89502565], [ 1.4469428 , 2.09364345], [ 4.59075415, 21.07502369], [ 8.09211943, 65.4823968 ], [ 1.0633865 , 1.13079085]]) |
Второй столбец — квадрат первого.
|
1 |
3.98685661 ** 2 |
|
1 |
15.89502562870069 |
|
1 |
X.shape, X_poly.shape |
|
1 |
((50,), (50, 2)) |
Построим модель.
|
1 2 3 4 5 6 |
model = LinearRegression() model.fit(X_poly, y) y_poly_pred = model.predict(X_poly) model.coef_, model.intercept_ |
|
1 |
(array([2.31100218, 1.98024538]), 53.13013943148053) |
|
1 2 3 4 5 6 7 8 9 10 11 |
import operator sort_axis = operator.itemgetter(0) sorted_zip = sorted(zip(X, y_poly_pred), key = sort_axis) X_plot, y_poly_pred_plot = zip(*sorted_zip) plt.figure(figsize = (8, 6)) plt.plot(X_plot, y_poly_pred_plot, color = 'r') plt.scatter(X, y) plt.show() |

|
1 |
mean_squared_error(y, y_poly_pred, squared = False), r2_score(y, y_poly_pred) |
|
1 |
(8.596303829633031, 0.9629520471499875) |
Два важных замечания.
(1) Масштабирование признаков становится особенно важным при оптимизации методом градиентного спуска (потому что, например, если мы возводим признак в квадрат, его диапазон также увеличивается).
(2) Функция не обязательно должна быть степенной, если нам нужно например предсказать данные которые растут, но затем выходят на плато (например, цены) можно использовать квадратный корень.