Модуль random. Часть 4 | Программирование на Питоне

Все курсы > Программирование на Питоне > Занятие 10 (часть 4)

Рассмотрим способы расчета комбинаций с помощью Питона. Помимо модуля random рассмотрим модуль itertools.

Содержание занятия

Комбинаторика в Питоне
- np.random.shuffle() и np.random.permutation()
- Модуль itertools
  - Перестановки
    - Перестановки без замены
    - Перестановки с заменой
  - Сочетания
Подведем итог
- Вопросы для закрепления
- Ответы на вопросы

Комбинаторика в Питоне

np.random.shuffle() и np.random.permutation()

Обе эти функции перемешивают (shuffle) или переставляют (permute) элементы списка или массива. Основное отличие заключается в том, что np.random.shuffle() изменяет исходный массив, а np.random.permutation() создает «перемешанную» копию исходного массива:

# создадим массив и передадим его в функцию np.random.shuffle()

arr = np.array([1, 2, 3, 4, 5])

# сама функция выдала None, исходный массив при этом изменился

print(np.random.shuffle(arr), arr)

1	None [3 2 1 5 4]

# еще раз создадим массив

arr = np.array([1, 2, 3, 4, 5])

# передав его в np.random.permutation(),

# мы получим перемешанную копию и исходный массив без изменений

np.random.permutation(arr), arr

1	(array([2, 4, 3, 1, 5]), array([1, 2, 3, 4, 5]))

Перемешивание массива можно использовать, если, например, нужно внести элемент случайности в работу с данными. Давайте создадим аналог функции train_test_split() библиотеки sklearn, которой мы пользовались для разделения выборки на обучающую и тестовую части.

# объявим функцию, которая принимает признаки X и целевую переменную y в формате

# массива Numpy или датафрейма

# дополнительно пропишем размер тестовой выборки с параметром по умолчанию 0,3

# и возможностью задать точку отсчета

def split_data(X, y, test_size = 0.3, random_state = None):

# проверим является ли X массивом Numpy с помощью функции isinstance()

if isinstance(X, np.ndarray):

# если да, превратим в датафрейм

X = pd.DataFrame(X)

# сделаем то же самое для y

if isinstance(y, np.ndarray):

y = pd.DataFrame(y)

# еще один способ выполнить такую проверку

# if type(X). __module__ == np. __name__:

# X = pd.DataFrame(X)

# if type(y). __module__ == np. __name__:

# y = pd.DataFrame(y)

# установим точку отсчета

np.random.seed(random_state)

# перемешаем индексы строк датасета X, не изменяя исходный массив

indices = np.random.permutation(len(X))

# определим количество строк, которые войдут в тестовую выборку

# для этого умножим количество строк в X на долю тестовой выборки

data_test_size = int(X.shape[0] * test_size)

# начиная с этого количества (границы) будет обучающая выборка

train_indices = indices[data_test_size:]

# перед ним, тестовая

test_indices = indices[:data_test_size]

# с помощью метода .iloc() найдем в X все строки,

# соответствующие индексам в переменных train_indices и test_indices

X_train = X.iloc[train_indices]

X_test = X.iloc[test_indices]

# сделаем то же самое для y

y_train = y.iloc[train_indices]

y_test = y.iloc[test_indices]

# выведем выборки в том порядке, в котором они выводятся в sklearn

return X_train, X_test, y_train, y_test

Подгрузим данные о пациентах с диабетом из модуля datasets библиотеки sklearn. Как это делается, мы подробно разобрали на занятии по линейной регрессии на вводном курсе.

# импортируем данные о пациентах с диабетом

from sklearn.datasets import load_diabetes

# помещаем их в переменную data

data = load_diabetes()

# создаем два датафрейма

X = pd.DataFrame(data.data, columns = data.feature_names)

y = pd.DataFrame(data.target, columns = ['target'])

# для проверки работы функции можно также создать массивы Numpy

# X = data.data

# y = data.target

Вызовем созданную функцию и проверим ее работу.

1	X_train, X_test, y_train, y_test = split_data(X, y, random_state = 42)

Теперь проверим, правильно ли записались данные в созданные выше переменные и расположены ли в них строки в случайном порядке.

1	X_train.head(3)

функция для разделения выборки на обучающую и тестовую части

1	y_train.head(3)

функция для разделения выборки на обучающую и тестовую части 2

Похоже, что все работает как надо.

Модуль itertools

Рассмотренные выше функции не позволяют вывести все возможные комбинации элементов. Для этого есть модуль itertools.

Перестановки

Напомню, что перестановка (permutation) в комбинаторике позволяет узнать, сколькими способами можно разместить элементы множества в определенном порядке.

Перестановки без замены

Вначале возьмем те случаи, когда один элемент может повторяться только один раз. В этом случае мы говорим о перестановках без замены (permutations without replacement). Они бывают двух видов: без повторений и с повторениями.

Перестановки без повторений

Рассмотрим простой пример. У нас есть три элемента A, B и C. Сколькими способами можно переставить эти объекты так, чтобы порядок элементов не повторялся?

Так как элементы в исходном множестве не повторяются, то такая перестановка называется перестановкой без повторения (permutation without repetition).

Очевидно, на первое место мы можем поставить любой из трех элементов, на второе только оставшиеся два, на третьем месте окажется только один элемент. Получается 3 x 2 x 1 = 6. Такой расчет не что иное, как факториал числа три (3!).

$$ P(n) = n! \rightarrow P(3) = 3! = 6 $$

На Питоне мы можем вычислить факториал нужного нам числа через функцию factorial() модуля math.

# импортируем модуль math

import math

# передадим функции factorial() число 3

math.factorial(3)

Кроме того, мы можем воспользоваться функцией permutations() модуля itertools. В этом случае мы можем вывести все возможные перестановки элементов множества.

# импортируем модуль itertools

import itertools

# создадим строку из букв A, B, C

x = 'ABC'

# помимо строки можно использовать и список

# x = ['A', 'B', 'C']

# и передадим ее в функцию permutations()

# так как функция возвращает объект itertools.permutations,

# для вывода результата используем функцию list()

list(itertools.permutations(x))

[('A', 'B', 'C'),

('A', 'C', 'B'),

('B', 'A', 'C'),

('B', 'C', 'A'),

('C', 'A', 'B'),

('C', 'B', 'A')]

Если все же нас интересуют не сами перестановки, а их количество, можно воспользоваться функцией len().

1	len(list(itertools.permutations(x)))

Размещения

Приведем чуть более сложный пример. Предположим, в соревнованиях учавствуют шесть команд (n = 6), и нам нужно узнать, сколькими способами эти команды могут занять первое, второе и третье призовые места. Просто вычислить факториал мы уже не можем, нам нужно уменьшить общее число вариантов на то количество перестановок, которое не будет реализовано, потому что мест всего три (r = 3).

Такой тип перестановок называют размещением (partial permulation). Приведем формулу.

$$ P(n, r) = \frac{n!}{(n-r)!} \rightarrow P(6, 3) = \frac{6!}{(6-3)!} = 120 $$

На Питоне мы можем применить ту же функцию permutations(), передав ей через параметр r размер выборки (количество мест).

# теперь элементов исходного множества шесть

x = 'ABCDEF'

# чтобы узнать, сколькими способами их можно разместить на трех местах,

# передадим параметр r = 3 и выведем первые пять элементов

list(itertools.permutations(x, r = 3))[:5]

[('A', 'B', 'C'),

('A', 'B', 'D'),

('A', 'B', 'E'),

('A', 'B', 'F'),

('A', 'C', 'B')]

Посмотрим на общее количество перестановок.

1 2	# как и в предыдущем случае, воспользуемся функцией len() len(list(itertools.permutations(x, r = 3)))

120

Дополнительно замечу, что в случае если выборка r также велика, как и множество n (первый пример), то формулу размещения можно записать как

$$ P(n, n) = \frac{n!}{(n-n)!} $$

В знаменателе получается 0!, и для того чтобы избежать деления на ноль, принято считать, что факториал нуля равен единице (0! = 1).

Перестановки с повторениями

Давайте дополнительно усложним задачу и рассчитаем количество перестановок букв в слове «молоко». В данном случае мы не можем воспользоваться факториалом, потому что буква «о» повторяется трижды, и соответственно мы можем разместить ее 3! способами. Как следствие, для получения правильного ответа нам нужно разделить количество перестановок на шесть (3! = 6).

В таком случае мы говорим про перестановки с повторениями (permutations with repetitions).

$$ \frac{6!}{3!} = 120 $$

В целом, если какой-то из элементов повторяется, то общее число перестановок нужно разделить на произведение факториалов повторяющихся элементов (правильнее сказать на произведение факториалов повторяемости каждого элемента, однако факториал неповторяющихся элементов равен 1! = 1, поэтому ими можно пренебречь).

$$ \frac{P(n, r)}{n_1! \cdot n_2! \cdot … \cdot n_r!}, \text{где } n_1! + n_2! + … + n_r! = n $$

Для расчета перестановок с повторениями напишем собственную функцию.

# импортируем необходимые библиотеки

import itertools

import numpy as np

import math

# объявим функцию permutations_w_repetition(), которая будет принимать два параметра

# x - строка, список или массив Numpy

# r - количество мест в перестановке, по умолчанию равно количеству элементов в x

def permutations_w_repetition(x, r = len(x)):

# если передается строка,

if isinstance(x, str):

# превращаем ее в список

x = list(x)

# в числителе рассчитаем количество перестановок без повторений

numerator = len(list(itertools.permutations(x, r = r)))

# для того чтобы рассчитать знаменатель найдем,

# сколько раз повторяется каждый из элементов

_, counts = np.unique(x, return_counts = True)

# объявим переменную для знаменателя

denominator = 1

# и в цикле будем помещать туда произведение факториалов

# повторяющихся элементов

for c in counts:

# для этого проверим повторяется ли элемент

if c > 1:

# и если да, умножим знаменатель на факториал повторяющегося элемента

denominator *= math.factorial(c)

# разделим числитель на знаменатель

# деление дает тип float, поэтому используем функцию int(),

# чтобы результат был целым числом

return int(numerator/denominator)

Рассчитаем количество перестановок с повторениями букв в слове «молоко».

# создадим строку со словом "молоко"

x = 'МОЛОКО'

# вызовем функцию

permutations_w_repetition(x)

120

Перестановки с заменой

Перестановки с заменой (permutations with replacement), когда элементы могут использоваться более одного раза, есть не что иное, как прямое или декартово произведение множества само на себя.

Вначале рассмотрим суть декартова произведения.

Декартово произведение (Cartesian product) двух множеств предполагает, что мы создаем все возможные упорядоченные пары исходных множеств.

В частности, если у нас есть одно множество A с элементами {1, 2, 3} и множество B с элементами {x, y}, то их произведением A x B будут все возможные упорядоченные комбинации этих элементов.

При умножении множества само на себя один раз мы говорим про квадрат Декарта (Cartesian square). В частности, если умножить множество действительных чисел R само на себя (R x R), то получится координатная плоскость или декартова система координат (Cartesian plane).

координатная плоскость или декартова система координат

Замечу, что множество можно умножить само на себя много раз, в этом случае говорят про декартову степень (Cartesian power).

Так вот, перестановка с заменой и есть декартова степень исходного множества.

Например, представим, что в кафе есть два сорта мороженого, ванильное и клубничное, и мы можем заказать любые два шарика. В частности, два шарика ванильного или два шарика клубничного. Тогда возможные варианты заказа можно представить следующим образом.

При этом так как это перестановки и порядок имеет значение, (клубника, ваниль) и (ваниль, клубника) это разные блюда.

В модуле itertools для такой операции есть функция product().

1 2	# посмотрим, сколькими способами можно выбрать два сорта мороженого list(itertools.product(['Ваниль', 'Клубника'], repeat = 2))

[('Ваниль', 'Ваниль'),

('Ваниль', 'Клубника'),

('Клубника', 'Ваниль'),

('Клубника', 'Клубника')]

В целом формула прямого произведения выглядит как n^r. Например, если во множестве четыре элемента, то поставить два элемента из этих четырех можно шестнадцатью способами (4² = 16).

1 2	# посмотрим на способы переставить с заменой два элемента из четырех list(itertools.product('ABCD', repeat = 2))

[('A', 'A'),

('A', 'B'),

('A', 'C'),

('A', 'D'),

('B', 'A'),

('B', 'B'),

('B', 'C'),

('B', 'D'),

('C', 'A'),

('C', 'B'),

('C', 'C'),

('C', 'D'),

('D', 'A'),

('D', 'B'),

('D', 'C'),

('D', 'D')]

Убедимся, что таких способов 16.

1	len(list(itertools.product('ABCD', repeat = 2)))

В данном случае мы умножаем множество само на себя два раза.

умножение множества само на себя два раза

Замечу, что если умножать множество на себя три раза, то графически понадобился бы куб. Резюмируем все изученные способы перестановок на схеме ниже.

Сочетания

Сочетания без повторений

В отличие от перестановок при расчете сочетаний (combinations) порядок значения не имеет. Например, представьте, что в парном теннисе из пяти кандидатов нам нужно собрать команду из двух человек.

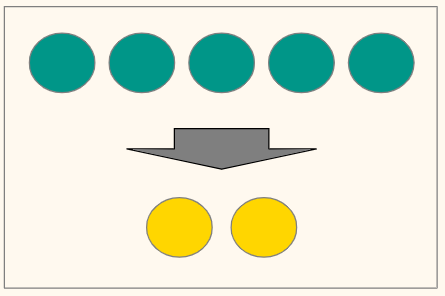
По сравнению с похожей задачей с призовыми местами, нам не важно кто будет первым, а кто вторым и если считать через перестановки, то получится так

$$ P(5, 2) = \frac{5!}{(5-2)!} = 20 $$

Для наглядности посмотрим на эти комбинации с помощью Питона.

# возьмем пять элементов

x = 'ABCDE'

# и найдем способ переставить два элемента из этих пяти

list(itertools.permutations(x, r = 2))

[('A', 'B'),

('A', 'C'),

('A', 'D'),

('A', 'E'),

('B', 'A'),

('B', 'C'),

('B', 'D'),

('B', 'E'),

('C', 'A'),

('C', 'B'),

('C', 'D'),

('C', 'E'),

('D', 'A'),

('D', 'B'),

('D', 'C'),

('D', 'E'),

('E', 'A'),

('E', 'B'),

('E', 'C'),

('E', 'D')]

Однако обратите внимание, некоторые комбинации, если не учитывать порядок, повторяются (например, AB и BA). Поэтому сочетаний (то есть перестановок без учета порядка) меньше. Причем меньше на количество перестановок каждого типа, то есть r!. В данном случае перестановок каждого типа два, то есть 2! = 2.

1	int(len(list(itertools.permutations(x, r = 2)))/math.factorial(2))

Выведем формулу.

$$ C(n, r) = \frac{n!}{(n-r)! r!} \rightarrow C(5, 2) = \frac{5!}{(5-2)! 2!} = 10 $$

В Питоне для сочетаний есть удобная функция combinations().

1	list(itertools.combinations(x, 2))

[('A', 'B'),

('A', 'C'),

('A', 'D'),

('A', 'E'),

('B', 'C'),

('B', 'D'),

('B', 'E'),

('C', 'D'),

('C', 'E'),

('D', 'E')]

1	len(list(itertools.combinations(x, 2)))

Сочетания с повторениями

Если допустить повторение элементов, сочетаний станет больше.

1	list(itertools.combinations_with_replacement('AB', 2))

1	[('A', 'A'), ('A', 'B'), ('B', 'B')]

В целом количество сочетаний с повторениями (combinations with repetitions или иногда with replacement) вычисляется по следующей формуле.

$$ C(n, r)_{rep} = \frac{(n+r-1)!}{(n-r)! r!} $$

В нашем случае,

$$ C(2, 2)_{rep} = \frac{(2+2-1)!}{(2-2)! 2!} = \frac{3!}{2!} = 3 $$

Биномиальные коэффициенты

Давайте вернемся к биномиальному распределению и его функции вероятности. Напомню, что во втором примере мы три раза подбрасывали монету (n = 3), вероятность выпадения орла составляла 0,7 (p = 0,7), а найти мы должны были выпадение двух орлов (k = 2).

$$ P(X = k) = C(n, k) p^k (1-p)^{n-k} $$

$$ P(X = 2) = C(3, 2) \times 0,7^2 \times (1-0,7)^{3-2} = 3 \times 0,7^2 \times 0,3^1 = 0,441 $$

Первая часть этой формулы и есть количество сочетаний при выпадении двух орлов в трех бросках. Для того чтобы вывести дерево вероятностей мы можем воспользоваться декартовой степенью множества {решка, орел} или {H, T}.

1 2	# трижды умножим множество {H, T} само на себя list(itertools.product('HT', repeat = 3))

[('H', 'H', 'H'),

('H', 'H', 'T'),

('H', 'T', 'H'),

('H', 'T', 'T'),

('T', 'H', 'H'),

('T', 'H', 'T'),

('T', 'T', 'H'),

('T', 'T', 'T')]

Само же количество сочетаний рассчитаем через функцию combinations().

# посмотрим, в скольких комбинациях выпадет две решки при трех бросках

comb = len(list(itertools.combinations('ABC', 2)))

comb

Полный расчет на Питоне будет выглядеть вот так.

1	round(comb * (0.7 ** 2 * (1 - 0.7)** (3 - 2)), 3)

0.441

Конечно же этот результат гораздо проще получить через библиотеку scipy.

1	binom.pmf(k = 2, n = 3, p = 0.7).round(3)

0.441

Подведем итог

По большому счету мы затронули три важные темы:

Моделирование и исследование случайных процессов с помощью модуля random;
Распределения (дискретные и непрерывные) случайных величин; и
Комбинаторику на Питоне.

Пройденный материал поможет как в дальнейшем изучении теории, так и в построении более качественных моделей машинного обучения.

Вопросы для закрепления

Вопрос. Чем теоретическая вероятность отличается от эмпирической?

Посмотреть правильный ответ

Ответ: теоретическая вероятность — это соотношение благоприятствующих событию исходов ко всем возможным исходам испытания, эту вероятность мы можем рассчитать; эмпирическая вероятность — соотношение наступления события к общему числу испытаний, которое мы наблюдаем в результате эксперимента

Вопрос. Чем отличается функция вероятности (probability mass function, pmf) от плотности вероятности (probability density function, pdf)?

Посмотреть правильный ответ

Ответ: функция вероятности задает распределение дискретной случайной величины (discrete random variable), а плотность вероятности описывает распределение непрерывной величины (discrete random variable)

Вопрос. Чем сочетания отличаются от перестановок?

Посмотреть правильный ответ

Ответ: при расчете количества перестановок мы учитываем порядок, в котором располагаются элементы, при расчете количества сочетаний порядок не важен.

В конце ноутбука приведены дополнительные упражнения⧉.

На следующем занятии мы немного отдохнем от математики и рассмотрим объектно-ориентированный подход к программированию.

Ответы на вопросы

Вопрос. Подскажите, а зачем повторно импортировать Numpy, itertools и math перед объявлением собственной функции permutations_w_repetition()? Ведь вы уже импортировали их перед этим.

Ответ. Я повторно импортировал необходимые библиотеки на случай использования функции в других проектах. Предположим, вы захотите использовать эту функцию в своей работе и поместите ее в отдельный файл. Для того чтобы код сработал, вам сначала понадобится импортировать эти три библиотеки.

Дополнительно замечу, что Руководство по написанию кода на Питоне (Python Enhancement Proposal или PEP 8) рекомендует⧉ делать импорт необходимых библиотек и модулей «после комментариев к модулю и строк документации, и перед объявлением констант», а не внутри функций или классов. Подробнее об этом мы поговорим через одно занятие.

Вопрос. Скажите, а чем матожидание отличается от среднего значения?

Ответ. Матожидание (expected value) — это то среднее значение, которое мы предполагаем/ожидаем получить с учетом известного нам типа распределения. Например, зная, что случайная величина следует биномиальному распределению с параметрами n = 3 и p = 0,7, мы ожидаем наблюдать среднее значение np = 3 x 0,7 = 2,1. В частности, с помощью функции scipy.stats.binom.stats() мы рассчитываем именно матожидание распределения.

Собрав же фактические данные (мы для этого использовали модуль random и функцию np.random.binomial()), мы можем посмотреть насколько среднее (mean value) этих данных согласуется с математическим ожиданием. При достаточно большом количестве экспериментов среднее должно стремиться к математическому ожиданию.

Привел пример в конце ноутбука⧉.