Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
- Бинарная логистическая регрессия
- Мультиклассовая логистическая регрессия
- Подведем итог
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
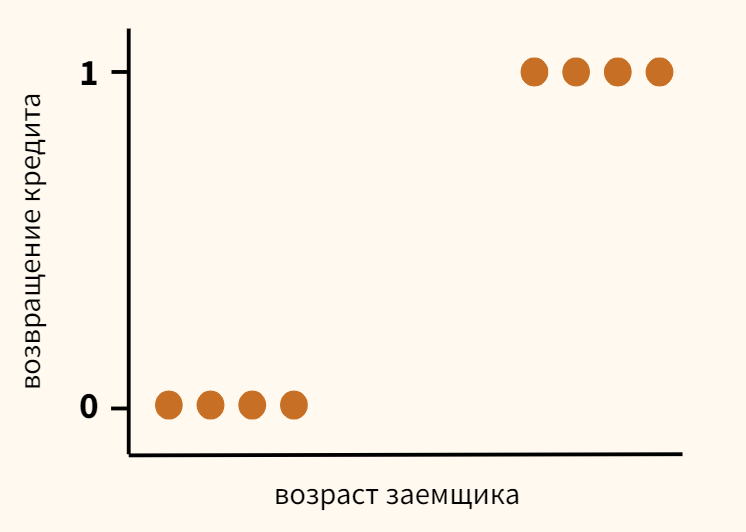
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.

- Если $ f_w(x) < 0,5 \rightarrow \hat{y} = 0 $
- Если $ f_w(x) \geq 0,5 \rightarrow \hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
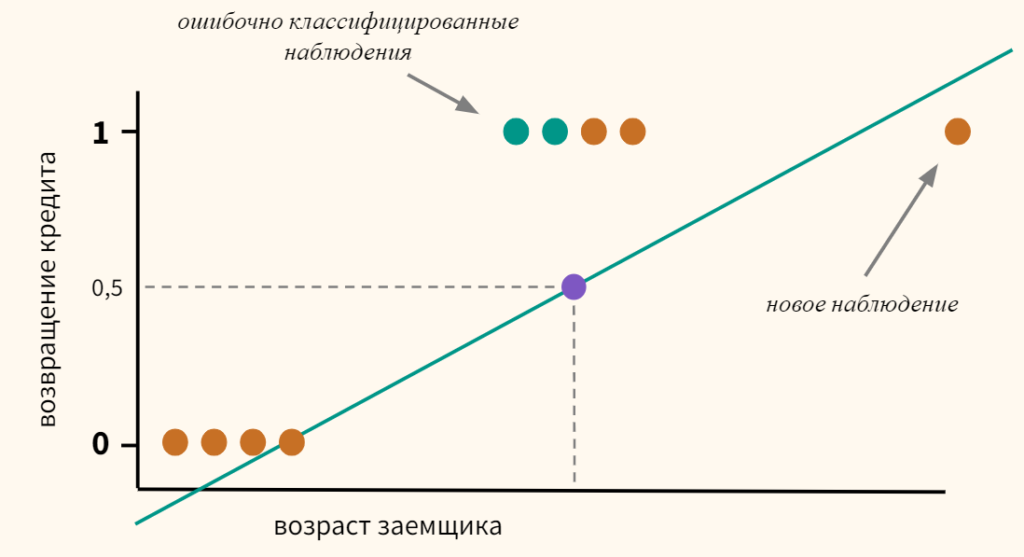
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможное решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 \leq h(x) \leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = \frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} \approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} \approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = X\theta \rightarrow h_{\theta}(x) = \frac{1}{1+e^{-(X\theta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия» нет. Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $\theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
1 2 3 |
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(-z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{\theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{\theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $\theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{\theta}(x) = P(y = 1 | x; \theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $\theta$ (probability of y = 1 given x, parameterized by $\theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; \theta) = 1-P(y = 1 | x; \theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{\theta}(x) \geq 0,5 $$
$$ y = 0, h_{\theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z \geq 0 $, а так как $ z = X\theta $, то можно сказать, что
- $h_{\theta}(x) \geq 0,5$ и $ y = 1$, когда $ X\theta \geq 0 $, и соответственно
- $h_{\theta}(x) \ < 0,5 $ и $ y = 0$, когда $ X\theta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить это пространство на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $\theta_0$, $\theta_1$ и $\theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = \theta_0 + \theta_1 x_1 + \theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{\theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = \theta_0 + \theta_1 x_1 + \theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = \theta_0 + 0 + \theta_2 x_2 \rightarrow x_2 = -\frac{\theta_0}{\theta_2} \rightarrow c = -\frac{\theta_0}{\theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = \frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = \theta_1x_1^b + \theta_2x_2^b + \theta_0-(\theta_1x_1^a + \theta_2x_2^a + \theta_0) $$
$$ -\theta_2(x_2^b-x_2^a) = \theta_1(x_1^b-x_1^a) $$
А значит,
$$ \frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -\frac{\theta_1}{\theta_2} \rightarrow m = -\frac{\theta_1}{\theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
1 2 3 |
# возьмем большое отрицательное значение z = -999 1 / (1 + np.exp(-z)) |
|
1 2 |
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-z}} \times \frac{e^z}{e^z} = \frac{e^z}{e^z(1+e^{-z})} = \frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
1 2 |
z = 999 1 / (1 + np.exp(-z)) |
|
1 |
1.0 |
При этом вторая стабильна при очень больших отрицательных значениях.
|
1 2 |
z = -999 np.exp(z) / (np.exp(z) + 1) |
|
1 |
0.0 |
Объединим обе части с помощью условия.
|
1 2 3 4 5 |
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(-z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Можно также использовать функцию expit() библиотеки scipy.
|
1 2 |
from scipy.special import expit expit(999), expit(-999) |
|
1 |
(1.0, 0.0) |
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
1 2 3 4 |
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
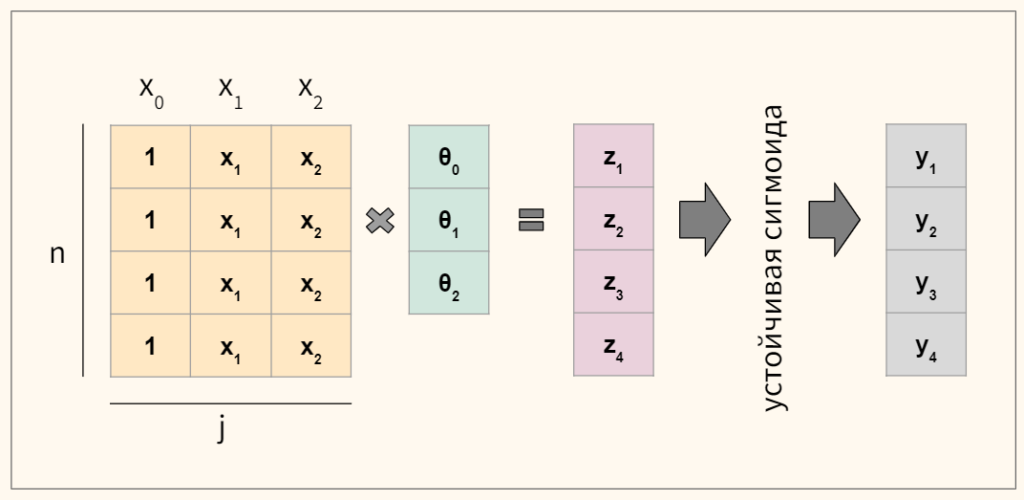
Пропишем это на Питоне.
|
1 2 3 4 5 6 7 8 |
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([-3, 1, 1]) # подадим их в модель h(x, thetas) |
|
1 |
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $\theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула функции логистической ошибки
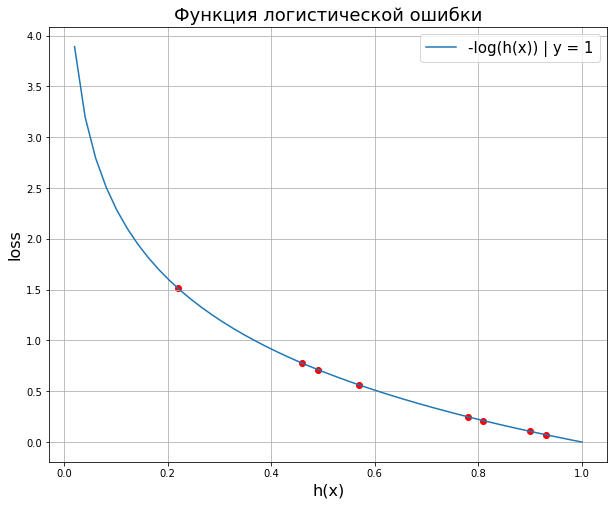
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{\theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; \theta)) = -log(h_{\theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях, близких к нулю.
$$ -log(1-P(y = 1 | x; \theta)) = -log(1-h_{\theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(\theta) = \begin{cases} -log(h_{\theta}(x)) | y=1 \\ -log(1-h_{\theta}(x)) | y=0 \end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на $y$, а правую на $1-y$. Тогда, если речь идет о классе 1, первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(\theta) = -\frac{1}{n} \sum y \cdot log(h_{\theta}(x)) + (1-y) \cdot log(1-h_{\theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
1 2 3 4 5 6 7 |
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ 'y' :[1, 1, 1, 0, 0, 1, 1, 0], 'y_pred' :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |

Найдем вероятность принадлежности к классу 1.
|
1 2 3 |
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output['y=1 prob'] = np.where(output['y'] == 0, 1 - output['y_pred'], output['y_pred']) output |

Возьмем отрицательный логарифм из каждой вероятности.
|
1 2 |
output['-log'] = -np.log(output['y=1 prob']) output |

Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, -np.log(x_vals), label = '-log(h(x)) | y = 1') # выведем каждое из значений отрицательного логарифма plt.scatter(output['y=1 prob'], output['-log'], color = 'r') # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel('h(x)', fontsize = 16) plt.ylabel('loss', fontsize = 16) plt.title('Функция логистической ошибки', fontsize = 18) plt.legend(loc = 'upper right', prop = {'size': 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
|
1 |
output['-log'].mean() |
|
1 |
0.5254048659083239 |
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
1 2 3 4 5 6 7 8 9 10 |
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e-9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 - y) * np.log(1 - y_pred + 1e-9) # сложим и разделим на количество наблюдений return -np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
1 |
objective(output['y'], output['y_pred']) |
|
1 |
0.525404864006128 |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(\theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(\theta)$,
$$ G = y \cdot log(h) + (1-y) \cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(\theta)$ — линейная функция $x\theta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ \frac{\partial G}{\partial \theta} = \frac{\partial G}{\partial h} \cdot \frac{\partial h}{\partial z} \cdot \frac{\partial z}{\partial \theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ \frac{\partial}{\partial x} ln f(x) = \frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ \frac{\partial G}{\partial h} \left[ y \cdot log(h) + (1-y) \cdot log(1-h) \right] $$
$$ = y \cdot \frac{\partial G}{\partial h} [log(h)] + (1-y) \cdot \frac{\partial G}{\partial h} [log(1-h)] $$
$$ = \frac{1}{h}y + \frac{1}{1-h} \cdot \frac{\partial G}{\partial h} [1-h] \cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = \frac{h}{y} + \frac{\frac{\partial G}{\partial h} (1-h) (1-y)}{1-h} = \frac{h}{y}+\frac{(0-1)(1-y)}{1-h} $$
$$ = \frac{y}{h}-\frac{1-y}{1-h} = \frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ \frac{\partial h}{\partial z} \left[ \frac{1}{1+e^{-z}} \right] = \frac{\partial h}{\partial z} \left[ (1+e^{-z})^{-1}) \right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) \cdot (-e^{-z}) = \frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}} = \frac{1}{1+e^{-z}} \cdot \frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = \frac{1}{1+e^{-z}} \cdot \left( \frac{1+e^{-z}}{1+e^{-z}}-\frac{1}{1+e^{-z}} \right) $$
$$ = \frac{1}{1+e^{-z}} \cdot \left( 1-\frac{1}{1+e^{-z}} \right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ \frac{\partial z}{\partial \theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ \frac{\partial J}{\partial \theta} = \frac{y-h}{h(1-h)} \cdot h(1-h) \cdot x_j \cdot \frac{1}{n} = x_j \cdot (y-h) \cdot \frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ \nabla_{\theta} J = X^T(h(X\theta)-y) \times \frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.

Объявим соответствующую функцию.
|
1 2 |
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred - y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
1 2 3 4 5 6 7 8 9 10 11 |
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df['target'] = data.target # посмотрим на первые три строки df.head(3) |

Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
1 |
df.shape, np.unique(df.target) |
|
1 |
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
1 2 3 4 5 |
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
1 |
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop('target', axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df['target'])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({'column': columns, 'correlation': correlations}).style.background_gradient() |

Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
1 2 3 4 |
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |

Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
1 2 3 4 5 6 7 8 9 |
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = 'upper left', prop = {'size': 15}) # выведем результат plt.show() |
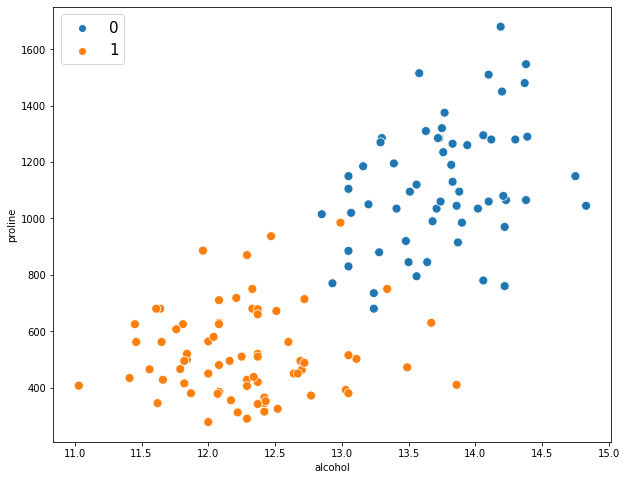
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
1 2 |
X = df[['alcohol', 'proline']] y = df['target'] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
1 2 3 |
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X - X.mean()) / X.std() X.head() |

Проверим результат.
|
1 |
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
1 |
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
1 2 3 |
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,'x0', np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
1 2 3 4 5 |
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |

Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
1 2 |
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
1 |
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
|
1 |
loss_history = [] |
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
1 2 3 4 5 6 7 8 9 10 11 |
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas - 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
1 2 3 |
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[-1] |
|
1 |
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
1 2 3 4 5 6 7 8 9 |
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 - отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
1 2 3 4 5 |
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
1 |
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность, близкая к нулю, говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
1 2 |
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
1 |
0.9615384615384616 |
|
1 2 3 4 5 6 |
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками - фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1'], index = ['Actual 0', 'Actual 1']) |

Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
1 2 3 |
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = -thetas[0]/thetas[2], -thetas[1]/thetas[2] c, m |
|
1 |
(0.1227046263531282, -0.915731474695505) |
|
1 2 3 4 5 6 7 8 |
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X['alcohol']), max(X['alcohol']) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X['proline']), max(X['proline']) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
1 |
array([-2.15362589, 2.12194856]) |
|
1 2 3 4 5 |
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
1 2 |
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, 'k', lw = 1, ls = '--') # дополнительно отобразим наши данные, sns.scatterplot(x = X['alcohol'], y = X['proline'], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = 'upper left', prop = {'size': 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color='tab:blue', alpha = 0.2) # plt.fill_between(xd, yd, ymax, color='tab:orange', alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel('x_1') # plt.ylabel('x_2') plt.show() |

На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст "правильные" копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст "правильную" копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее def add_ones(self, x): return x.insert(0,'x0', np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e-9) y_zero_loss = (1 - y) * np.log(1 - y_pred + 1e-9) return -np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred - y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(-z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[['alcohol', 'proline']] y = df['target'] # приведем признаки к одному масштабу X = (X - X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[-1] |
|
1 |
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
1 2 3 4 5 |
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
1 |
(0, 0.022908352078195617) |
|
1 2 |
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
1 |
0.9615384615384616 |
|
1 2 3 4 |
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1'], index = ['Actual 0', 'Actual 1']) |

Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# подготовим данные X = df[['alcohol', 'proline']] y = df['target'] X = (X - X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
1 |
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствующие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
1 2 3 4 5 6 7 8 |
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
1 |
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
1 |
accuracy_score(y, y_pred) |
|
1 |
0.9615384615384616 |
И построим матрицу ошибок.
|
1 2 3 |
pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1'], index = ['Actual 0', 'Actual 1']) |

Как мы видим, хотя веса модели и предсказанные вероятности немного отличаются, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
1 2 3 |
# найдем сдвиг и наклон для уравнения решающей границы c, m = -model.intercept_ / model.coef_[0][1], -model.coef_[0][0] / model.coef_[0][1] c, m |
|
1 |
(array([0.12536569]), -0.8521526076691505) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X['alcohol']), max(X['alcohol']) ymin, ymax = min(X['proline']), max(X['proline']) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, 'k', lw=1, ls='--') sns.scatterplot(x = X['alcohol'], y = X['proline'], hue = y, s = 70) plt.legend(loc = 'upper left', prop = {'size': 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |

Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.

Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = \theta_{0}x_0 + \theta_{1}x_1 + \theta_{2}x_2 + \theta_{3} x_1^2 + \theta_{4} x_1x_2 + \theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим, улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
1 2 3 4 |
X = df[['alcohol', 'proline']] y = df['target'] X = (X - X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
1 2 3 4 5 6 |
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
1 2 |
# посмотрим на первое наблюдение X.head(1) |

|
1 2 |
# должно получиться шесть признаков X_poly[:1] |
|
1 2 |
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
1 2 3 4 5 6 7 8 9 10 11 |
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
|
1 |
0.9615384615384616 |
Построим матрицу ошибок.
|
1 2 3 |
pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1'], index = ['Actual 0', 'Actual 1']) |

Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
1 2 3 4 5 6 7 8 |
# сделаем копию исходного датафрейма с нужными признаками predictions = df[['alcohol', 'proline']].copy() # и добавим новый столбец с прогнозными значениями predictions['y_pred'] = y_pred # посмотрим на результат predictions.head(3) |
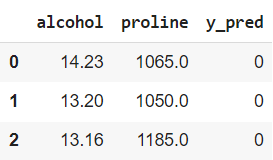
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {'wspace' : 0.2}) # на левом подграфике выведем фактические классы sns.scatterplot(data = df, x = 'alcohol', y = 'proline', hue = 'target', palette = 'bright', s = 50, ax = ax1) ax1.set_title('Фактические классы', fontsize = 14) # на правом - прогнозные sns.scatterplot(data = predictions, x = 'alcohol', y = 'proline', hue = 'y_pred', palette = 'bright', s = 50, ax = ax2) ax2.set_title('Прогноз', fontsize = 14) # зададим общий заголовок fig.suptitle('Бинарная полиномиальная регрессия', fontsize = 16) plt.show() |
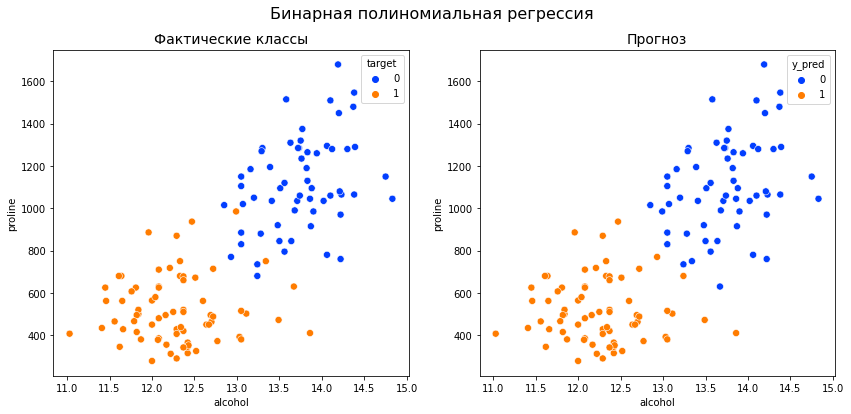
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df - df.mean())/df.std() # добавим целевую переменную df['target'] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 2 3 4 |
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() - values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() - values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop('target', axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df['target'])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({'column': columns, 'correlation': correlations}).style.background_gradient() |

Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
1 2 |
df = df[['flavanoids', 'proline', 'target']].copy() df.head(3) |
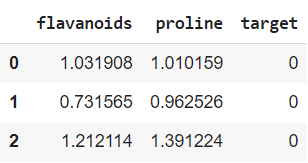
Посмотрим, насколько легко можно разделить эти классы.
|
1 2 3 4 5 6 7 |
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = 'bright', s = 100) # добавим легенду plt.legend(loc = 'upper left', prop = {'size': 15}) plt.show() |

Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
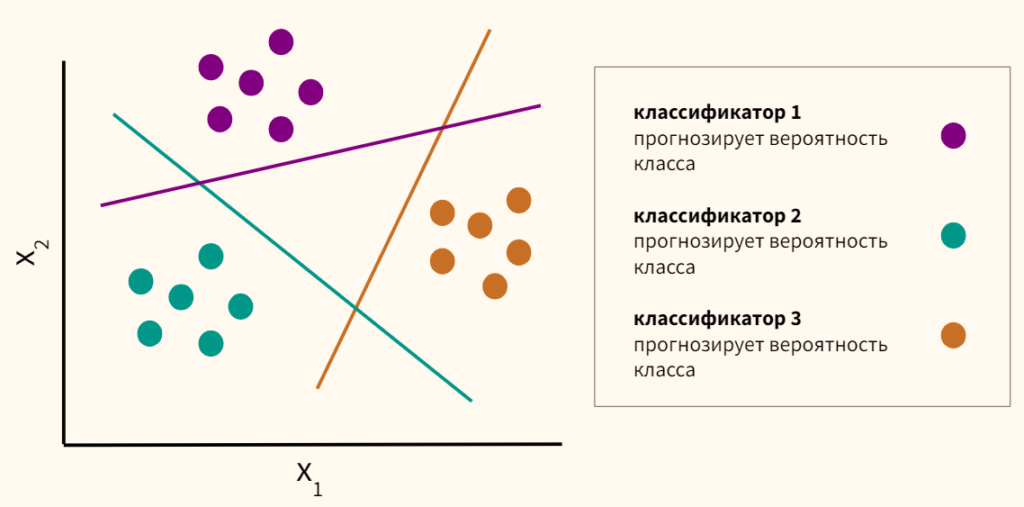
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_\theta^{(i)}(x) = P(y = i | x; theta), i \in \{0, 1, 2\} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
1 2 3 4 5 |
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 |
array([0, 1, 2]) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 первым классом будет класс 0, а классы 1 и 2 - нулевым ovr_0['target'] = np.where(df['target'] == target[0], 1, 0) ovr_1['target'] = np.where(df['target'] == target[1], 1, 0) ovr_2['target'] = np.where(df['target'] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {'wspace': 0.2, 'hspace': 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = 'target', s = 50, ax = ax1) ax1.set_title('Прогнозирование класса 0', fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = 'target', s = 50, ax = ax2) ax2.set_title('Прогнозирование класса 1', fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = 'target', s = 50, ax = ax3) ax3.set_title('Прогнозирование класса 2', fontsize = 14) plt.show() |

Обучение моделей
|
1 2 3 4 5 6 7 8 9 10 11 12 |
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[['flavanoids', 'proline']] y = ova_n['target'] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
1 2 3 |
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
1 |
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
1 2 3 4 5 6 7 8 9 10 11 |
# вновь перенесем данные из исходного датафрейма X = df[['flavanoids', 'proline']] y = df['target'] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
1 2 3 |
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
1 |
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
1 2 3 4 |
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), -1).T all_probs.shape |
|
1 2 3 |
# каждая из 178 строк - это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
1 |
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу.
|
1 2 |
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
1 |
|
1 2 3 4 5 6 |
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
1 |
0.9157303370786517 |
|
1 2 3 4 |
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1', 'Forecast 2'], index = ['Actual 0', 'Actual 1', 'Actual 2']) |

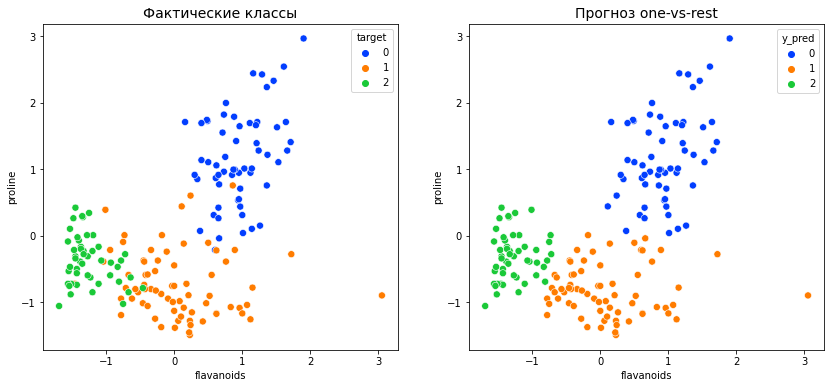
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
predictions = df[['flavanoids', 'proline']].copy() predictions['y_pred'] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {'wspace': 0.2, 'hspace': 0.08}) sns.scatterplot(data = df, x = 'flavanoids', y = 'proline', hue = 'target', palette = 'bright', s = 50, ax = ax1) ax1.set_title('Фактические классы', fontsize = 14) sns.scatterplot(data = predictions, x = 'flavanoids', y = 'proline', hue = 'y_pred', palette = 'bright', s = 50, ax = ax2) ax2.set_title('Прогноз one-vs-rest', fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop('target', axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), -1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x['target'] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop('target', axis = 1).copy() ovr_df['target'] = np.where(x['target'] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,'x0', np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e-9) y_zero_loss = (1 - y) * np.log(1 - y_pred + 1e-9) return -np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred - y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(-z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
1 2 3 4 5 6 7 8 |
X = df[['flavanoids', 'proline']] y = df['target'] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
|
1 |
0.9157303370786517 |
Сравнение с sklearn
Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
1 2 3 4 5 6 7 8 |
X = df[['flavanoids', 'proline']] y = df['target'] ovr_model = LogisticRegression(multi_class = 'ovr') ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
|
1 |
0.898876404494382 |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
X = df[['flavanoids', 'proline']] y = df['target'] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = 'ovr') poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
|
1 |
0.9157303370786517 |
Результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
predictions = df[['flavanoids', 'proline']].copy() predictions['y_pred'] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {'wspace': 0.2, 'hspace': 0.08}) sns.scatterplot(data = df, x = 'flavanoids', y = 'proline', hue = 'target', palette = 'bright', s = 50, ax = ax1) ax1.set_title('Фактические классы', fontsize = 14) sns.scatterplot(data = predictions, x = 'flavanoids', y = 'proline', hue = 'y_pred', palette = 'bright', s = 50, ax = ax2) ax2.set_title('Полиномиальная регрессия', fontsize = 14) plt.show() |

Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные на несколько датасетов и использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
1 2 3 |
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,'x0', np.ones(x.shape[0])) |
|
1 2 3 4 |
X = df[['flavanoids', 'proline']] add_ones(X) X.head(3) |

Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
1 2 3 4 5 6 7 8 9 10 |
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
1 2 3 4 |
y = df['target'] y_enc = ohe(df['target']) y_enc[:3] |
|
1 2 3 |
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
1 2 3 |
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
1 |
array([0, 1, 2]) |
|
1 2 |
y_lb = lb.transform(y) y_lb[:5] |
|
1 2 3 4 5 |
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $\theta_0$) и трех классов.

Инициализируем веса.
|
1 2 |
thetas = np.zeros((3, 3)) thetas |
|
1 2 3 |
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ \text{softmax}(z)_{i} = \frac{e^{z_i}}{\sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-X\theta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
|
1 |
X.shape, thetas.shape |
|
1 |
((178, 3), (3, 3)) |
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
1 2 |
z = np.dot(-X, thetas) z.shape |
|
1 |
(178, 3) |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
1 |
z[:5] |
|
1 2 3 4 5 |
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ \text{softmax}(z)_{i} = \frac{e^{z_i-max(z)}}{\sum_{k=1}^N e^{z_k-max(z)}} $$
|
1 2 3 |
# axis = -1 - это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = -1, keepdims = True)[:5] |
|
1 2 3 4 5 |
array([[0.], [0.], [0.], [0.], [0.]]) |
|
1 2 |
z = z - np.max(z, axis = -1, keepdims = True) z[:5] |
|
1 2 3 4 5 |
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
1 2 |
arr = np.array([-2, 3, 0, -7, 6]) arr - max(arr) |
|
1 |
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
1 2 |
numerator = np.exp(z) numerator[:5] |
|
1 2 3 4 5 |
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
1 2 |
denominator = np.sum(numerator, axis = -1, keepdims = True) denominator[:5] |
|
1 2 3 4 5 |
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
1 2 |
softmax = numerator / denominator softmax[:5] |
|
1 2 3 4 5 |
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $\theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
1 2 3 4 5 6 7 |
def stable_softmax(x, thetas): z = np.dot(-x, thetas) z = z - np.max(z, axis = -1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = -1, keepdims = True) softmax = numerator / denominator return softmax |
|
1 2 |
probs = stable_softmax(X, thetas) probs[:3] |
|
1 2 3 |
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = \frac{e^{z_1}}{e^{z_1}+e^0} = \frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = \frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмоиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, \theta) = -\frac{1}{n} \sum y \cdot log(h_{\theta}(x)) + (1-y) \cdot log(1-h_{\theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -\sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности наблюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде переключателя. Здесь при умножении «срабатывает» только первая вероятность $1 \times 0,3 + 0 \times 0,4 + 0 \times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна).
|
1 2 3 4 |
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) -np.sum(y_ohe * np.log(softmax)) |
|
1 |
1.2039728043259361 |
Если бы модель в своих вероятностях ошибалась меньше, то и общая ошибка была бы меньше.
|
1 2 3 4 |
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) -np.sum(y_ohe * np.log(softmax)) |
|
1 |
0.916290731874155 |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
1 2 3 4 5 |
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=-np.log(x_arr)) plt.title('Plot of -log(x)') plt.xlabel('x') plt.ylabel('-log(x)'); |

Напишем функцию.
|
1 2 3 4 5 |
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e-9): n = probs.shape[0] ce = -np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
1 2 |
ce = cross_entropy(probs, y_enc) ce |
|
1 |
1.0986122856681098 |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ \nabla_{\theta}J = \frac{1}{n} \times X^T \cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
1 2 3 |
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc - probs))) |
|
1 |
gradient_softmax(X, probs, y_enc) |
|
1 2 3 |
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e-9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas - 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $\theta_0$)) и достигнутый уровень ошибки.
|
1 |
thetas |
|
1 2 3 |
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
1 |
loss_history[0], loss_history[-1] |
|
1 |
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
1 |
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
1 |
accuracy_score(y, y_pred) |
|
1 |
0.9044943820224719 |
|
1 2 3 |
pd.DataFrame(confusion_matrix(y, y_pred), columns = ['Forecast 0', 'Forecast 1', 'Forecast 2'], index = ['Actual 0', 'Actual 1', 'Actual 2']) |

Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e-9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas - 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(-x, thetas) z = z - np.max(z, axis = -1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = -1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e-9): n = probs.shape[0] ce = -np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc - probs))) def add_ones(self, x): return x.insert(0,'x0', np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
1 2 3 4 5 6 7 |
X = df[['flavanoids', 'proline']] y = df['target'] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[-1] |
|
1 2 3 |
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
1 2 3 |
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
|
1 |
0.9044943820224719 |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
1 2 3 4 5 6 7 8 9 10 11 |
X = df[['flavanoids', 'proline']] y = df['target'] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = 'multinomial') # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
1 2 3 4 |
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
1 2 3 |
y_pred = model.predict(X) accuracy_score(y, y_pred) |
|
1 |
0.898876404494382 |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию логистической регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.

Рассмотрим обучение нейронных сетей.