Все курсы > Анализ и обработка данных > Занятие 4 (часть 2)
Во второй части занятия рассмотрим нахождение различий в данных и выявление взаимосвязи.
Продолжим работать в том же ноутбуке⧉
Нахождение различий

Два категориальных признака
Вначале возьмем случай двух категориальных признаков. Например, мы хотим понять насколько выживаемость пассажира (целевая переменная) зависит от класса, которым он путешествовал.
countplot и barplot
В первую очередь стоит визуально оценить, есть ли такое различие или нет. Для этого подойдут столбчатые диаграммы, где мы либо располагаем два столбца целевого признака рядом друг с другом (grouped), либо делаем один столбец и разбиваем его на две части (stacked).
Библиотека Seaborn
Начнем с того, что построим несколько counplots/barplots в библиотеке Seaborn с помощью функции countplot() и параметра hue.
|
1 2 3 |
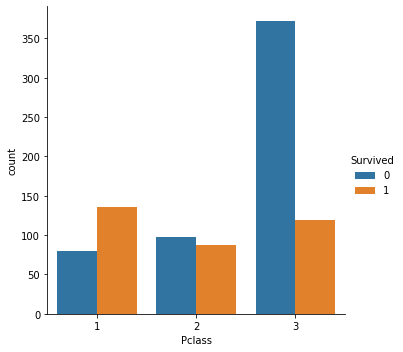
# создадим grouped countplot, где по оси x будет класс, а по оси y - количество пассажиров # в каждом классе данные разделены на погибших (0) и выживших (1) sns.countplot(x = 'Pclass', hue = 'Survived', data = titanic); |

|
1 2 3 |
# горизонтальный countplot получится, # если передать данные о классе пассажира в переменную y sns.countplot(y = 'Pclass', hue = 'Survived', data = titanic); |

Для создания таких графиков мы также можем использовать более универсальную функцию catplot(). Передадим ей все те же параметры, что и функции countplot(), а также параметр kind = ‘count’, который и сообщит, что мы хотим построить именно countplot.
|
1 |
sns.catplot(x = 'Pclass', hue = 'Survived', data = titanic, kind = 'count'); |
|
1 2 |
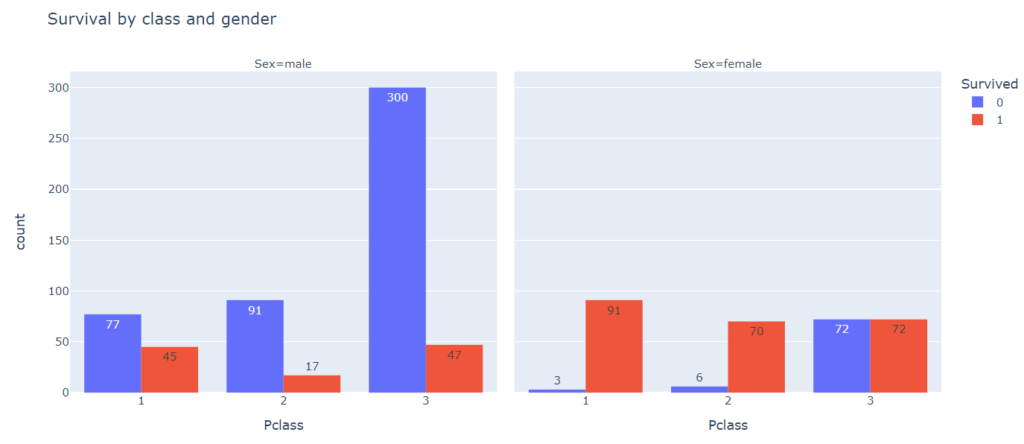
# добавим еще один признак (пол) через параметр col sns.catplot(x = 'Pclass', hue = 'Survived', col = 'Sex', kind = 'count', data = titanic); |

На основе графиков выше видно, что класс пассажира имеет большое значение для определения его виживаемости. При этом пол также оказал влияние. Например, в третьем классе большая часть мужчин погибла, в то время как среди женщин, количество выживших и не выживших примерно одинаковое.
Теперь посмотрим, как создать подобные графики в библиотеке Plotly.
Библиотека Plotly
Для построения графика countplot используем функцию px.histogram() (для barplot подойдет px.bar()). Начнем с варианта, когда разбитые по какому-либо признаку столбцы стоят рядом друг с другом (grouped).
|
1 2 3 4 5 6 7 |
px.histogram(titanic, # возьмем данные x = 'Pclass', # диаграмму будем строить по столбцу Pclass color = 'Survived', # с разбивкой на выживших и погибших barmode = 'group', # разделенные столбцы располагаются рядом друг с другом text_auto = True, # выведем количество наблюдений в каждом столбце title = 'Survival by class' # также добавим заголовок ) |

Теперь выведем вариант, когда каждый столбец диаграммы разделен на две части (stacked). Так как мы будем вручную корректировать подписи к графику и расстояние между столбцами, необходимо использовать объектно-ориентированный подход.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# создадим объект fig, в который поместим столбчатую диаграмму fig = px.histogram(titanic, x = 'Pclass', color = 'Survived', barmode = 'stack', # каждый столбец класса будет разделен по признаку Survived text_auto = True) # применим метод .update_layout к объекту fig fig.update_layout( title_text = 'Survival by class', # заголовок xaxis_title_text = 'Pclass', # подпись к оси x yaxis_title_text = 'Count', # подпись к оси y bargap = 0.2, # расстояние между столбцами # подписи классов пассажиров на оси x xaxis = dict( tickmode = 'array', tickvals = [1, 2, 3], ticktext = ['Class 1', 'Class 2', 'Class 3'] ) ) fig.show() |

Теперь разобьем данные по трем категориальным переменным: полу, классу и выживаемости.
|
1 2 3 4 5 6 7 8 |
# для этого используем новый параметр facet_col = 'Sex' px.histogram(titanic, x = 'Pclass', color = 'Survived', facet_col = 'Sex', barmode = 'group', text_auto = True, title = 'Survival by class and gender') |
Более того, мы можем добавить еще один категориальный признак, порт посадки пассажира (Embarked).
|
1 2 3 4 5 6 7 8 9 |
# используем одновременно параметры facet_col и facet_row px.histogram(titanic, x = 'Pclass', color = 'Survived', facet_col = 'Embarked', facet_row = 'Sex', barmode = 'group', text_auto = True, title = 'Survival by class, gender and port of embarkation') |
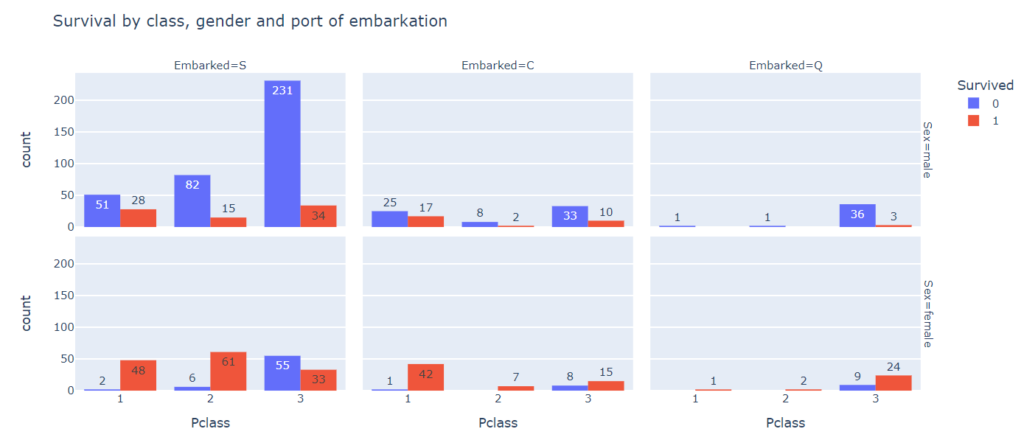
Здесь конечно, нужно следить за тем, чтобы объем предоставляемой информации не ухудшал информативности графиков.
Таблица сопряженности
Таблица сопряженности (contingency table) позволяет количественно измерить зависимость одной категориальной переменной от другой. Например, количественно оценим зависимость выживаемости от класса пассажира. Вначале оценим абсолютное количество наблюдений.
Абсолютное количество наблюдений
Для создания таблиц сопряженности в библиотеке Pandas используется функция pd.crosstab().
|
1 2 3 4 5 6 7 8 9 10 |
# создадим таблицу сопряженности # в параметр index мы передадим данные по классу, в columns - по выживаемости pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived) # создадим названия категорий класса и выживаемости pclass_abs.index = ['Class 1', 'Class 2', 'Class 3'] pclass_abs.columns = ['Not survived', 'Survived'] # выведем результат pclass_abs |

Теперь для каждого класса мы видим количество выживших и количество погибших. На основе таблицы сопряженности очень удобно строить столбчатую диаграмму (можно использовать график barplot, а не countplot, потому что количество значений в каждой категории уже посчитано).
Начнем с библиотеки Pandas.
|
1 2 3 |
# построим grouped barplot в библиотеке Pandas # rot = 0 делает подписи оси х вертикальными pclass_abs.plot.bar(rot = 0); |

|
1 2 |
# параметр stacked = True делит каждый столбец класса на выживших и погибших pclass_abs.plot.bar(rot = 0, stacked = True); |
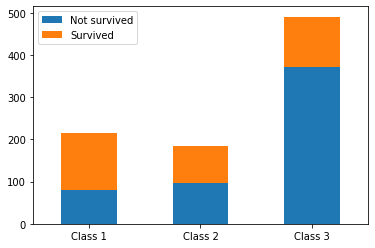
Теперь посмотрим, как построить stacked barplot в библиотеке Matplotlib.
|
1 2 3 4 |
# вначале создадим barplot для одной (нижней) категории plt.bar(pclass_abs.index, pclass_abs['Not survived']) # затем еще один barplot для второй (верхней), указав нижнуюю в параметре bottom plt.bar(pclass_abs.index, pclass_abs['Survived'], bottom = pclass_abs['Not survived']); |
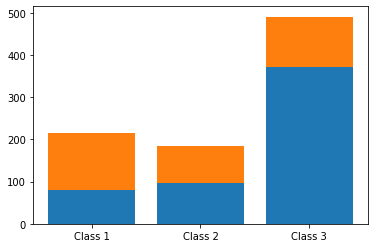
Таблица сопряженности вместе с суммой
С помощью параметра margins = True мы можем вывести сумму наблюдений по каждой строке и каждому столбцу (эти показатели еще называют маргинальными частотами, marginal frequencies).
|
1 2 3 4 5 6 7 8 9 |
# для подсчета суммы по строкам и столбцам используется параметр margins = True pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, margins = True) # новой строке и новому столбцу с суммами необходимо дать название (например, Total) pclass_abs.index = ['Class 1', 'Class 2', 'Class 3', 'Total'] pclass_abs.columns = ['Not survived', 'Survived', 'Total'] pclass_abs |
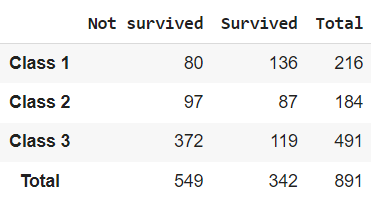
Относительное количество наблюдений
Для получения относительного количества наблюдений (относительных частот) следует использовать параметр normalize. Так как нам важно понимать долю выживших и долю погибших, укажем normalize = 'index'. В этом случае каждое значение будет разделено на общее количество наблюдений в строке.
|
1 2 3 4 5 6 7 8 |
# сумма по строкам в этом случае должна быть равна единице pclass_rel = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, normalize = 'index') pclass_rel.index = ['Class 1', 'Class 2', 'Class 3'] pclass_rel.columns = ['Not survived', 'Survived'] pclass_rel |

Если бы в индексе (в строках) была выживаемость, а в столбцах — классы, то логично было бы использовать параметр normalize = 'columns' для деления на сумму по столбцам.
|
1 2 3 4 5 6 7 |
pclass_rel_T = pd.crosstab(index = titanic.Survived, columns = titanic.Pclass, normalize = 'columns') pclass_rel_T.index = ['Not survived', 'Survived'] pclass_rel_T.columns = ['Class 1', 'Class 2', 'Class 3'] pclass_rel_T |

Теперь на stacked barplot мы видим доли выживших в каждом из классов.
|
1 |
pclass_rel.plot.bar(rot = 0, stacked = True).legend(loc = 'lower left'); |

Количественный и категориальный признаки
rcParams
Прежде чем продолжить, давайте посмотрим, как мы можем задать размер для всех (или почти всех) последующих графиков в ноутбуке. Так нам не придется вручную менять размер каждой визуализации.
В библиотеке Matplotlib и связанных с ней библиотеках (например, Seaborn) есть так называемые параметры конфигурации среды (runtime configuration parameters), то есть параметры, которые используются по умолчанию при создании графиков.
Эти параметры и их значения содержатся в словаре, к которому можно получить доступ через атрибут rcParams библиотеки Matplotlib.
|
1 2 3 4 5 |
# импортируем всю библиотеку Matplotlib import matplotlib # и посмотрим, какой размер графиков (ключ figure.figsize) установлен по умолчанию matplotlib.rcParams['figure.figsize'] |
|
1 |
[6.0, 4.0] |
Изменить эти параметры можно, обновив значение словаря rcParams по соответствующему ключу. Передадим новое значение размера по ключу figure.figuresize.
|
1 2 3 |
# обновим этот параметр через прямое внесение изменений в значение словаря matplotlib.rcParams['figure.figsize'] = (7, 5) matplotlib.rcParams['figure.figsize'] |
|
1 |
[7.0, 5.0] |
Также можно воспользоваться функцией sns.set() или, что то же самое, sns.set_theme().
|
1 2 3 4 5 |
# изменим размер обновив словарь в параметре rc функции sns.set() sns.set(rc = {'figure.figsize' : (8, 5)}) # посмотрим на результат matplotlib.rcParams['figure.figsize'] |
|
1 |
[8.0, 5.0] |
Теперь все последующие графики в библиотеках Matplotlib, Seaborn и Pandas будут иметь размеры восемь на пять дюймов. Вернемся к исследованию переменных.
Гистограммы
Когда у нас есть одна количественная и одна категориальная переменные, для их визуализации проще всего построить две наложенные друг на друга гистограммы. Мы уже строили такие графики в рамках вводного курса.
Посмотрим, различается ли распределение возраста выживших и погибших пассажиров Титаника.
|
1 2 3 4 |
# выведем две гистограммы на одном графике в библиотеке Matplotlib # отфильтруем данные по погибшим и выжившим и построим гистограммы по столбцу Age plt.hist(x = titanic[titanic['Survived'] == 0]['Age']) plt.hist(x = titanic[titanic['Survived'] == 1]['Age']); |
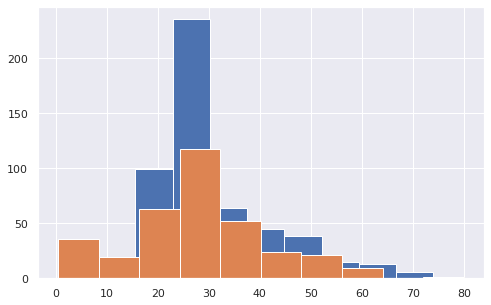
Теперь посмотрим, зависит ли распределение возраста от пола пассажира.
|
1 2 |
# в библиотеке Seaborn в x мы поместим количественный признак, в hue - категориальный sns.histplot(x = 'Age', hue = 'Sex', data = titanic, bins = 10); |

|
1 2 |
# в Plotly количественный признак помещается в x, категориальный - в color px.histogram(titanic, x = 'Age', color = 'Sex', nbins = 8, text_auto = True) |
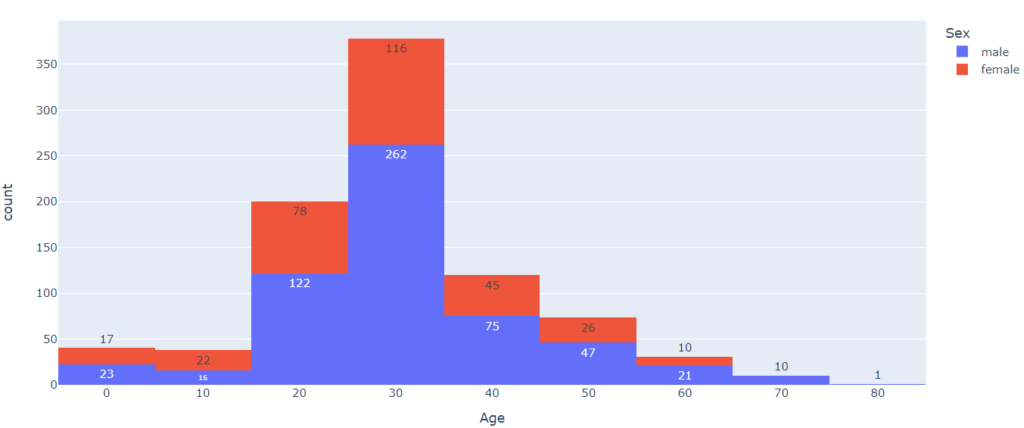
Сравнение двух распределений может быть не вполне корректным, если размер выборок существенно различается. Например, в нашем случае количество мужчин и женщин на борту далеко не одинаково.
|
1 2 |
# сравним количество мужчин и женщин на борту titanic.Sex.value_counts() |
|
1 2 3 |
male 577 female 314 Name: Sex, dtype: int64 |
Исправить ситуацию может параметр density = True.
|
1 2 3 |
# параметр alpha отвечает за прозрачность каждой из гистограмм plt.hist(x = titanic[titanic['Sex'] == 'male']['Age'], density = True, alpha = 0.5) plt.hist(x = titanic[titanic['Sex'] == 'female']['Age'], density = True, alpha = 0.5); |
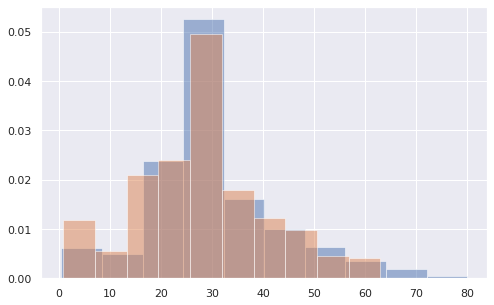
В этом случае гистограмма показывает плотность вероятности, а ее общая площадь всегда равна единице. Как следствие, мы можем адекватно сравнивать распределения между собой.
График плотности
С другой стороны, для плотности вероятности есть отдельный график, density plot. Площадь под кривой такого графика также всегда равна единице. Воспользуемся функцией .displot() с параметром kde = True.
|
1 2 |
# построим графики плотности распределений суммы чека в обеденное и вечернее время sns.displot(tips, x = 'total_bill', hue = 'time', kind = 'kde'); |
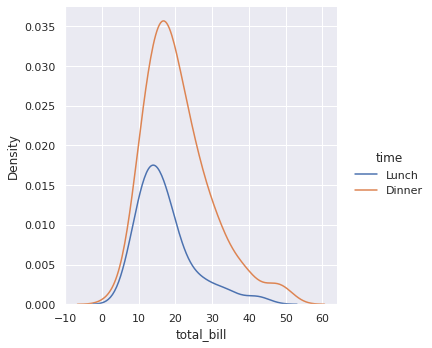
Из-за особенностей расчета графика kde мы можем получить «неестественные значения». Например, на диаграмме выше встречаются отрицательные значения чека. В реальности такого быть не может.
Избавиться от таких значений можно с помощью параметра clip, который задает диапазон значений.
|
1 2 3 |
# зададим границы диапазона от 0 до 70 долларов через clip = (0, 70) # дополнительно заполним цветом пространство под кривой с помощью fill = True sns.displot(tips, x = 'total_bill', hue = 'time', kind = 'kde', clip = (0, 70), fill = True); |

boxplots
Для сравнения распределений количественной переменной, разбитой по какому-либо категориальному признаку, также очень удобно использовать несколько графиков boxplot (side-by-side boxplots).
Построим такие графики в библиотеках Seaborn и Plotly. Вначале посмотрим, как различается сумма чека по дням недели.
|
1 |
sns.boxplot(x = 'day', y = 'total_bill', data = tips); |
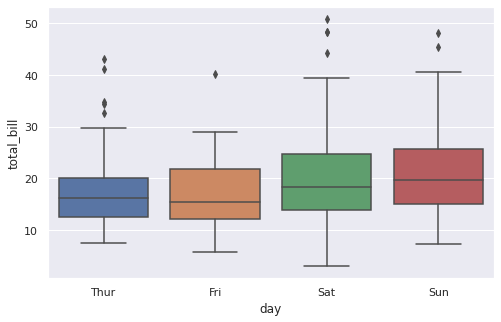
Что можно сказать про эти распределения?
- Медианный чек выше по воскресеньям
- Самый широкий диапазон суммы по чеку наблюдается в субботу, в пятницу же наоборот разброс наименьший
- Выбросы присутствуют только в верхних значениях распределения
Теперь посмотрим, как различается сумма чека в обеденное и вечернее время.
|
1 |
px.box(tips, x = 'time', y = 'total_bill', points = 'all') |
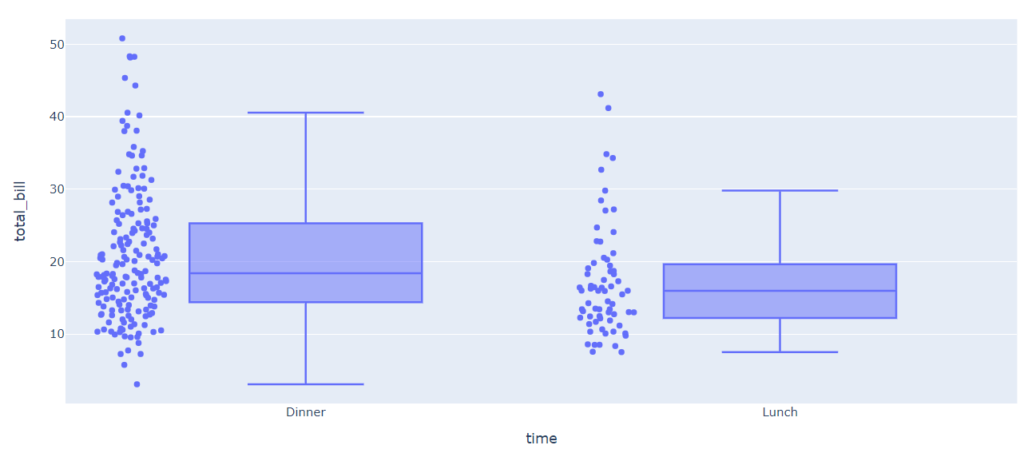
Ожидаемо, как разброс, так и медианное значение меньше в обеденное время.
Дополнительно замечу, что с помощью параметра points = ‘all’ в библиотеке Plotly для каждого распределения мы построили график, который называется stripplot. Он, в частности, показывает, что гостей за ужином бывает существенно больше. Об этом графике мы дополнительно поговорим чуть ниже.
Гистограммы и boxplots
Гистограммы и boxplots можно совместить. Сделать это проще всего в Plotly.
|
1 2 3 4 |
px.histogram(tips, x = 'total_bill', # количественный признак color = 'sex', # категориальный признак marginal = 'box') # дополнительный график: boxplot |
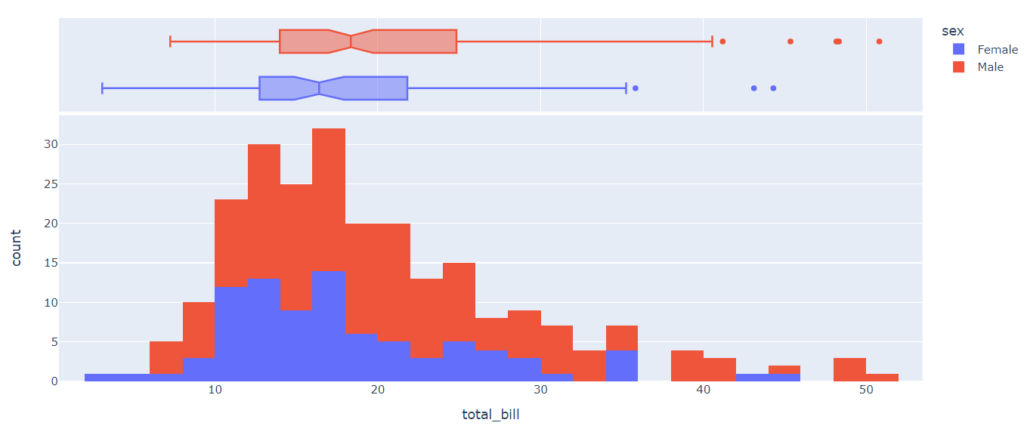
stripplot, violinplot
Более редкими типами графиков для визуализации количественных распределений являются stripplot и violinplot. Первый график, stripplot, как мы уже видели выше, визуализирует сами наблюдения.
|
1 2 3 |
# по сути, stripplot - это точечная диаграмма (scatterplot), # в которой одна из переменных категориальная sns.stripplot(x = 'day', y = 'total_bill', data = tips); |
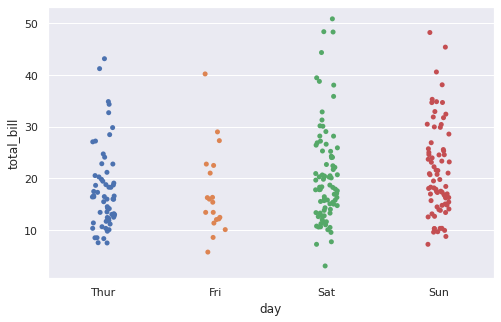
График stripplot можно построить как с помощью приведенной в примере выше функции sns.stripplot(), так и с помощью функции sns.catplot() с параметром kind = ‘strip’.
|
1 2 3 |
# с помощью sns.catplot() мы можем вывести распределение количественной переменной (total_bill) # в разрезе трех качественных: статуса курильщика, пола и времени приема пищи sns.catplot(x = 'sex', y = 'total_bill', hue = 'smoker', col = 'time', data = tips, kind = 'strip'); |

Хотя stripplot достаточно информативен сам по себе, его очень удобно применять совместно с boxplot (как мы это делали выше).
График violinplot (от англ. violin, «скрипка») представляет собой комбинацию boxplot и графика плотности.
|
1 2 |
# построим violinplot для визуализации распределения суммы чека по дням недели sns.violinplot(x = 'day', y = 'total_bill', data = tips); |

Внутри каждого из violinplot находится миниатюрный boxplot, который помогает более точно оценить параметры распределения.
Преобразования данных
Иногда так бывает, что для повышения читаемости графика, данные сначала нужно преобразовать.
Логарифмическая шкала
Например, возьмем вот такие данные о продажах.
|
1 2 |
products = ['Phone', 'TV', 'Laptop', 'Desktop', 'Tablet'] sales = [800, 4, 550, 500, 3] |
Предположим, что в этих данных нет ошибки и было действительно продано четыре телевизора и три планшета. На графике эти позиции из-за сильно различающегося масштаба будут нулевыми.
|
1 2 |
sns.barplot(x = products, y = sales) plt.title('Продажи в январе 2020 года'); |
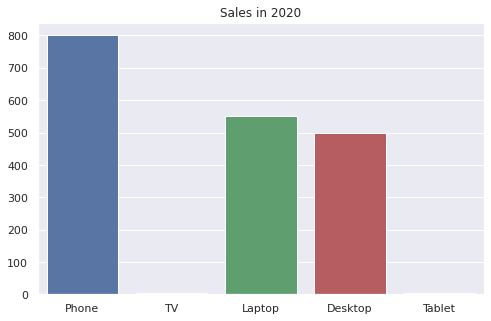
Для того чтобы эти продажи все-таки были видны, можно перевести ось y в логарифмическую шкалу.
|
1 2 3 |
sns.barplot(x = products, y = sales) plt.title('Продажи в январе 2020 года (log)') plt.yscale('log'); |

Границы по оси y
В ноутбуке с моделью текучести кадров сотрудников⧉, один из признаков — это баллы на последней аттестации. Для покинувших и продолжающих работать сотрудников различие не велико.
|
1 2 3 4 5 6 7 |
# код для получения этих значений вы найдете в ноутбуке по ссылке выше eval_left = [0.715473, 0.718113] # построим столбчатую диаграмму, # для оси x - выведем строковые категории, для y - доли покинувших компанию сотрудников sns.barplot(x = ['0', '1'], y = eval_left) plt.title('Last evaluation vs. left'); |

Иногда для наглядности бывает полезно ограничить диапазон значений по оси y.
|
1 2 3 4 5 |
sns.barplot(x = ['0', '1'], y = eval_left) plt.title('Last evaluation vs. left') # для ограничения значений по оси y можно использовать функцию plt.ylim() plt.ylim(0.7, 0.73); |

Перейдем к выявлению взаимосвязи между переменными.
Выявление взаимосвязи

Выявление взаимосвязи предполагает анализ двух количественных переменных.
На сегодняшем занятии мы поговорим про графические способы ее выявления, а в следующем разделе разберем количественные показатели взаимосвязи переменных (то есть ковариацию и корреляцию).
Линейный график
Базовым способом визуализации двух количественных переменных является линейный график (linear plot). Построить его можно с помощью функции plt.plot() библиотеки Matplotlib.
|
1 2 3 4 5 6 7 8 |
# создадим последовательность от -2пи до 2пи # с интервалом 0,1 x = np.arange(-2*np.pi, 2*np.pi, 0.1) # сделаем эту последовательность значениями по оси x, # а по оси y выведем функцию косинуса plt.plot(x, np.cos(x)) plt.title('cos(x)'); |

Точечная диаграмма
Еще один базовый график — уже знакомая нам точечная диаграмма (scatter plot). Ее удобно использовать, когда одна переменная не имеет строгой зависимости от другой. Воспользуемся функцией plt.scatter() библиотеки Matplotlib.
|
1 2 3 4 |
plt.scatter(tips.total_bill, tips.tip) plt.xlabel('total_bill') plt.ylabel('tip') plt.title('total_bill vs. tip'); |

Такой же график можно построить в библиотеке Pandas.
|
1 2 3 4 5 6 7 8 9 |
# перед созданием этого графика в Pandas принудительно удалим # предупреждения и сообщения об ошибках # (в Colab появляется предупреждение, связанное с параметром c (color)) from matplotlib.axes._axes import _log as matplotlib_axes_logger matplotlib_axes_logger.setLevel('ERROR') # воспользуемся методом .plot.scatter() tips.plot.scatter('total_bill','tip') plt.title('total_bill vs. tip'); |
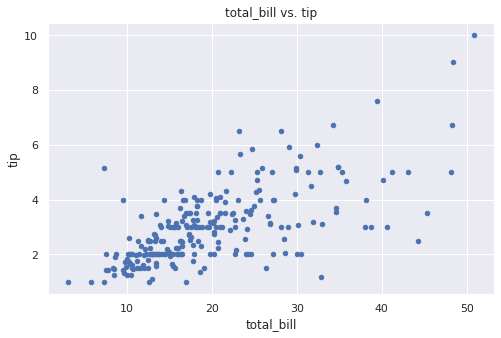
На графиках выше мы видим, что в среднем с ростом суммы чека растет и размер чаевых (другими словами, взаимосвязь прослеживается).
При этом мы видим гетероскедастичность (различную изменчивость) данных, когда при небольшом чеке диапазон чаевых меньше, чем когда сумма чека увеличивается.
Почему это влияет на качество модели и как с этим бороться, мы поговорим на следующем курсе.
В точечной диаграмме можно учесть и категориальный признак. Например, посмотрим, есть ли различие во взаимосвязи между суммой чека и размером чаевых в зависимости от времени дня.
|
1 2 3 |
# категориальный признак добавляется через параметр hue sns.scatterplot(data = tips, x = 'total_bill', y = 'tip', hue = 'time') plt.title('total_bill vs. tip by time'); |

Мы можем констатировать, что при сохранении взаимосвязи как в обеденное, так и в вечернее время, за ужином минимальная и максимальное сумма чека, а также разброс чаевых выше.
pairplot
График pairplot позволяет визуализировать взаимосвязи сразу нескольких количественных переменных. В библиотеке Pandas такой график строится с помощью функции pd.plotting.scatter_matrix().
|
1 2 3 |
# построим pairplot в библиотеке Pandas # в качестве данных возьмем столбцы total_bill и tip датасета tips pd.plotting.scatter_matrix(tips[['total_bill', 'tip']]); |

Как вы видите, там, где перемекаются разные признаки, строится точечная диаграмма, на пересечении одного и того же признака по главной диагонали — его гистограмма.
Примерно такой же график можно построить с помощью функции sns.pairplot() библиотеки Pandas.
|
1 2 |
# параметр height функции pairplot() задает высоту каждого графика в дюймах sns.pairplot(titanic[['Age', 'Fare']].sample(frac = 0.2, random_state = 42), height = 4); |

Обратите внимание на метод .sample() с параметром frac = 0,2, который мы применили к датафрейму titanic. Таким образом, мы сделали случайную выборку из 20% или $ 891 \times 0,2 \approx 178 $ наблюдений.
|
1 2 |
# параметр random_state обеспечивает воспроизводимость результата titanic[['Age', 'Fare']].sample(frac = 0.2, random_state = 42) |

Метод .sample() в данном случае применяется для того, чтобы ускорить создание pairplot. Зачастую, при наличии большого числа наблюдений, график может строиться очень долго.
При добавлении параметра hue (разделение по категориальной переменной) гистограмма по умолчанию превращается в график плотности.
|
1 2 3 4 |
# обратите внимание, столбец Survived мы добавили и в параметр hue и в датафрейм с данными sns.pairplot(titanic[['Age', 'Fare', 'Survived']].sample(frac = 0.2, random_state = 42), hue = 'Survived', height = 4); |

По большому счету с помощью такого графика мы пытаемся ответить на вопрос, есть ли взаимосвязь между возрастом пассажиров и стоимостью их билетов в разрезе выживаемости.
Функция sns.pairplot() является надстройкой (упрощенной версией) другой функции этой библиотеки, sns.PairGrid(). Ее стоит использовать, если требуются более продвинутые настройки графика pairplot.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим объект класса PairGrid, в качестве данных передадим ему # как количественные, так и категориальные переменные g = sns.PairGrid(tips[['total_bill', 'tip', 'time', 'smoker']], # передадим в hue категориальный признак, который мы будем различать цветом hue = 'time', # зададим размер каждого графика height = 5) # метод .map_diag() с параметром sns.histplot выдаст гистограммы на диагонали g.map_diag(sns.histplot) # слева и снизу от диагонали мы выведем точечные диаграммы и зададим # дополнительный категориальный признак smoker с помощью размера точек графика g.map_lower(sns.scatterplot, size = tips['smoker']) # справа и сверху будет график плотности сразу двух количественных признаков g.map_upper(sns.kdeplot) # добавим легенду, adjust_subtitles = True делает текст легенды более аккуратным g.add_legend(title = '', adjust_subtitles = True); |
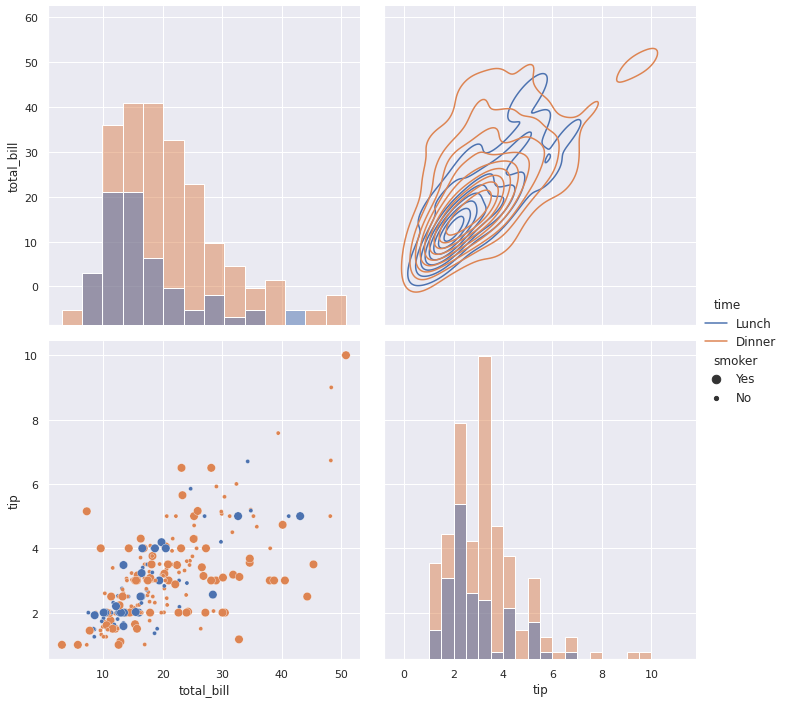
При построении таких сложных графиков важно помнить про их информативность. В примере выше некоторые графики (например, точечную диаграмму) уже достаточно сложно анализировать.
jointplot
Совместное распределение двух переменных
График плотности (kde plot) двух количественных признаков (верхний справа в примере выше) представляет собой визуализацию совместного распределения (joint distribution) двух количественных признаков (tip и total_bill) с разделением по категориальному признаку (time). Другими словами, мы смотрим на то, как изменяется распределение одного количественного признака под воздействием другого. И так для каждой из двух категорий.
В результате мы получаем графики изолиний (contour lines), которые показывают, что между суммой чека и чаевыми есть взаимосвязь (если бы ее не было, изолинии представляли бы собой круги). Теоретические основы совместных распределений мы рассмотрим на курсе по статистике вывода, а пока изучим инструмент их визуализации, который называется jointplot.
sns.jointplot()
Вначале построим точно такой же график плотности (kde plot) совместного распределения tip и total_bill с разделением по признаку time. Для этого функции sns.jointplot() передадим данные и укажем параметр kind = ‘kde’.
|
1 2 3 4 5 6 |
sns.jointplot(data = tips, # передадим данные x = 'total_bill', # пропишем количественные признаки, y = 'tip', hue = 'time', # категориальный признак, kind = 'kde', # тип графика height = 8); # и его размер |
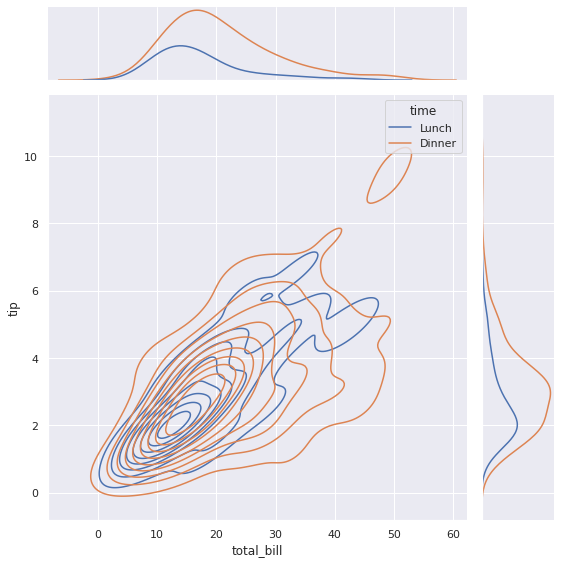
По краям мы видим графики плотности так называемого безусловного распределения (marginal distribution) каждого из признаков. Это одномерные распределения (univariate distribution). Основной график показывает совместное распределение (joint distribution) уже двух переменных. Это двумерное распределение (bivariate distribution).
Возможно более интуитивным покажется использование точечной диаграммы (kind = ‘scatter’) вместо графика плотности.
|
1 2 3 4 5 6 7 8 9 10 11 |
sns.jointplot(data = tips, x = 'total_bill', y = 'tip', hue = 'time', # построим точечную диаграмму kind = 'scatter', # дополнительно укажем размер точек s = 100, # и их прозрачность alpha = 0.7, height = 8); |
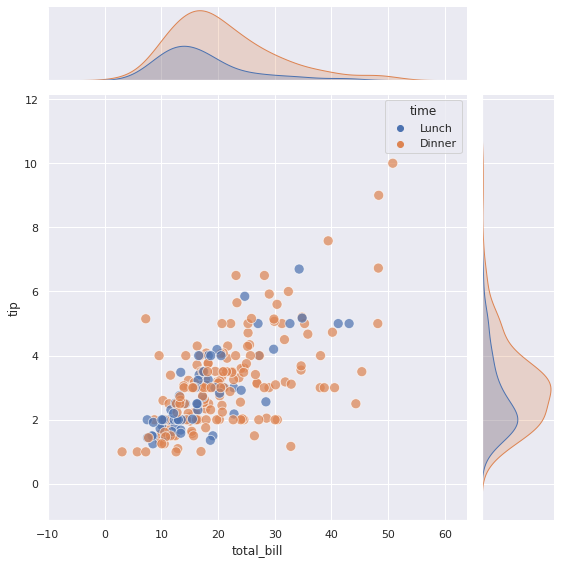
Кроме того, мы можем построить линию регрессии, проходящую через точки. Правда в этом случае придется отказаться от параметра hue, разделять данные на категории и одновременно строить линию регрессии sns.jointplot() не умеет.
|
1 2 3 4 5 6 7 |
# для построения линии регрессии на данных # используем параметр kind = 'reg' sns.jointplot(data = tips, x = 'total_bill', y = 'tip', kind = 'reg', height = 8); |

heatmap
Наконец, если мы хотим вывести какие-либо статистические показатели взаимосвязи двух количественных переменных (например, корреляцию), это можно сделать с помощью чисел. Выведем корреляционную матрицу между total_bill и tip с помощью метода .corr().
|
1 |
tips[['total_bill', 'tip']].corr() |

В следующем разделе мы более подробно поговорим про взаимосвязь переменных в целом и корреляцию в частности.
Или с помощью цвета. Во втором случае мы будем строить то, что называется тепловой картой (heatmap). Поместим созданную выше корреляционную матрицу в функцию sns.heatmap().
|
1 2 3 4 5 |
sns.heatmap(tips[['total_bill', 'tip']].corr(), # дополнительно пропишем цветовую гамму cmap= 'coolwarm', # и зададим диапазон от -1 до 1 vmin = -1, vmax = 1); |

Более насыщенный красный цвет (верхняя граница шкалы) демонстрирует корреляцию признака с самим собой, менее насыщенный — достаточно сильную положительную корреляцию признаков.
Сравнение датасетов
Рассмотрим еще одну библиотеку, которая позволяет не просто сравнивать количественные и качественные переменные в датасете, а сразу сравнивать два датасета. Зачастую, сравнение двух датасетов имеет смысл, когда перед нами обучающая и тестовая выборки.
Скачаем и подгрузим в сессионное хранилище тестовую часть датасета «Титаник».
Библиотека Sweetviz
Теперь установим и импортируем библиотеку sweetviz.
|
1 |
!pip install sweetviz |
|
1 |
import sweetviz as sv |
Импортируем обучающую и тестовую выборки.
|
1 2 |
train = pd.read_csv('/content/train.csv') test = pd.read_csv('/content/test.csv') |
Передадим оба датасета в функцию sv.compare(). Эта функция создаст объект DataframeReport, к которому мы сможем применить метод .show_notebook() для выведения результата.
|
1 |
comparison = sv.compare(train, test) |

|
1 2 |
# посмотрим на тип созданного объекта type(comparison) |
|
1 |
sweetviz.dataframe_report.DataframeReport |
|
1 2 |
# применим метод .show_notebook() comparison.show_notebook() |

Интерактивную версию этого отчета вы найдете в ноутбуке к занятию⧉.
Количественные переменные
По большому счету мы получаем информацию о каждой из переменных в разрезе двух датафреймов. Обратимся к столбцу Age.
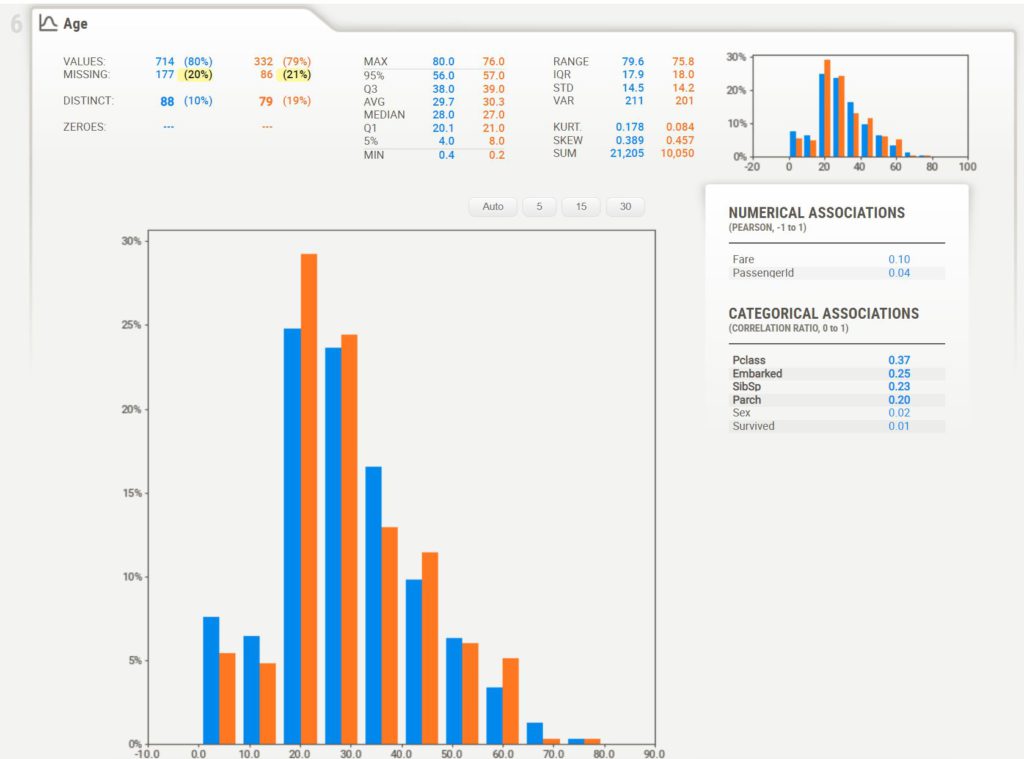
В отчете есть информация о присутствующих (values) и отсутствующих значениях (missing), количестве уникальных (distinct) и нулевых (zeroes) значений. Кроме того, мы видим базовые статистические показатели и гистограмму распределения переменной в каждом из датафреймов.
Отдельно стоит отметить выявление взаимосвязи:
- для двух количественных переменных используется коэффициент корреляции Пирсона (Pearson correlation coefficient); и здесь мы видим, что корреляция возраста со столбцами Fare и PassengerId ожидаемо близка к нулю
- для выявления взаимосвязи между количественной и качественной переменными используется корреляционное отношение (correlation ratio); например, мы видим, что возраст в некоторой степени связан с классом пассажира Pclass
Качественные переменные
Обратимся к столбцу Sex.

В первую очередь отметим, что программа самостоятельно определила, что речь идет именно о категориальном признаке. Для его визуализации была построена столбчатая диаграмма с разбивкой по обучающей и тестовой выборке. Кроме того, мы можем количественно оценить значения в каждой из категорий.
Для поиска же взаимосвязи между двумя категориальными переменными используется коэффициент неопределенности (uncertainty coefficient) или U Тиля, и мы видим некоторую связь с целевой переменной Survived. Для количественной и качественной переменных по-прежнему используется корреляционное отношение.
Более подробную информацию об этой библиотеке можно посмотреть на странице документации⧉.
Перейдем к третьей части занятия.